Lesson 3
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-2 SS |
| Book: | Lesson 3 |
| Printed by: | Guest user |
| Date: | Tuesday, 30 December 2025, 4:01 AM |
Description
Created by IMSreader
1. Lesson 3
Module 1: Trigonometry
Lesson 3: The Cosine Law
Focus

Sean Murphy/Digital Vision/Thinkstock
There are many instances where direct measurement is not possible. If you can create a triangle using values that can be measured, you can often use trigonometry to calculate the value that is needed.
Jennifer and David are designing an obstacle course. They have a number of different tasks that participants need to complete, and they need to figure out what supplies they need to purchase to set up all of the tasks. They are able to directly measure angles and distances for many of the tasks, but some of them aren’t easily measured directly.
For the first task, people will need to hang on to a rope while crossing a rapidly flowing stream that is about 1 m deep. Jennifer and David need to know the distance across the river to be sure that the rope is long enough. They don’t have a tape measure long enough to measure this, so they decide to create a triangle using measurements they can make in order to calculate this value.
David and Jennifer know the measures of the canyon walls and the angle at the bottom, as shown in the following diagram. The rope corresponds to side f.

You will discover as you work through this lesson how David and Jennifer can determine the value of f.
This lesson will help you answer the following inquiry questions:
- What formulas can be used to solve for angles and sides in any triangle (including oblique triangles)?
- How do you determine when to use the sine law and when to use the cosine law?
Assessment
- Lesson 3 Assignment
All assessment items you encounter need to be placed in your course folder.
Save a copy of the Lesson 3 Assignment to your course folder. You will receive more information about how to complete the assignment later in this lesson.
1.1. Discover
Module 1: Trigonometry
Discover
In the previous lesson you learned that the sine law can be used for any triangle, including oblique and right triangles. Although it is true that the sine law can be applied to any triangle, sometimes the information that you are given is not enough to use the sine law.
Consider Jennifer and David’s problem. They have not been given enough information to conclude that their triangle is a right triangle, so they know that they can’t use the primary trigonometric ratios or the Pythagorean theorem. In their math class, they learned that the sine law can be used for any triangle, but they are not sure that they have enough information to use the sine law.
Share 1
Consider the triangle that David and Jennifer created to help them find the length of the rope they need to purchase.
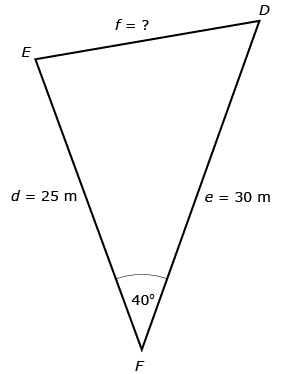
With a partner, write out all three equations of the sine law. Why can’t the sine law be used to find the length of side f?
Recall that the sine law is a compact way of writing the following three equations:
Share 2
Watch the animation titled Jennifer and David’s Solution to see a method for solving the problem.
With a partner, decide what would change if the triangle in Jennifer and David’s problem had the following measurements:
- d = 45 m
- e = 54 m
- ∠F = 57°
You may want to replay the animation.
1.2. Explore
Module 1: Trigonometry
Explore
What Jennifer and David did in their solution was to derive an equation called the cosine law. It’s a “law” because none of the steps relied on specific measurements for sides or angles. As a result, those steps and the final result are valid for any acute triangle. (The cosine law is actually valid for any triangle, including obtuse triangles, but a slightly different derivation is required.)
The cosine law is usually written in the following way:
a2 = b2 + c2 − 2bc cos A
Recall from Lesson 2 that mathematicians typically label sides with lowercase letters and angles with uppercase letters. Furthermore, sides and angles with the same letter are across from each other. For instance, side a is across from ∠A.
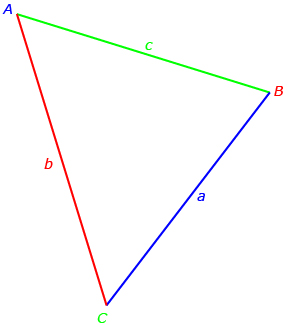
Keep this naming convention in mind. A in the equation must be the measure of the angle across from side a, which is the one you’ll be trying to determine. Look closely at the equation (a2 = b2 + c2 − 2bc cos A). In order to determine the length of one side—a in the equation—you must know the following:
- the lengths of the other two sides (b and c)
- the angle across from the side you’re trying to determine (A)
You can use the Cosine Law Explorer applet to see that the cosine law is valid for any triangle. Drag the vertices of the triangle and confirm that the left side of the cosine law is always equal to the right side.
The animation titled Cosine Law Illustrator may help you better understand the relationships among a, b, c, and ∠A in the cosine law.
1.3. Explore 2
Module 1: Trigonometry
Self-Check 1
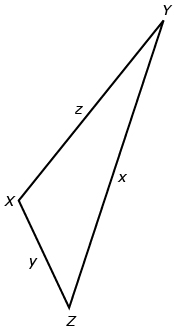
Given the following triangle, state three different ways the cosine law can be written, depending on which angle you are working with.
Example 1
The cosine law can be used to solve the problem given in the Focus section.
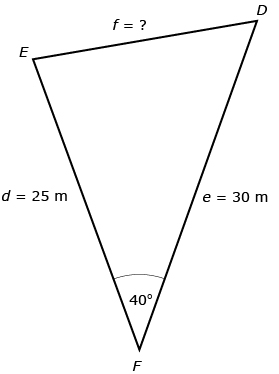
To use the cosine law, you could perform the following steps:
|
f2 = d2 + e2 − 2(d)(e) cos F |
Start by stating the correct cosine law for the question. |
|
f2 = 252 + 302 − 2(25)(30) cos 40° |
Remember that the angle in the equation is the one across from the side you’re trying to determine. In this example, ∠F is across from the side you are trying to determine. |
|
f2 = 375.9333… |
Some students enter the equation above in more than one step (often incorrectly). Remember that your calculator can deal with complicated expressions. Just enter the equation above exactly as you see it. |
|
|
You must use the unrounded answer from the previous step. Many calculators let you do this using the ANS key, which stands for “Answer from previous step.” For some calculators, you would enter |
|
f = 19.3890… |
The unrounded value of f is 19.3890… |
|
f = 19.4 m |
Round the final answer to one decimal place unless instructed otherwise. |
Read “Example 1: Using reasoning to determine the length of a side” on page 146 of your textbook. Notice how Justin analyzed the information provided and concluded that he could use the cosine law.
Ensure that you are comfortable with the steps in this solution before moving on.
1.4. Explore 3
Module 1: Trigonometry
Self-Check 2
Complete the following questions. Be sure to check your answers to ensure that you understand the solution process.
- Complete “Check Your Understanding” question 2 on page 151 of your textbook. Answer
- Complete “Practising” questions 4 and 11 on pages 151 and 152 of your textbook. Answer
The cosine law can also be used to determine angle measures. Because the formula includes one angle, if you are given all three sides, the cosine law can be used to solve for any angle in a triangle.
Read “Emilie’s Solution: Rearranging the cosine law before subtracting” on page 148 of your textbook to see how Emilie rearranges the cosine law formula to isolate cos B. This will make it much easier to find an angle when given all three side lengths.
The rearranged form is
![]()
You know that the cosine law can be written in three ways, depending on which side you are looking for:
- a2 = b2 + c2 − 2bc cos A
- b2 = a2 + c2 − 2ac cos B
- c2 = a2 + b2 − 2ab cos C
The same is true when the formula is rearranged to solve for the cosine of an angle.
1.5. Explore 4
Module 1: Trigonometry
Self-Check 3
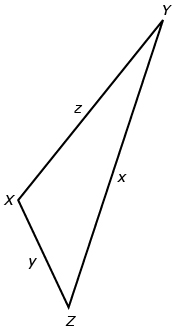
Given the following triangle, state three different ways the cosine law can be written when all three sides are given and you are solving for unknown angles.
Example 2

David De Lossy/Photodisc/Thinkstock
Sandra is taking the same orienteering course as Jeremy in Lesson 2. Sandra is standing at Checkpoint C and knows distances to two other checkpoints, as shown in the diagram. In order to walk in the correct direction, she needs to determine the angle between Checkpoint A and Checkpoint B (θ on the diagram).
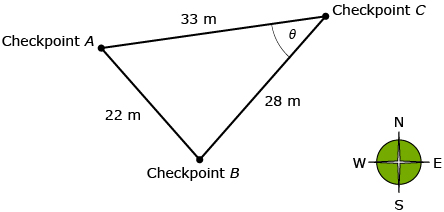
Sandra uses the cosine law to determine angle θ.
|
|
Write a correct version of the formula. |
|
|
For this problem, angle θ is across from the side that is 22 m long. Sandra replaces C in the formula with θ because that’s how it’s labelled in her diagram. |
|
cos θ = 0.7516… |
Caution: When entering fractions on a calculator, extra care must be taken with brackets. The easiest approach is to always put the numerator in brackets and the denominator in brackets. For this example, you would enter the following in your calculator: |
|
θ = cos−1(0.7516…) |
Use inverse cosine (cos−1) to determine θ. |
|
θ = 41.2688…° |
The unrounded value of θ is 41.2688…° |
|
θ = 41° |
Remember to round to the nearest degree unless instructed otherwise. |
1.6. Explore 5
Module 1: Trigonometry
Self-Check 4
Complete the following questions. Be sure to check your answers carefully to ensure that you understand the solution process. If you are still having trouble, contact your teacher.
- Complete “Check Your Understanding” question 3 on page 151 of your textbook. Answer
- Complete “Practising” questions 5 and 8 on pages 151 and 152 of your textbook. Answer
In this lesson you have learned when you can use the sine law and when you can use the cosine law. If you haven’t done so already, go to your course folder and update your notes organizer with any thoughts or key ideas about these two laws. For instance, you might find it helpful to draw a picture showing an example of the sine law and another picture showing an example of the cosine law. Remember to save your updated notes organizer to your course folder.
You may also want to add both forms of the cosine law to your Formula Sheet document. Save the Formula Sheet document to your course folder.
1.8. Lesson 3 Summary
Module 1: Trigonometry
Lesson 3 Summary
In this lesson you learned that although the sine law is valid for all triangles, sometimes the information that you are given is not enough to use the sine law.
You also learned the cosine law, which is valid for all triangles (just like the sine law):
a2 = b2 + c2 − 2bc cos A
![]()
When deciding whether to use the sine law or the cosine law, consider which values are given and which values you need to find. If you have a side-angle pair (i.e., one side and its opposite angle), then you can use the sine law. If you do not have a side-angle pair, then you will likely need to use the cosine law.
In the next lesson you will apply what you have learned about the sine and cosine laws to problems involving more than one triangle.