Lesson 4
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-2 SS |
| Book: | Lesson 4 |
| Printed by: | Guest user |
| Date: | Saturday, 6 September 2025, 2:32 AM |
Description
Created by IMSreader
1. Lesson 4
Module 1: Trigonometry
Lesson 4: Working with Multiple Oblique Triangles
Focus
iStockphoto/Thinkstock
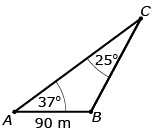
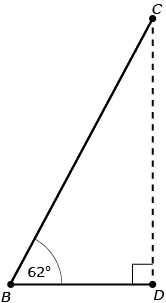
Joey is flying a kite and wants to determine its height. He enlists the help of his friend, Jahnavi, who is standing 90 m away. Joey uses a clinometer and determines that the angle of elevation to the kite is 62°. Jahnavi determines that the angle of elevation is 37°.
There are multiple triangles in this diagram, and one of them is oblique. Should you use the primary trigonometric ratios? Should you use the sine law or the cosine law?
In Lesson 1 you solved problems involving multiple right triangles. In the last two lessons you learned how to solve problems involving oblique triangles. In this lesson you will combine these skills to help you decide whether the primary trigonometric ratios, sine law or cosine law, should be used to solve problems involving multiple oblique triangles. Solving problems involving multiple oblique triangles is at the heart of triangulation, which you will do in the Module 1 Project.
This lesson will help you answer the following inquiry question:
- How do you determine when to use the sine law and when to use the cosine law?
Assessment
- Lesson 4 Assignment
- Module 1 Project
All assessment items you encounter need to be placed in your course folder.
Save a copy of the Lesson 4 Assignment to your course folder. You will receive more information about how to complete the assignment later in this lesson.
1.1. Discover
Module 1: Trigonometry
Discover
Sometimes it’s hard to choose which trigonometric formula to use. In the following activity you will consider what to look for when you need to choose a formula.
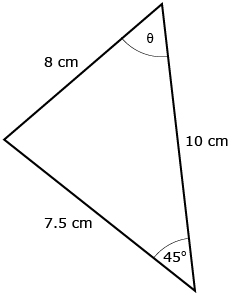
Igor has decided that he can use the sine law to solve for length x:
Igor said he chose the sine law because it uses two sides and two angles. In order to solve an equation, there can be only one unknown quantity. For this triangle, three of the four needed values are known.
Igor is correct. Use the sine law when you know a side-angle pair (e.g., side a and ∠A) and another side or angle.
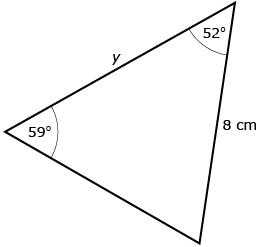
For the next problem, Igor decides to use the sine law to solve for length y. He says, “In the previous diagram, I used the sine law because I knew three measurements in the triangle. I know three measurements for this second triangle, so I can also use the sine law for this problem.” Igor wrote the following equation:
Ronitra says that Igor is not using the sine law correctly.
Share 1
With a partner, complete the following:
- Discuss whether Igor or Ronitra is correct, and justify your opinion.
- Summarize your discussion.
- Describe the conditions for using the sine law to solve a triangle problem.
1.2. Discover 2
Module 1: Trigonometry
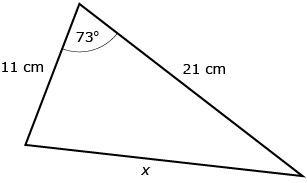
To solve for the length of x in the following triangle, Igor wrote the following equation:
x2 = 212 + 112 − 2(21)(11) cos 73°
Igor said this is valid because the cosine law has three sides and an angle, and, in order to use an equation, you must know all but one of these quantities. Three quantities are known in the triangle.
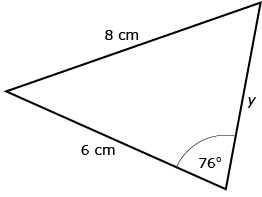
Igor has decided to also use the cosine law to solve for length y. He says, “In the previous problem, I used the cosine law because I knew three of the four quantities in the equation. I know three of the four quantities in this problem, so I can also use the cosine law here as well.” Igor wrote the following equation:
y2 = 82 + 62 − 2(8)(6) cos 76°
Ronitra says that Igor is not using the cosine law correctly.
Share 2
With a partner, complete the following:
- Discuss whether Igor or Ronitra is correct.
- Summarize your discussion.
- Describe the conditions for using the cosine law to solve a triangle problem.
1.4. Explore
Module 1: Trigonometry
Explore
In this lesson you will use your experience to determine whether to use the sine law or the cosine law to solve problems that require more than one triangle. Problems may include right triangles, oblique triangles, or both.
The first problem in the Focus section will now be revisited.
Example 1
Joey is flying a kite and wants to determine its height. He enlists the help of his friend, Jahnavi, who is standing 90 m away. Joey uses a clinometer and determines that the angle of elevation to the kite is 62°. Jahnavi determines that the angle of elevation is 37°. To keep calculations simple for this question, ignore Joey’s height and assume that the kite string touches the ground.
Jahnavi starts by drawing the following diagram.
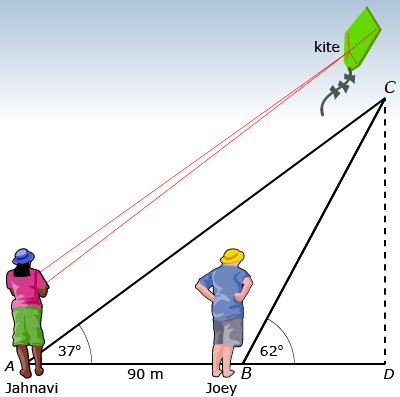
After drawing the picture, Jahnavi realized there are three triangles in this diagram: 
, 
, and 
. Since 
and 
share side BC, she decided to use a three-step approach:
Step 1: She will use her knowledge of straight angles and sums of angles in triangles to determine ∠ABC and ∠ACB.
Step 2: Use 
to determine the length of BC.
Step 3: Use 
to determine the height (CD).
|
Step 1 of Jahnavi’s Solution |
|
|
∠ABC + 62° = 180°
∠ABC = 118° |
Straight angles add to 180°. |
|
37° + 118° + ∠ACB = 180°
∠ACB = 25° |
The sum of the angles in any triangle is 180°. |
|
Step 2 of Jahnavi’s Solution |
|
|
|
|
|
|
Jahnavi multiplied both sides of the equation by sin 37° in order to isolate BC. |
|
BC = 128.1614… |
Jahnavi has not rounded this number because it is not the final answer. |
is not a right triangle, thus the primary trigonometric ratios cannot be used. Jahnavi has chosen to use the sine law. 
|
Step 3 of Jahnavi’s Solution |
|
|
|
|
|
CD = (128.1614… sin 62° |
Multiply both sides of the previous equation by 128.1614… |
|
CD = 113.1598 m |
The unrounded value of CD is 113.1598 m. |
|
CD = 113.2 m |
The kite is 113.2 m above the ground. |
is a right triangle, thus Jahnavi can use SOH CAH TOA.
1.5. Explore 2
Module 1: Trigonometry
Example 2
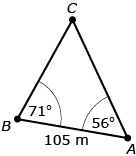
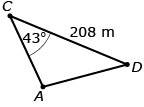
Jeremy is on the third day of his orienteering course and has been asked to determine the distance from point A to point D. He knows some distances and angles as shown in the following diagram.
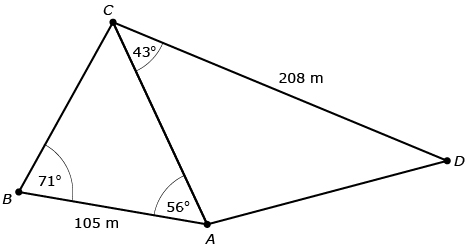
Jeremy noted that 
and 
share side AC. As a result, he can use 
to solve for side AC; and then he can use 
to solve for length AD.
|
Step 1 of Jeremy’s Solution |
|
|
∠BCA = 53° |
Jeremy knows that the sum of the angles in a triangle is 180° and uses that to calculate the measure of ∠BCA. |
|
|
|
|
|
Jeremy multiplied both sides of the equation by sin 71° in order to isolate AC. |
|
AC = 124.3113… |
The unrounded value of AC is 124.3113… |
is not a right triangle. Jeremy chooses to use the sine law to calculate AC.
|
Step 2 of Jeremy’s Solution |
|
|
AD2 = AC2 + 2082 − 2(AC)(208) cos 43° |
Jeremy applies the cosine law to |
|
AD2 = (124.3113…)2 + 2082 − 2(124.3113…)(208) cos 43° |
Jeremy uses the unrounded value for AC by pressing the ANS key on his calculator. |
|
AD2 = 20 896.4368… |
The unrounded value of AD2 is 20 896.4368… |
|
|
Take the square root of both sides to solve for AD. |
|
AD = 144.5559… |
The unrounded value of AD is 144.5559… |
|
AD = 144.6 m |
The distance from point A to D is 144.6 m. |
using AC calculated in step 1. 
Did You Know?
Canada’s First Nations people were the first map makers in Canada. Undoubtedly, their maps were useful to the European explorers of the 1400s. However, these maps had two significant differences to what the Europeans would have been used to using:
- First Nations’ maps were usually memorized and only drawn when required to communicate locations and distances with others.
- The scale of the maps often corresponded to travel time rather than absolute distances. As a result, two identical real-world distances would not be identical on the map if one required more travel time due to rough terrain.
Read “Example 3: Solving a three-dimensional problem” on page 159 of your textbook. Notice how Diana breaks the problem’s solution into two steps—in the first step, she uses the sine law to determine the length of side BC. In the second step, she uses the tangent ratio to determine the height of the cliff.
Ensure that you are comfortable with the steps in this solution before moving on.
1.6. Explore 3
Module 1: Trigonometry
Self-Check 2
Complete the following questions. It is very important that you show all of your work so your teacher can see how you solved the problem. You will have noticed that your answer may be slightly different depending on your solution method. If you don’t show your solution method, it is difficult to determine whether you understand how to solve multiple triangle problems.
- Complete “Practising” question 9 on page 162 of your textbook. Answer
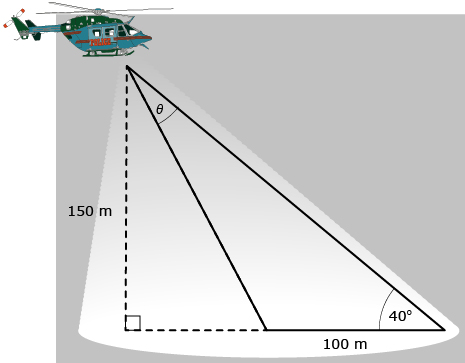
- A police helicopter uses a spotlight to look for suspicious activity at night. One particular night, the helicopter is flying 150 m above the ground and the diameter of the illuminated area is 100 m. Adrian is standing on the ground at the far end of the illuminated area and determines that the angle of elevation to the helicopter is 40°. Adrian has been asked to determine the angular width of the spotlight, marked by θ on the following diagram.
1.7. Connect
Module 1: Trigonometry
Connect
Lesson Assignment
Go to the Lesson 4 Assignment that you saved to your course folder. Complete the questions.
Project Connection
You have almost completed Module 1. In the Module 1 Project you will use the skills that you have learned to solve triangulation problems.
1.8. Lesson 4 Summary
Module 1: Trigonometry
Lesson 4 Summary
In this lesson you examined when each formula is appropriate.
You learned that the sine law is appropriate when
- there is only one unknown in your sine law equation
- you have correctly paired sides and angles (i.e., the side-angle pair for each fraction must be across from each other)
You also learned that it is appropriate to use the cosine law when
- there is only one unknown in your cosine law equation
- you have correctly paired side a and angle A (i.e., they must be across from each other)