Lesson 1
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-2 SS |
| Book: | Lesson 1 |
| Printed by: | Guest user |
| Date: | Tuesday, 30 December 2025, 9:49 AM |
Description
Created by IMSreader
1. Lesson 1
Module 2: Logic and Geometry
Lesson 1: Strategy in Games, Puzzles, and Patterns
Focus
Have you ever noticed how two people can be playing the same game but have two completely different strategies? Understanding your opponent’s strategy is very important in games like chess or role playing games. In these types of games, the success of your next move is dependent on your opponent’s move.

Photodisc/Thinkstock
Understanding strategy can also help to improve your success with one-player games or puzzles. You probably already adapt your strategy based on what works and what doesn’t work. This is part of becoming a better player whether you are playing against yourself, a real opponent, or a virtual opponent.
In this lesson you will investigate how different strategies can be used to find solutions to a puzzle or for winning a game.
This lesson will help you answer the following inquiry question:
- How can different personal strategies be used to solve a puzzle or win a game?
Assessment
All assessment items you encounter need to be placed in your course folder.
While you will not be handing in any work from Lesson 1 for marking, the activities in this lesson will prepare you for other assignments in this module. This lesson provides you with opportunities to investigate, discuss, and practise the knowledge and skills you are learning. For instance, in Try This and Share, you can check your answers with other students to see if you are on track. If you are having difficulty with concepts or calculations, contact your teacher.
For those items that you will not be handing in for marking, you should have already had a discussion with your teacher about how you can access the solutions to these questions. Make sure to follow your teacher’s instructions.
Materials and Equipment
- 10 coins of one denomination (pennies, nickels, dimes, quarters, loonies, or toonies)
- favourite game
Time
Each module is made up of lessons. Each lesson in Mathematics 20-2 is designed to be completed in approximately 80 minutes. You may find that you require more or less time to complete different lessons depending on your strengths. It is important that you progress at your own pace based on your individual learning requirements.
1.1. Discover
Module 2: Logic and Geometry
Discover

iStockphoto/Thinkstock
Strategies for solving a puzzle or winning a game can be quite different. One strategy is not necessarily better than the other. Each strategy has its own strengths and weaknesses. In fact, participants may change their strategy several times throughout a game based on their own or an opponent’s performance.
Try This 1
You should place your completed Try This activities in your course folder. Your teacher may ask to see your completed Try This activities. For more information on Try This activities, refer to the Course Introduction.
Arrange 10 coins to create a triangle as shown in the diagram. Alternatively, you can use the Triangle of Coins applet.
- Manipulate the coins one by one to turn the triangle upside down so the point faces down.
- What is the minimum number of moves to flip the triangle upside down?
Place a description or sketch of your strategy in your course folder. In your sketch, be sure to identify which coins you moved and where you moved them to. You may want to use arrows to identify specific movements or take a video of your manipulations of the coins.
Share 1
After a discussion with your teacher, you will decide how to connect with other students for Share activities. Follow your teacher’s instructions to complete this Share activity. Place a summary of your Share discussion in your course folder. For more information on Share discussions, refer to the Course Introduction.
Compare your strategy for flipping the triangle of coins with another student or partner. This may be done in person or virtually. For instance, you may want to post your response to the discussion board or have a video conference with another student.
In your discussion answer the following questions:
- How were the strategies similar?
- How were the strategies different?
- Were both strategies successful? In other words, was the final orientation a triangle that pointed downwards?
- Who had the lowest number of moves to flip the triangle?
When you compared your strategies for flipping the triangle of coins, did you determine that the minimum number of moves required is three? If not, you may want to go back and revisit your approach.
In the triangle puzzle, a strategy that took three moves would be more successful than a strategy that took five moves. The success of a strategy in this case is based on the number of moves required to complete the puzzle. For some games and puzzles, the number of moves is not crucial. What is important is solving the puzzle. This can be achieved using various strategies.
1.2. Discover 2
Module 2: Logic and Geometry
Try This 2
Use the following information to answer Try This 2.
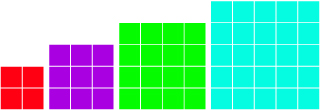
- Use a personal strategy to determine the number of squares in each of the following figures. For example, the 2 × 2 grid has 5 squares and the 5 × 5 grid contains 55 squares. You may find it helpful to organize your answers in a table or list like the one shown.

Grid Size 2 × 2 3 × 3 4 × 4 5 × 5 Number of Squares 5 55
personal strategy: an individual approach to a situation or problem using words or mathematical processes
Developing a personal strategy involves thinking about the situation or problem, planning how to solve the problem or situation, carrying out the plan, and, finally, evaluating the solution. The key is to be creative. Use diagrams, look for patterns, and don’t be afraid to try.
-
Once you have determined the number of squares in each grid, find a pattern that exists between the figure and the number of squares in each figure.

-
Identify how many squares would be in a 10 × 10 grid. Place a copy of your solution in your course folder. In your solution, include the following items:
- Complete a table or list identifying the number of squares in the figures. (Include a 10 × 10 grid in your answers.)
- Identify the pattern you think exists between the figure and number of squares in each figure using a statement.
- Explain the strategy used and why you chose that strategy. (In other words, did you change your strategy as the number of squares increased? Why or why not?)
- Complete a table or list identifying the number of squares in the figures. (Include a 10 × 10 grid in your answers.)
Share 2

Stockbyte/Thinkstock
With a partner, compare your results and discuss your personal strategy for identifying the number of squares in each figure. Summarize your discussions by answering the following questions.
- Explain your strategy to your partner. Did your partner use a different strategy?
-
Were your results the same for each figure and the overall pattern?
- If not, work together to determine the number of squares and the pattern. Revise your statement from Try This 2 to reflect your new pattern, if required.
- You may find it helpful to talk to other students as well about how they identified the pattern.
- If not, work together to determine the number of squares and the pattern. Revise your statement from Try This 2 to reflect your new pattern, if required.
-
Is there any part of your partner’s strategy that you could add or adapt to the approach you used to solve the puzzle?
Recall from the Course Introduction that you will be creating your own glossary. You have a couple of options. You may open and start a new Glossary Terms document now and add any new terms. Or, if you started a Glossary Terms document in Module 1 and saved it to your course folder, you may wish to continue adding new terms to this existing document and resave it to your course folder.
1.3. Discover 3
Module 2: Logic and Geometry
Many games and puzzles have histories that go back decades or even centuries. For example, the Rubik’s Cube was created by Hungarian architect, designer, and university professor Ernõ Rubik in the 1970s. The first version of the cube was called the Magic Cube and began selling in Budapest in 1977.1
Rubik didn’t set out to create the world’s best-selling toy. He wanted a working model to help explain three-dimensional geometry and ended up creating a toy that has sold more than 300-million copies.2

Hemera/Thinkstock
Did You Know?
A standard Rubik’s Cube is made up of six coloured sides, twenty-one pieces, and fifty-four individual coloured squares. There are more than 43-quintillion
(43 000 000 000 000 000 000) possible configurations but only one solution.3 For the exact number of configurations, type “Rubik’s Cube Math” into your favourite search engine.
As time passes and technologies improve, the way games and puzzles are presented and played is changing. Today, you can download an application and play Rubik’s Cube or thousands of other games and puzzles right on your mobile phone or computer.
Share 3
Present your favourite game to a classmate or other appropriate partner. This may be a board game, a game on your favourite gaming system, an online game, or a game or puzzle on your cellphone. Alternatively, you may choose to find a new game or puzzle to explore.
In your explanation of the game or puzzle, tell your partner the following information:
- what you like about the game
- the goal of the game
- how the game is played
If possible, allow your partner to play the game. Then, discuss your personal strategies for winning or completing the game. Include the following questions in your discussion:
- How do your strategies compare?
- Is there any part of your partner’s strategy that you could use to help your performance?
1, 2, 3 Rubik’s Cube (R) used by permission of Seven Towns Ltd. www.rubiks.com
1.4. Lesson 1 Summary
Module 2: Logic and Geometry

iStockphoto/Bonnie Jacobs/Thinkstock
Lesson 1 Summary
Different strategies can be used to solve puzzles and win games. Knowing your personal strategy and being able to adapt your strategy as required can help you improve your success with games or puzzles. Sharing your approach is another way to gain useful information. An opponent or fellow teammate may have a different way of approaching the game or puzzle. You may choose to incorporate all, part, or none of the other person’s strategy into your game play.
In the next lesson you will continue to investigate how reasoning can be used to help develop winning strategies.