Lesson 2
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-2 SS |
| Book: | Lesson 2 |
| Printed by: | Guest user |
| Date: | Tuesday, 30 December 2025, 9:46 AM |
Description
Created by IMSreader
1. Lesson 2
Module 2: Logic and Geometry
Lesson 2: Conjectures and Inductive Reasoning
Focus
Winning a game or solving a puzzle involves looking for patterns. These patterns may be numerical, like the pattern in the squares activity in Lesson 1. Patterns may also be spatial, like in the triangle puzzle you investigated.
© 2011 Royal Canadian Mint – All Rights Reserved.
In Lesson 1 you developed personal strategies to solve puzzles or win games. You may have used logic or reasoning to identify patterns or moves that helped you to be successful. As you worked through the puzzles or games, did you find that you had to adapt your strategy because of your opponent’s approach or other changing conditions in the game? Did you have to develop a new approach or revise your original strategy because the pattern you identified was incorrect?
In this lesson you will continue to investigate how reasoning can be used to make predictions or generalizations. The role of reasoning in developing a personal strategy and what happens when a generalization is shown to be false will also be explored.
This lesson will help you answer the following inquiry questions:
- How can reasoning be used to make predictions or generalizations?
- How can a prediction be invalidated?
Assessment
- Lesson 2 Assignment
All assessment items you encounter need to be placed in your course folder. You should have already had a discussion with your teacher about which items you will be handing in for marking. For those items you will not be handing in for marking, you should have already had a discussion with your teacher about how you can access the solutions to these questions. Make sure you follow your teacher’s instructions.
Save a copy of the Lesson 2 Assignment to your course folder. You will receive more information about how to complete the assignment later in this lesson.
Materials and Equipment
- two decks of cards
1.1. Explore
Module 2: Logic and Geometry
Explore
conjecture: a conclusion, a generalization, or an educated guess that is based on available evidence but is not yet proved
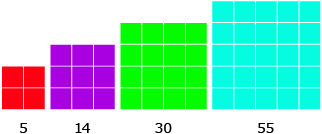
In Lesson 1 you used the information you were given to discover a pattern in a set of square figures. You then wrote a statement identifying the pattern you determined. For example, you may have stated that the 10 × 10 grid would have 385 squares, which is the sum of the first 10 perfect squares. This is an example of a conjecture.

computer: iStockphoto/Thinkstock
![]()
A perfect square is a number that can be expressed as the square of another number. The numbers 1, 4, 9, 16, 25, 36, and 49 are all perfect squares.
1 × 1 = 1
2 × 2 = 4
3 × 3 = 9
4 × 4 = 16
5 × 5 = 25
6 × 6 = 36
7 × 7 = 49
You developed your conjecture about the number of squares by observing the pattern in the figures. In other words, you used inductive reasoning to develop your conjecture. Inductive reasoning uses specific cases to put together a more general conclusion. For instance, in the squares activity from Lesson 1, your conjecture may have been based on the number of squares in the 2 × 2 grid, the 3 × 3 grid, the 4 × 4 grid, the 5 × 5 grid, and the 10 × 10 grid. You might even have looked at the number of squares in a 6 × 6 grid or an 8 × 8 grid to help establish the pattern. Since it would be very difficult, if not impossible, to look at the number of squares in every possible size of grid, your conjecture of the pattern is based on inductive reasoning.
![]()
inductive reasoning: a type of reasoning used to draw a general conclusion based on experience, observations, or patterns in specific examples
1.2. Explore 2
Module 2: Logic and Geometry
Read “Example 1: Using inductive reasoning to make a conjecture about annual precipitation” on pages 7 and 8 of your Principles of Mathematics 11 textbook.
Share 1
With a partner, discuss the following questions regarding Lila’s solution from “Example 1” shown in the textbook.
- How did Lila come up with her conjecture?
- Does Lila’s reasoning make sense to you?
- How did Lila check whether the data supported her conjecture?
- What other conjectures could be made based on the patterns in the precipitation chart?
Self-Check 1
- Read “Example 2: Using inductive reasoning to develop a conjecture about integers” on page 8 of your textbook. Then complete “Your Turn” following Example 2 on page 8 of your textbook. Answer
- Complete “Practising” question 9 on page 13 of your textbook. Answer
Different personal strategies can be used to gather information to develop a conjecture about a given situation. For instance, a geometric or numeric approach may be used to identify a pattern.
In “Example 3: Using inductive reasoning to develop a conjecture about perfect squares” on page 9 of your textbook, two students make two different conjectures about the difference between consecutive perfect squares. Before turning to page 9 to read the solutions, view the following animations that showcase each student’s approach.
After viewing the animations, you can read about each student’s solution on page 9 of your textbook.
A prime number is a natural number that has exactly two factors: 1 and itself. The numbers 2, 3, 5, 7, 29, 31, 43, and 89 are examples of prime numbers.
For more information on prime numbers or to check whether a number is prime or not, refer to Prime Number.
1.3. Explore 3
Module 2: Logic and Geometry
Share 2
After investigating Steffan’s and Francesca’s personal strategies, discuss the following questions with your partner:
- How is it possible to have two different conjectures about the same situation?
- What strategies were used by Steffan and by Francesca to gather the evidence?
- What patterns did Steffan and Francesca find that they then used to develop their conjectures?
- Which conjecture do you prefer? Explain why.
Francesca and Steffan were both investigating the same situation, but the strategies they used to develop their conjectures were different. The common feature or property Steffan identified in his examples (i.e., odd numbers) was different than the common property Francesca found in her examples (i.e., prime numbers). So they ended up with two different conjectures about the same situation.

This example shows that it is possible to have different conjectures developed based on the following:
- method of observation
- samples or examples used
- interpretation of the evidence
Both Steffan and Francesca made general conclusions based on specific examples. Their conjectures were based on and supported by the specific examples they chose to use. So how can you determine whether their conjectures are reasonable or valid? Or how can you determine whether one conjecture is stronger than the other?
A conjecture can be strengthened by finding more examples that support it. The more support for a conjecture, the stronger or more reasonable the conjecture. Likewise, the selection of examples can affect the strength of a conjecture. Choosing only one type of example to support your conjecture limits the strength and reasonableness of the conjecture.
Did You Know?

iStockphoto/Thinkstock
The Clay Mathematics Institute of Cambridge, Massachusetts, established seven Millennium Prize Problems in the year 2000. The problems are based on conjectures made by mathematicians over the past few hundred years. The prize for solving one of these problems is US$1 million.
Dr. Grigoriy Perelman was awarded the first Clay Mathematics Institute Millennium Prize on March 18, 2010, for resolving the Poincaré conjecture. French mathematician Henri Poincaré developed the conjecture in 1904.
Want to take a shot at solving these problems and winning a million dollars? Type the keywords “CMI Millennium Prize” using your favourite Internet search engine.
Did You Know?

The great mathematician Leonhard Euler (1707–1783) made a conjecture based on a variation of Fermat’s Last Theorem. For over 200 years, the conjecture looked like it was true. Then, the conjecture was disproved. It failed on the number 61 917 364 224.
Mathematicians need to know that there will never be a counterexample to their conjecture. Just checking examples is never enough to prove a conjecture. For every example you check, there could be one that could fail the test.
Read “Example 2: Connecting to previous conjectures” on pages 19 and 20 of your Principles of Mathematics 11 textbook. As you read, consider whether
- more trials strengthen Steffan’s and Francesca’s conjectures
- it is possible to disprove a conjecture and, if so, what has to happen for a conjecture to be disproven
- more trials can prove a conjecture
More support for a conjecture developed through inductive reasoning will strengthen the conjecture but does not prove it. Even if a counterexample is not found, it does not mean that the conjecture is true. It is not possible to try all the possible cases, so it is not possible to prove a conjecture. On the other hand, one counterexample can disprove a conjecture. Once a counterexample has been found, the conjecture is invalid.
counterexample: an example that invalidates or shows a conjecture to be false
If it is easy to find a counterexample to a conjecture, then the conjecture is very weak. To strengthen the conjecture, it is important to test the conjecture to try to find counterexamples. Sometimes, a conjecture is made that seems obvious; but once you do a little testing, you quickly find a counterexample to disprove it. In this case, you may ask yourself, “Was I completely wrong? Is there any truth to my original conjecture?”
1.4. Explore 4
Module 2: Logic and Geometry

PhotoObjects.net/Thinkstock
Try This 1
Vicky is working on a design for a quilted circular pillow. In her design, she is marking points on the circumference of the circle and then joining the points with line segments ![]() or chords
or chords ![]() to create regions. She is trying to determine how many different types of fabric she will need to cover the pillow top if each region is to be a different colour or pattern of fabric.
to create regions. She is trying to determine how many different types of fabric she will need to cover the pillow top if each region is to be a different colour or pattern of fabric.
As she is drawing her sketch of the circular pillow design, she notices the pattern shown in the following sketch.
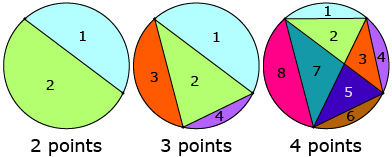
- Based on Vicky’s sketch, make a conjecture about the relationship between the numbers of regions created within the circle and the number of points on the circumference of the circle.
- Use the Circle Conjecture applet to test the validity of your conjecture. As you test the conjecture, consider the following questions:
Share 3
Share your findings from Try This 1 with another student or appropriate partner either in person or virtually. Use the following questions to guide your discussion.
- Explain the conjecture you developed for the relationship between the number of regions created within the circle and the number of points on the circumference of the circle.
- Present your opinion on the amount of examples or evidence required to test the conjecture. How does it compare with your partner's opinion?
- Identify a counterexample, if applicable. What does this tell you about your conjecture?
1.5. Explore 5
Module 2: Logic and Geometry
In Lesson 1 you may have found that you had to adapt or revise your personal strategy for winning a game if your original strategy was not successful. In a similar manner, counterexamples tell us that a conjecture or strategy was not successful. When a counterexample is found, a conjecture may be revised or changed to limit it.
For instance, Vicky had made the following conjecture based on her pillow sketch.
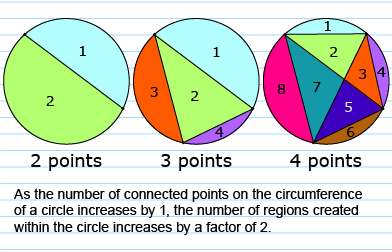
Vicky’s conjecture is valid for 5 or less points. A counterexample was found for 6 points. This showed that the conjecture was false once there were 6 or more points on the circle. Vicky could revise her conjecture by limiting it to 5 or less points on the circumference of the circle.
If you want to see another example of using reasoning to find a counterexample to a conjecture, read “Example 3: Using reasoning to find a counterexample to a conjecture” on page 21 of your textbook.
In 1959, Arthur L. Samuel of the IBM research department programmed an IBM 704 computer to play a fair game of checkers with an opponent. The computer was capable of looking over its past games and modifying its strategy based on its experiences. It was one of the first learning machines that could steadily improve its ability to play games.
— Martin Gardner. The Colossal Book of Mathematics. (New York: W. W. Norton, 2001), pp. 471-472.
The process of making a conjecture and then revising it based on new information is characteristic of inductive reasoning. The following Try This activity provides you with an opportunity to play a game and make conjectures. Your conjectures can then be adapted based on the evidence you collect as the game progresses.
If you do not have the opportunity for group activities, you can use the Self-Check questions presented after Try This 2 to verify your understanding of inductive reasoning. Check with your teacher about what piece or pieces you should complete—the Try This 2 and/or the Self-Check 2 questions.
Try This 2
Play the I Like Game. Read over the instructions before playing this game with a partner or with a group.
After you have played a few rounds of the game, answer the following: How does the game model inductive reasoning?
In your response, identify how conjectures were used. Also, describe how finding a counterexample changed your strategy or revised your original conjecture.
Self-Check 2
Remember to check with your teacher about whether you are to complete Try This 2 and/or the Self-Check 2 questions for this portion of the lesson.
Complete “Further Your Understanding” question 2 on page 17 of your textbook. Answer
1.6. Connect
Module 2: Logic and Geometry
Connect
Lesson Assignment
Complete the Lesson 2 Assignment that you saved to your course folder now.
As you complete this assignment, you may wish to answer electronically. To learn how to insert equations into a Word document, such as your lesson assignment, watch the video Inserting Equations in MS Word 2007. The video Inserting Shapes in MS Word 2007 shows how to insert shapes into a Word document.
1.7. Lesson 2 Summary
Module 2: Logic and Geometry
Lesson 2 Summary

Hemera/Thinkstock
Every day, people make predictions and generalizations based on patterns. They may make observations of a pattern while playing a game, solving a puzzle, or while watching a particular situation. When specific observations are used to make general conclusions or conjectures about a situation, inductive reasoning is being used.
![]()
For instance, an adult couple that observes a few video game stores full of teens may make the statement that all teens like video games. Their conjecture is based on observations of the clientele in video game stores. The conjecture may be strengthened by observations of more teens playing video games or other game stores full of teens.
As you have seen in Lesson 2, the more evidence gathered to support a conjecture, the stronger the conjecture. The conjecture can be invalidated by finding one counterexample: it is possible to find one teen that doesn’t like video games. Because it is impossible to ask all teens whether they like video games, it is not possible to prove the conjecture “all teens like video games.”
Conjectures can be revised based on new evidence or counterexamples. Adapting conjectures based on observations is one way of revising strategies for successfully winning a game or solving a puzzle.
In Lesson 3 you will investigate what has to happen to prove a conjecture.