Lesson 3
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-2 SS |
| Book: | Lesson 3 |
| Printed by: | Guest user |
| Date: | Tuesday, 30 December 2025, 9:47 AM |
Description
Created by IMSreader
1. Lesson 3
Module 2: Logic and Geometry
Lesson 3: Proving Conjectures

Focus
Magicians frequently amaze their audience with their ability to guess which card a participant has picked from a deck of cards. Can magicians really read minds? Or is the guess a result of some other trick of the trade?
Perhaps the deck of cards is only made up of a few different cards like the 2 of spades and 2 of diamonds. This is called a stacked deck because it greatly decreases the number of possible cards the participant may have chosen. By asking questions like “Is your card red?” the magician can use reasoning to make conjectures and ultimately determine which card the participant is holding.
A lot of different games can be solved using logical reasoning. Logic games and number tricks are examples of games where reasoning plays an important role. Logical reasoning can be used to prove that a trick works or, in some cases, doesn’t work. It can help find a solution to puzzles or games that are not logic games.
Did You Know?
There have been hundreds of articles and books written about mathematical games. Martin Gardner (1914–2010) is one author who was extremely influential in attracting people to recreational mathematics. His column in Scientific American introduced many people to the idea that mathematics could be fun.
This lesson will help you answer the following inquiry question:
- How can logical reasoning be used to prove conjectures made about games and puzzles?
Assessment
- Lesson 3 Assignment
All assessment items you encounter need to be placed in your course folder.
Save a copy of the Lesson 3 Assignment to your course folder. You will receive more information about how to complete the assignment later in this lesson.
1.1. Launch
Module 2: Logic and Geometry

Hemera/Thinkstock
Launch
Are You Ready? provides a short pre-test to help you assess your mastery of prior skills and knowledge. If you are successful with these questions, you can move on to the Discover section. If you encounter difficulty with these questions, you can move on to the Refresher to review prior skills.
1.2. Are You Ready?
Module 2: Logic and Geometry
1.3. Refresher
Module 2: Logic and Geometry
Refresher
To watch a video that provides a summary of adding and subtracting polynomials, go to the Internet and type the keywords “Math Dude” into a search engine. These keywords should take you to a website from Montgomery County Public Schools.
On the right side of the website, look for the heading “Algebra 1 Unit 6.” Select the video titled “Polynomial Operations.” You will only need to watch the first 4 minutes and 12 seconds of the video.
1.4. Discover
Module 2: Logic and Geometry
Discover
Arithmagons are number puzzles whose central operation is addition. Arithmagons are based on polygons. For example, a triangular arithmagon has 3 sides while a pentagonal arithmagon has 5 sides. There is a circle at each vertex and a box on each side of an arithmagon.
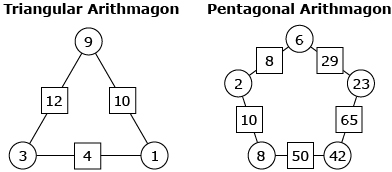
Try This 1
The following Arithmagons applet contains various triangular arithmagons to solve. This activity requires that you apply what you have learned about reasoning to solve arithmagon puzzles.
Follow the instructions in the applet for completing the arithmagons activity.
As you discover the solution to the arithmagons using your own personal strategy, think about any patterns that might be present. For instance, consider what relationship exists (if any) between the
- numbers in the circles and the numbers in the boxes
- number in a circle and the number in the box opposite a circle
Record your conjectures about possible patterns in the arithmagons in your course folder. Once you have completed the applet, you will be sharing your conjectures and thoughts with others in the Share 1 activity. It is important that you keep your responses in a location where they are readily accessible.
Share 1

Marili Forastieri/Digital Vision/Thinkstock
Work with a partner or in a group to discuss your findings from Try This 1.
- Present your conjecture about any patterns you identified about arithmagons in Try This 1 to your group. Describe the pattern you think exists, and give an example of the pattern in an arithmagon. You may choose to present the pattern using words, pictorially, or another method of your choice.
- Once all members of your group have presented their conjectures, compare the patterns. In your discussions, consider the following:
- How are the patterns similar? (Are there any common elements between the patterns?)
- How are the patterns different?
- Do you agree with the patterns presented by other students? (Do the patterns work? Is there a counterexample that disproves the conjecture?) If you don’t agree with other patterns, identify why you think the pattern doesn’t work. (Can you find a counterexample? Can the conjecture be revised to work?)
- How are the patterns similar? (Are there any common elements between the patterns?)
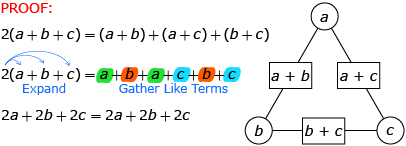
- Based on the patterns you have been presented with, determine a method, strategy, or rule as a group that can be used to describe all arithmagons. The rule may be written out in words, explained using a graphic or algebra, or described using another method of your choosing. For instance, if you are using algebra to describe your solution or pattern, you would have to explain what values are in circles (a, b, and c) and what values are in boxes (d, e, and f) and how they are related.
1.5. Explore
Module 2: Logic and Geometry
Explore
As you completed Try This 1 and Share 1 activities, you may have noticed a few different patterns in the arithmagons. You and your group might have made the following conjectures based on your observations of the patterns in the triangular arithmagons:
- The number in each box is the sum of the two adjacent circle numbers.
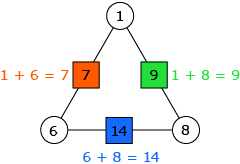
- When the box numbers form a clockwise sequence, the circle numbers form a counter-clockwise sequence.
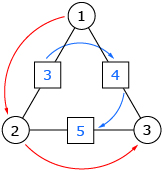
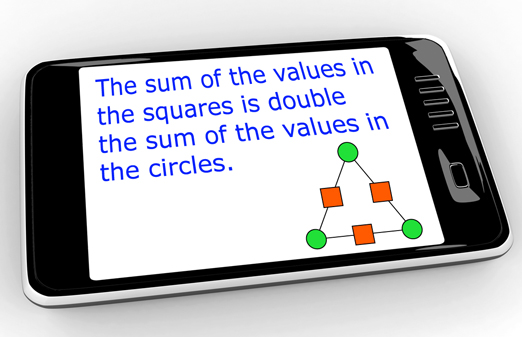
- The sum of the values in the squares is double the sum of the values in the circles.
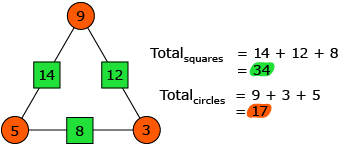
- The sum of the value in a circle and the opposite box is the same number (i.e., the centre number).
The conjectures you made in Discover were based on your observations of patterns in the triangular arithmagons. Inductive reasoning was used to arrive at your conjectures. Recall that conjectures cannot be proven using inductive reasoning. You cannot look at every possible arithmagon, so it is not possible to prove a conjecture using inductive reasoning. When you worked on Share, you and your group may even have revised some of the conjectures if a counterexample was found.
generalization: a statement, principle, or idea that has a general application
The aim of the activity you completed in the Arithmagons applet was to make conjectures about the solutions to triangular arithmagons based on observed patterns and to develop a rule that you can use to solve other triangular arithmagons. In other words, can a rule be written, based on the pattern(s) you identified, and successfully applied to all triangular arithmagons? This rule is known as a generalization.
iStockphoto/Thinkstock
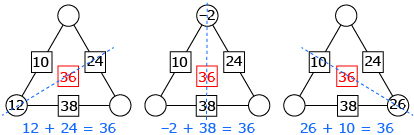
Consider the conjecture Wahid made about triangular arithmagons.
Wahid based his conjecture on evidence he gathered from arithmagons in the Arithmagon applet as well as several other examples.
proof: a logical or mathematical argument that shows a statement is valid in all cases, or that no counterexample exists1
Wahid and his friends Cynthia and Kyle decided they wanted to prove that Wahid’s conjecture was true for all triangular arithmagons. Watch the animation From Conjecture to Generalization to see how Wahid’s group developed its proof.
Wahid and his friends proved that the sum of the values in the squares will always be equal to twice the sum of the values in the circles in all triangular arithmagons. The steps that Wahid, Cynthia, and Kyle used to determine that the generalization is valid in all cases are called a proof.
deductive reasoning: a type of reasoning used to draw a specific conclusion through logical reasoning by starting with statements that are accepted as true (valid)2
The process of generalizing a conjecture is called deductive reasoning. Deductive reasoning uses a well-developed system of logic to prove a conjecture. This kind of reasoning starts with general statements that are assumed to be true and derives specific conclusions. So deductive reasoning goes from the general to the specific. This is the opposite of inductive reasoning, which goes from the specific to the general. Inductive reasoning starts with specific assumptions and concludes something general.
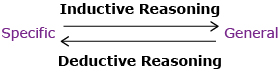
Recall that inductive reasoning can never be used to prove a conjecture. Since it is not possible to observe every known case, reasoning by induction is not logically valid. Inductive reasoning can be involved in the discovery process that produces conjectures, but deductive reasoning is required to prove the conjecture.
1, 2 Adapted from: CANAVAN-MCGRATH ET AL. Principles of Mathematics 11, © 2012 Nelson Education Limited. p. 27. Reproduced by permission.
1.6. Explore 2
Module 2: Logic and Geometry
Self-Check 1
Recall from the Course Introduction that you will be creating your own course glossary. Open the Glossary Terms document now and add any new terms to this document. Alternatively, you may choose to work from the Glossary Terms document you started in Module 1 and continue to add terms to it. Remember to save your document to your course folder.
In Lesson 2 you looked at how inductive reasoning was used to develop a conjecture about perfect squares. Recall that Steffan suggested that the difference between consecutive squares is always an odd number. If you need to review Steffan’s approach, watch Steffan’s Solution animation. You can also read about his method on page 9 of your textbook.
More support was provided for Steffan’s conjecture while Francesca’s conjecture was invalidated by a counterexample in Lesson 2. Even though more evidence was provided, Steffan’s conjecture was never proven to be true for all natural numbers.
To see how deductive reasoning can be used to generalize Steffan’s conjecture, watch the animation Proving Steffan’s Conjecture.
Alternatively, you can read "Apply the Math" on page 28 of your textbook. As you watch the animation or read about the proof, think about how the diagram helped to express the conjecture as a rule or general statement.
Adapted from: CANAVAN-MCGRATH ET AL. Principles of Mathematics 11, © 2012 Nelson Education Limited. p. 28.
Reproduced by permission.
If you feel you need another example of how deductive reasoning is used, read “Learn About the Math” and “Example 1: Connecting conjectures with reasoning” on page 27 of your textbook. As you read, consider the following questions:
- What type of reasoning did Jon use to make his conjecture?
- What type of reasoning did Pat use to prove Jon’s conjecture?
- What is the difference between the two types of reasoning they each used?
1.7. Explore 3
Module 2: Logic and Geometry
Self-Check 2
- Complete “Practising” question 17 on page 24 of your textbook. Answer
- Complete “Practising” question 9 on page 32 of your textbook. Answer
- Complete “Practising” questions 4 and 5 on page 31 of your textbook. Answer
Remember that the purpose of a proof is to show that the conjecture is true in all cases. The specific strategy that is used for a proof will vary based on the conjecture and the individual’s personal strategy for creating the proof. When deductive reasoning is used correctly in a proof, you can be sure that the conclusion you draw is valid.
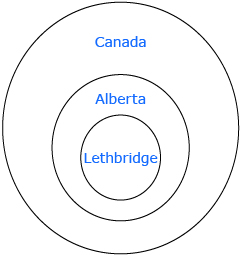
Not all proofs involve or require algebra. Proving a statement using deductive reasoning can be done in a variety of ways. Proofs might involve the organization and visualization of given statements in a Venn diagram to make a valid conclusion. For example, a Venn diagram can be used to prove that all people in Lethbridge live in Canada.
A two-column proof might also be used to prove a conjecture. You will look at more examples of two-column proofs later in this module when you look at possible strategies for proving geometric conjectures.
Venn diagram: a type of diagram used to picture sets and the relationships between them
two-column proof: a presentation of a logical flow of statements in the left-hand column and the reasons or justifications why each of these statements are valid in the right-hand column of a table
— Adapted from: CANAVAN-MCGRATH ET AL. Principles of Mathematics 11,
© 2012 Nelson Education Limited. p. 29. Reproduced by permission.
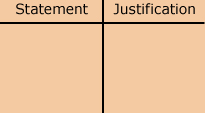
To see an example of a proof using a Venn diagram and an example with a two-column proof, read “Example 3: Using deductive reasoning to make a valid conclusion” and “Example 4: Using deductive reasoning to prove a geometric conjecture” on page 29 of your textbook. As you read the examples, consider how Venn diagrams and two-column proofs help to visualize and organize the statements.
If you haven’t done so already, now would be a good time to update your Glossary Terms document. Remember to save your updated document to your course folder.
Self-Check 3
- Complete “Check Your Understanding” question 2 on page 31 of your textbook. Answer
- Complete “Practising” question 8 on page 32 of your textbook. Answer
In this lesson you learned about the type of reasoning required to prove conjectures. If you haven’t done so already, update your notes organizer with any thoughts or key ideas about inductive and deductive reasoning. For instance, you might find it helpful to add an example of a proof. The “Mid-Chapter Review” on page 34 of your textbook provides some frequently asked questions you can use to get started.
1.9. Lesson 3 Summary
Module 2: Logic and Geometry
Lesson 3 Summary
In Lesson 3 you looked at how logical reasoning can be used to prove conjectures made about games and puzzles. Deductive reasoning uses a well-developed system of logic to prove a conjecture.
You begin by making a conjecture—this is usually based on observation. Inductive reasoning is used to develop a rule or generalization from a conjecture. Remember that inductive reasoning moves from the specific to the general. You then use deductive reasoning to show that the generalization can be applied to all possible cases, which, logically proves conjectures.
For instance, Wahid made a conjecture in this lesson for describing the triangular arithmagons. The conjecture was expressed as a general statement that can be applied to all triangular arithmagons. Wahid’s group then proved that its generalization was valid for all triangular arithmagons, as shown in the following proof.
Remember that deductive reasoning is the opposite of inductive reasoning. Inductive reasoning starts with specific assumptions and concludes something general. Deductive reasoning starts with general statements that are assumed to be true and derives specific conclusions.
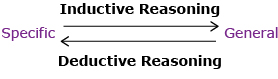
Proofs can take on a variety of forms. They may involve algebra, Venn diagrams, or tables that relate statements and justifications (e.g., two-column proofs). The strategy used to prove a conjecture using deductive reasoning will depend on the conjecture as well as the personal strategy of the person writing the proof.
When deductive reasoning is used correctly, you can be sure that the conclusion you draw is valid. However, proofs arrived at by deductive reasoning can be invalid if the reasoning is flawed. In Lesson 4 you will further investigate deductive reasoning and learn how to identify when the reasoning contains an error.