Lesson 4
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-2 SS |
| Book: | Lesson 4 |
| Printed by: | Guest user |
| Date: | Tuesday, 30 December 2025, 9:46 AM |
Description
Created by IMSreader
1. Lesson 4
Module 2: Logic and Geometry
Lesson 4: Identifying Errors in Proofs
Focus

iStockphoto/Thinkstock
Many types of puzzles or problems involve the use of reasoning to solve a mystery. TV shows like CSI or NCIS often have the lead detectives make a conjecture about the identity of the murderer and then justify their reasoning through investigation.
Not all reasoning used to justify a proof is valid. For instance, circumstantial evidence often points at one suspect and, often times, once the forensic analysis is done, a different suspect is identified.
This lesson will help you answer the following inquiry question:
- How can the validity of a proof be justified?
Assessment
- Lesson 4 Assignment
All assessment items you encounter need to be placed in your course folder.
Save a copy of the Lesson 4 Assignment to your course folder. You will receive more information about how to complete the assignment later in this lesson.
1.1. Discover
Module 2: Logic and Geometry
Discover
In order for a proof to be valid, the arguments used to support the generalization or conclusion must be valid.
Read “Example 5: Communicating reasoning about a divisibility rule” on page 30 of your textbook. As you examine Lee’s proof, consider why his proof is valid based on what you have learned about deductive reasoning in Lesson 3.
Try This 1
Consider the following sets of integers:
| 10, 11, 12 | 5, 6, 7, 8, 9 | 1, 2, 3, 4, 5, 6, 7 |
- Show that the sum of each set of consecutive integers divided by the number of integers in the set is equal to the middle term in each set of numbers. For example,

-
Form a deductive proof that the sum of any set of 5 consecutive integers divided by the number of integers in the set (5) is equal to the middle term in each set.

iStockphoto/Thinkstock
Share 1
Having a discussion with a partner or group will help to identify alternative strategies that may be effective in developing a deductive proof. As well, you may discover a way to revise your personal strategy to make it more efficient.
Compare your answers from Try This 1 with a partner or in a group. In your discussion, discuss the following questions:
- When you divided the sum of each set of numbers by the number of integers in the set in question 1, did you get the middle term of the set?
- What strategy did you each use to write a deductive proof for question 2? What did your proof look like?
- Did the strategies used result in a valid proof? If not, can you identify any errors in the proof?
After completing the preceding activities, Joel decides that he wants to look at an even number of consecutive integers. He decides to prove that the sum of 4 consecutive integers is evenly divisible by the number of integers in the set (4).
You can watch the animation titled Joel’s Solution.
A copy of Joel’s Solution: Print Version is also available. You may find it helpful to have a copy of his solution handy when you work on the Share 2 questions.
Share 2
After examining Joel’s proof, answer the following questions with a partner or group:
- Is Joel’s proof valid? Why or why not? If the proof is incorrect, identify the error.
- How could a counterexample be used in this situation? Provide an example.
1.2. Explore
Module 2: Logic and Geometry
Explore
invalid proof: a proof that contains invalid assumptions or has an error in reasoning1
Earlier in this module, you learned that conjectures based on inductive reasoning may be valid for specific examples but cannot be proven. It is impossible to look at all possible cases. Conjectures can be weakened by insufficient evidence or by ignoring counterexamples (e.g., only testing those cases that you know support the conjecture). Conjectures can also be invalidated by a single counterexample. In a similar way, proofs can be invalidated if there are errors in the proof or if invalid assumptions are used when developing the proof. In Lesson 3 you learned how deductive reasoning can be used to prove conjectures. However, not all proofs are valid. Joel’s Solution is an example of an invalid proof.
Joel’s proof contained an error. In his solution, Joel did not divide both terms in the numerator by the term in the denominator.
Joel’s Solution
Let n represent any integer.
Let n + (n + 1) + (n + 2) + (n + 3) represent a sum of 4 consecutive integers.
So, ![]() represents the sum of the 4 consecutive integers divided by the number of integers in the set (4).
represents the sum of the 4 consecutive integers divided by the number of integers in the set (4).
I can simplify this as shown:

Since 4n can be divided by 4, this proves that the sum of four consecutive integers is evenly divisible by the number of terms.
Dividing both terms in the numerator by the denominator results in n + 1.5.
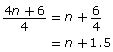
Since 6 is not evenly divisible by 4, this counterexample disproves the conjecture that the sum of an even number of consecutive integers is evenly divisible by the number of integers.
Sometimes the identification of an error in a proof can be used to correct mistakes in a proof.
Read “Example 4: Using reasoning to determine the validity of a proof” on page 40 of your textbook to see a situation where correcting a mistake made the proof valid.
You probably noticed that Joel and Hossai made the same type of error. Each forgot to divide both of the terms in the polynomial by the divisor. However, correcting the error had very different results. It is important to review each step of your proof for errors before you declare whether it is valid or not.
1 Adapted from: CANAVAN-MCGRATH ET AL. Principles of Mathematics 11, © 2012 Nelson Education Limited. p. 37. Reproduced by permission.
1.3. Explore 2
Module 2: Logic and Geometry
Self-Check 1
Complete “Practising” question 5 on page 43 of your textbook. Answer
Identifying errors in a proof may involve understanding the way mathematical operations are allowed to be applied. Logically, you know that 1 does not equal 2; but some proofs can be quite convincing. Watch Proving 2 = 1 and see if you can spot the error in the proof.
Read “Example 2: Using reasoning to determine the validity of a proof” on pages 37 and 38 of your textbook. How is the error in this proof similar to the error in the proof that 2 = 1?
Self-Check 2
Complete “Practising” question 3 on page 42 of the textbook. Answer
premise: a statement assumed to be true1
Proofs that include an argument that is based on a false statement are invalid. Even if a valid argument is used, if one or more of the starting premises are not true, the conclusion cannot be true.
Read “Example 3: Using reasoning to determine the validity of a proof” on page 39 of your textbook. As you read, think about what happens to a conclusion that is based on a false assumption?
circular reasoning: an argument that is incorrect because it makes use of the conclusion to be proved2
Example 3 is an example of circular reasoning. Circular reasoning uses the conclusion that is to be proved as part of the argument. In other words, you assume that what you are supposed to be proving is true and use that statement as part of your proof. This is like arguing in a circle and is not a valid form of reasoning. The following statements and arguments are examples of circular reasoning.

1 Adapted from: CANAVAN-MCGRATH ET AL. Principles of Mathematics 11, © 2012 Nelson Education Limited. p. 38. Reproduced by permission.
2 Adapted from: CANAVAN-MCGRATH ET AL. Principles of Mathematics 11, © 2012 Nelson Education Limited. p. 39. Reproduced by permission.
1.4. Explore 3
Module 2: Logic and Geometry
Errors in logic can also lead to invalid conclusions. Take a look at the following cartoon.

© 1997 Randy Glasbergen. www.glasbergen.com
It is true that penguins are black and white. It is true that some old television shows are black and white. To deduce from those two statements that penguins are old TV shows is not logical. There is no connection between the two statements. When there is an error in logic (an invalid argument), no reliable conclusion can be made regardless of whether the premises are true.
Share 3
Consider the following arguments. A Venn diagram can be used to examine each argument.
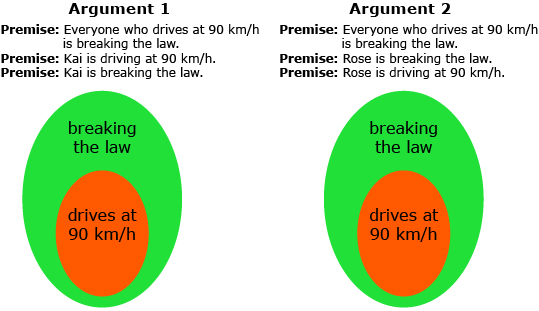
With a partner, discuss whether each argument is valid and justify your reasoning. How do the diagrams help you to answer this question? Where does Kai’s name belong in the Venn diagram? Where does Rose’s name belong in the Venn diagram?
Self-Check 3
- Decide whether this argument is valid or invalid. Justify your response:
- Val lives in Sylvan Lake. All people who live in Sylvan Lake like to swim. Therefore, Val likes to swim. Answer
- A pound of Julia’s Special Blend coffee costs more than $22.75 per pound. John didn’t buy Julia’s Special Blend when he purchased coffee. Therefore, John didn’t spend more than $22.75 per pound. Answer
- Complete “Practising” questions 4 and 6 on pages 42 and 43 of your textbook. If you don’t have a house number (street address number), make one up for question 6. Answer
If you haven’t done so already, organize your thoughts on identifying errors in proofs in your notes organizer. You might find it helpful to identify specific types of errors that invalidate a proof, such as mathematical errors like dividing by zero or errors in logic like circular reasoning. Reading “In Summary” on page 41 of your textbook may be useful for helping to organize the key ideas of this lesson.
1.6. Lesson 4 Summary
Module 2: Logic and Geometry

Sidney Harris/ScienceCatoonsPlus.com
Lesson 4 Summary
In this lesson you discovered that not all proofs are valid. A proof can be invalidated by a single error in reasoning. That error may be the result of division by zero somewhere in the proof. The use of circular reasoning or another type of error in logic also results in an invalid proof. For instance, when reasoning relies on stereotypes, the conclusions are not valid. Stereotypes are generalizations and there are always counterexamples to stereotypes.
An error in a proof is similar to a counterexample in that it only takes one error to invalidate the conclusion. For example, a proof that is based on a false premise is invalid, even if the argument used is valid.
In Lesson 5 you will apply what you have learned about reasoning to solve problems.