Lesson 5
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-2 SS |
| Book: | Lesson 5 |
| Printed by: | Guest user |
| Date: | Tuesday, 30 December 2025, 9:48 AM |
Description
Created by IMSreader
1. Lesson 5
Module 2: Logic and Geometry
Lesson 5: Reasoning to Solve Problems, Puzzles, and Games
Focus
Inductive reasoning and deductive reasoning can be used to solve problems, analyze puzzles, and win games. Reasoning is required to solve a logic puzzle, win a board game, or outsmart your opponents in a video game. You might not even realize it, but when you are playing these games or trying to figure out a puzzle, you are using reasoning to solve problems. You’re giving your brain a workout.
Did You Know?
Patolli, which is similar to modern-day backgammon, and bul are two board games played by ancient Mesoamericans. They were used for recreation as well as for religious purposes. These games blend strategy and chance. Want to know more about these ancient board games? An Internet search for patolli and bul will suggest websites. You might even find a
computer-based version of the games!
You have already looked at some examples in previous lessons where inductive and deductive reasoning were used to solve problems, solve a puzzle, or determine a strategy for a game. In this lesson you will learn to identify the type of reasoning used in the solution. Was inductive reasoning used? Was deductive reasoning used? Were both types of reasoning used in the solution? You will also learn to recognize features of problem-solving strategies that use each type of reasoning.
This lesson will help you answer the following inquiry questions:
- How can inductive and deductive reasoning be used in problem solving?
- How can inductive and deductive reasoning be used to determine a strategy to solve a puzzle or win a game?
Assessment
- Try This 2
- Share 1
- Lesson 5 Assignment
All assessment items you encounter need to be placed in your course folder.
Save a copy of the Lesson 5 Assignment to your course folder. You will receive more information about how to complete the assignment later in this lesson.
1.2. Discover
Module 2: Logic and Geometry

Hemera/Thinkstock
Discover
Inductive reasoning and deductive reasoning are helpful in problem solving. You have looked at examples of inductive and deductive reasoning in previous lessons in this module. In Lesson 3 you used inductive reasoning to identify patterns in triangular arithmagons. Deductive reasoning was then used to prove a general rule for triangular arithmagons. In each of these instances, you used your own personal strategy to solve the given problem.
Read “Investigate the Math” on page 45 of your textbook. As you read, think about the strategy Emma used to develop her conjecture and then to prove her conjecture.
A clear explanation of the steps used to solve a problem ensures that whoever is reading the explanation can follow the reasoning all the way through. For instance, Emma used a chart to organize the examples she used to develop her conjecture. Her evidence included a variety of values—positive and negative, large and small—which strengthened her conjecture. This structured approach allows other people to work through the evidence provided and generally follow her reasoning. However, Emma’s communication about her reasoning can be improved.
Try This 1
Using what you know about inductive and deductive reasoning, identify how Emma’s communication about her reasoning could be improved.
- Complete “Investigate the Math” questions A, B, and C on page 45 of your textbook. Note that question A asks that you work with a partner, if you can.
- Complete “Reflecting” questions D and E on page 46 of your textbook.
- Use what you have learned about inductive and deductive reasoning in this module to create a set of steps that can be used to form a conjecture; then prove or disprove it.
Did you or your partner you worked with in question A notice that Emma’s proof did not include reasons for each step? She only provided a summary. In order for other people to fully understand her proof, she needed to include more details of her deductive reasoning process. These details should include justifications and explanations of her reasoning, shown in the following example.

If steps are missing, the reader may not understand the reasoning or may reject the argument as invalid. Likewise, the wording, diagrams, or algebra used must be clear so that the reader understands the reasoning behind the solution. Regardless of whether inductive reasoning, deductive reasoning, or both types of reasoning are used to solve a problem, the strategy used must be clear.
1.3. Explore
Module 2: Logic and Geometry
Explore
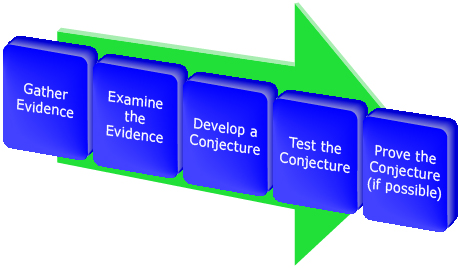
You may have noticed as you worked through this module that inductive and deductive reasoning processes each involve a series of steps. For instance, the following steps can be used to form a conjecture and then used to prove or disprove it. Watch the animation called Steps.
Self-Check 1
- Which step or steps in the Steps animation involve inductive reasoning? Answer
- Which step or steps apply to deductive reasoning? Answer

Hemera/Thinkstock
Read “Example 1: Using reasoning to solve a problem” and “Example 2: Using reasoning to solve a problem” on pages 46 to 48 of your textbook. As you read, think about the following questions:
- What strategy was used to solve each problem?
- Was inductive or deductive thinking used in the solutions for Example 1 and Example 2?
- How do you know which type of reasoning was used?
- Did the problem-solving strategy give you any clues as to which type of reasoning was used?
As you have seen throughout this module, inductive reasoning involves observing patterns. A logical conclusion is then drawn based on these observations to solve the problem. For example, inductive reasoning was used to determine how many handshakes were exchanged by examining the pattern in the first two cases.
Deductive reasoning uses known facts or assumptions to develop an argument. This argument is then used to draw a logical conclusion and solve the problem. Vicky used deductive reasoning to determine the four pairs of partners for fun night.
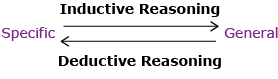
Self-Check 2
1.4. Explore 2
Module 2: Logic and Geometry
Try This 2
Submit your work for Try This 2 to your teacher for marking.
Complete “Practising” question 10 on page 50 of your textbook. (This question is assigned 5 marks. You will be marked out of a possible 3 marks for 10.a. and 2 marks for 10.b.)
Share 1
Submit your work to Share to your teacher for marking.
Complete question 12 of “Practising” on page 50 of your textbook. Note that you are required to work with a partner to complete question 12.b. (This question is graded out of 4 marks. You will be graded out of a possible 2 marks for 12.a. and 2 marks for 12.b.)
Lesson Assignment
1.5. Explore 3
Module 2: Logic and Geometry
Winning a game or solving a puzzle requires a problem-solving approach. In earlier lessons, you identified patterns in games and puzzles and then developed a strategy to fit the pattern. The strategy may even have been developed using steps similar to the ones you identified for using reasoning to solve problems. Strategies can be adapted to come up with the best possible strategy for winning a game. The same approach of adapting strategies can be applied whether you are trying to solve a puzzle or figuring out how to maximize seating in a cafeteria.
Read “Example 1: Using reasoning to determine possible winning plays” on page 53 of your textbook. As you read, think about the strategies each player might use to win the game. What other way could Frank win the game on his turn? What strategy could Tara use to win on her next turn, if Frank does not win on his turn?

iStockphoto/Thinkstock
Analyzing possible strategies using inductive and deductive reasoning can be helpful in winning a game. By determining what your moves need to be based on your opponent’s possible strategy, you can stay one move ahead of your opponent. In other words, you use reasoning to look ahead and try to figure out what your opponent might do next.
For instance, in the game tic-tac-toe, there are only a few moves for the entire game. You can deduce your next move from your opponent’s previous move and your knowledge of the point of the game. Part of your strategy is trying to figure out how to get three X’s in a row. The other part is trying to figure out how to stop your opponent from getting three O’s in a row. This requires looking ahead and adapting your strategy based on where you and your opponent could place your X’s and O’s.
Did You Know?
Noughts and crosses or three-in-a-row are other names for tic-tac-toe. These games may have been played as far back as 1300 BCE in Egypt. Grid games such as tic-tac-toe have been recorded in carvings from ancient Roman times.
—Adapted from: CANAVAN-MCGRATH ET AL. Principles of Mathematics 11 TR, © 2012 Nelson Education Limited. p. 39. Reproduced by permission.
In chess, players may use inductive reasoning to determine their strategy. A player may study the current placement of pieces on the board while thinking about the opponent’s play in previous games. Evidence is used to identify patterns. Based on these patterns, a player can make conjectures about his or her opponents’ intended moves and strategy.
![]()
“If . . . then” statements can be used to help determine an appropriate strategy. For instance, you might ask yourself, “If I do this, then what move could my opponent make?” You can do this for any number of possible scenarios. “If I do this instead, then what move could my opponent make?”
Read “Example 2: Using deductive and inductive reasoning to determine a winning strategy” on page 54 of your textbook. In this example, both inductive and deductive reasoning are involved in the strategy.
1.6. Explore 4
Module 2: Logic and Geometry
Self-Check 3
Complete “Your Turn” on page 54 of your textbook. Answer
Example 1 and Example 2 of your textbook show that both inductive and deductive reasoning are useful for developing winning strategies. Inductive reasoning is useful for solving puzzles or winning games that require recognizing patterns, extending a pattern, or identifying a certain order. For games and puzzles that require inquiry and discovery to complete, deductive reasoning is a useful strategy.
Review the “In Summary” boxes on pages 48 and 55 of your textbook. As you read, consider how inductive and deductive reasoning can help you to solve problems, strategize to win a game, or solve a puzzle.
You might choose to include the information in the “Key Idea” and “Need to Know” sections in your notes organizer.
Self-Check 4
1.8. Lesson 5 Summary
Module 2: Logic and Geometry
Lesson 5 Summary
Throughout this module, you have explored personal strategies used to solve problems. There are steps that can be used to identify patterns, determine and adapt strategies, and solve the problem. The solutions to problems, puzzles, or games can involve inductive reasoning, deductive reasoning, or both types of reasoning. Whether inductive or deductive reasoning is used, it is important that the solution have enough information so that other people can read and understand the solution.
In this lesson you have seen examples where inductive reasoning was used as part of the solution. These examples involved solving puzzles or winning games that required recognizing patterns, extending a pattern, or identifying a certain order. Games and puzzles were also presented that used deductive reasoning as part of the winning strategy. These games and puzzles were types that required inquiry and discovery to complete. Some problems required both types of reasoning.
In this lesson you applied what you learned about making and proving conjectures to solving problems. For the remainder of this module, you will apply what you have learned about inductive and deductive reasoning to solve geometric problems that involve the properties of angles and triangles.
