Lesson 6
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-2 SS |
| Book: | Lesson 6 |
| Printed by: | Guest user |
| Date: | Tuesday, 30 December 2025, 9:49 AM |
Description
Created by IMSreader
1. Lesson 6
Module 2: Logic and Geometry
Lesson 6: Exploring Parallel Lines
Focus

In earlier lessons you looked at various examples of patterns in games and puzzles. You analyzed specific patterns of moves in an actual game or patterns in the puzzle to develop winning strategies. Inductive reasoning is not only helpful in determining patterns in game play; it can also be used to identify geometric relationships in the design of the game or puzzle.
Consider the game fox and geese. It is played on a cross-shaped board with 33 holes. The holes are connected by straight and diagonal lines. This game dates back to the Middle Ages in Europe. There are many versions of this game. For instance, some First Peoples have a game that, when translated, is called “playing leader.” In Japan, the game is known as juroku musashi or “sixteen soldiers.”
The design of the game surface is crucial to how the game is played. The position of the holes and the arrangement of the lines determine how the fox and the geese can move. Many factors go into successful design. Relationships between elements in the design, such as angles and lines, are carefully examined. This information is vital to ensure that the design can be recreated.
This lesson will help you answer the following inquiry questions:
- What relationships can be identified between pairs of angles formed by transversals and parallel lines in various designs?
- How can inductive reasoning be used to make conjectures about the relationships of angles formed when a line intersects a pair of parallel lines?
Assessment
- Try This 4
- Lesson 6 Assignment
All assessment items you encounter need to be placed in your course folder.
Save a copy of the Lesson 6 Assignment to your course folder. You will receive more information about how to complete the assignment later in this lesson.
You will be presented with a number of definitions in this lesson. Remember to add any definitions and corresponding diagrams to your Glossary Terms document.
Materials and Equipment
1.2. Discover
Module 2: Logic and Geometry
Discover

The design of an actual board game or screen background is an important part of creating a successful game. Ensuring that each version of the game is the same is also extremely important. This is particularly true in the game fox and geese where the lines indicate movement of the pieces.
Regardless of whether the playing pieces are known as geese, fox, soldiers, or pegs, the movement of the pieces is similar. To win, the geese have to surround the fox so he cannot move or jump. At least six geese are required to surround the fox. For the fox to win, the geese must all be captured or the fox must make it to the bottom of the board.
The fox captures a goose by jumping over a goose into the empty spot next to it. The fox can move left, right, up, or down. The geese may move right, left, or down. The geese can use the diagonals to move, but they cannot go backwards. The geese also cannot jump like the fox can. Some variations of the game prevent the fox from moving diagonally.
The game fox and geese can be used to investigate the relationships between pairs of angles formed between lines. There are several intersecting lines on the game board. The diagonal lines intersect with the horizontal and vertical lines. The horizontal and vertical lines intersect with each other.
1.3. Discover 2
Module 2: Logic and Geometry
Try This 1
Use the applet Opposite Angles to determine the relationship between the angles formed by two intersecting lines. From your observations, what conjecture can you make about opposite angles? ![]() Move the position of the intersecting lines by clicking on the blue points on any of the lines. Does your conjecture still hold when you reposition the lines?
Move the position of the intersecting lines by clicking on the blue points on any of the lines. Does your conjecture still hold when you reposition the lines?
In Try This 1, you made a conjecture about opposite angles based on your observations. In Try This 2 you will expand on this by considering what relationships exist between angles when another line is added.
Try This 2
Use the animation Angles and Lines to investigate what relationships exist between the eight angles that are formed when two or more lines intersect. As you compare the measures of the angles, see what happens to the angles when you move various lines. For instance:
- What happens to the measure of the angles when you move line QR?
- What happens to the measure of the angles when you move line ST?
- What happens to the measure of the angles when you move line UV?
- Does it matter whether the lines are parallel or non-parallel?
Try This 2 activity allowed you to examine angles formed when a line intersects two parallel or two non-parallel lines. When any two lines are intersected by a third straight line, we call that line a transversal. When a transversal intersects a pair of lines, two sets of angles are created.
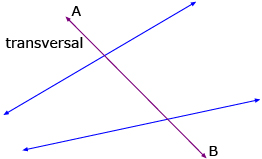
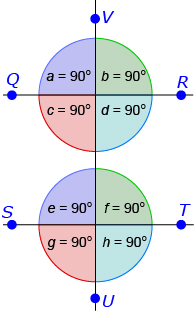
When the parallel lines QR and ST are intersected by the transversal UV, a total of eight angles are formed. UV intersecting QR creates angles a, b, c, and d. UV intersecting ST creates angles e, g, f, and h.
In Try This 3, you will focus on parallel lines intersected by a transversal. You will consider the relationships between all eight angles formed by this intersection.
1.4. Discover 3
Module 2: Logic and Geometry
Try This 3
Use the applet Parallel Lines to compare the relationships between angles formed when two parallel lines are intersected by a transversal.
- Move the location where line UV (the transversal) crosses the two parallel lines by moving point U or point V. How are the angles related when a transversal intersects two parallel lines? (Be sure to also consider relationships between all eight angles).
- Click on point Q to move the direction of the parallel lines QR and ST.
- What do you notice about the relationships between the measures of the angles when the direction of the parallel lines changes? Based on your observations, make at least three conjectures about the relationships between angles formed when two parallel lines are intersected by a transversal. You may choose to describe your conjectures using words, a diagram, or the strategy of your choice.
Share 1
Compare your observations and conjectures you developed from using the applets in Try This 1, Try This 2, and Try This 3 with another student or appropriate partner. In your discussion, consider the following questions:
- How are your conjectures about relationships between angle measures similar? How are they different?
- What do your findings from Try This 2 tell you about your conjectures for angles formed in Try This 3 for when a line intersects two parallel lines? For instance, do your conjectures apply to non-parallel lines as well?
- Based on your conversations, do you feel you need to revise any of your conjectures from Try This 1 and Try This 3?
1.5. Explore
Module 2: Logic and Geometry
Explore

iStockphoto/Thinkstock
Inductive reasoning has been used in this lesson to develop conjectures about the relationships between angles and intersecting lines. As you have seen in previous lessons, inductive reasoning begins with specific assumptions and concludes with something general. These conclusions may or may not be true for all cases. In fact, you should recall that only one counterexample is enough to make the conjecture invalid.
In the Try This activities, you made conjectures about the relationships between pairs of angles formed by intersecting lines using inductive reasoning. For instance, in Try This 1 you may have made the conjecture that opposite angles are congruent or equal in measure. You can go back to Try This 1 and use the Opposite Angles applet to review your conjecture.
In Try This 2 and Try This 3, you observed relationships between angles formed when a transversal intersects two lines. Rozanna and Josh also made conjectures based on the relationships they observed between the measures of the interior angles and exterior angles in Try This 2 and Try This 3.
interior angles: angles that are located between two lines intersected by a transversal
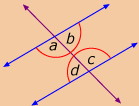
exterior angles: angles that are located outside two lines intersected by a transversal
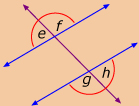
Based on her observations, Rozanna made the following conjecture: When a transversal intersects two parallel lines, the corresponding angles are always equal.
corresponding angles: angles that are in the same position relative to lines intersected by a transversal
One way to find corresponding angles is to draw the letter F on the diagram. This can be forwards, backwards, and even upside down.

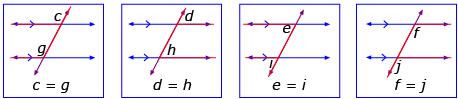
Rozanna supported her conjecture with the following diagrams.
converse: a statement that is formed by switching the premise and the conclusion of another statement1
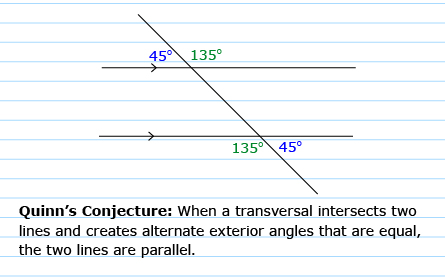
Josh said that the converse of Rozanna’s conjecture was also true. He concluded that when a transversal intersects two lines and creates corresponding angles that are equal, the two lines are parallel. Josh’s conjecture switches Rozanna’s premise about equal corresponding angles with her conclusion that the lines are parallel.

1 Adapted from: CANAVAN-MCGRATH ET AL. Principles of Mathematics 11, © 2012 Nelson Education Limited. p. 71. Reproduced by permission.
You may want to verify Rozanna’s and Josh’s conjectures using the Angles and Lines animation. (You first used this multimedia item in Try This 2.) Can you find any counterexamples for their conjectures? Also, consider whether Rozanna’s and Josh’s conjectures can be expanded to include non-parallel lines. In other words, are corresponding angles equal when a transversal intersects a pair of non-parallel lines?
1.6. Explore 2
Module 2: Logic and Geometry
Self-Check 1
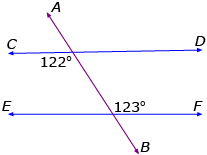
In each diagram, is CD parallel to EF? Explain how you know.
a. 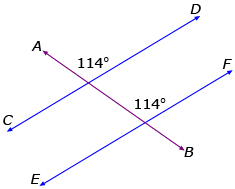
Answer
b. 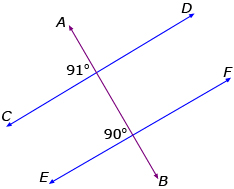
Answer
Sue also observed some relationships between pairs of angles formed by transversals and parallel lines. Based on her observations from Try This 2 and Try This 3, Sue concluded that the interior angles on the same side of a transversal that intersects a pair of parallel lines are supplementary. (Supplementary angles add up to 180°.) These are sometimes referred to as consecutive interior angles because they are next to one another. A quick way to find these angles is to draw the letter C on the diagram (either backwards or forwards).
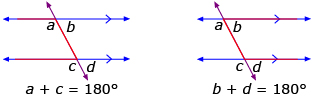
Self-Check 2
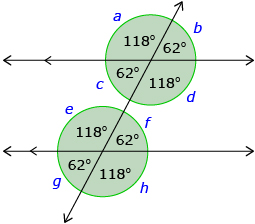
There are a number of pairs of supplementary angles in addition to consecutive interior angles.
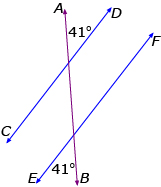
Identify the supplementary angles in the following diagram. Answer
Instead of using the Angles and Lines applet and the Parallel Lines applet to gather evidence, Quinn decided to use a protractor to measure the angles formed by the intersecting lines on the fox and geese game board. Quinn focused on the relationship between alternate angles on the game board. Specifically, he considered the alternate exterior angles.
alternate angles: two non-adjacent angles on opposite sides of a transversal
There are alternate interior angles and alternate exterior angles. Alternate angles form a Z shape.
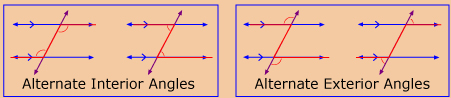
alternate exterior angles: two exterior angles formed between two lines and a transversal, on opposite sides of the transversal
Watch the animation Angles of Play to see the evidence Quinn collected and the conjecture he developed based on his evidence.
1.7. Explore 3
Module 2: Logic and Geometry
Try This 4
You will submit your answers from Try This 4 to your teacher for marks.
Discuss the method Quinn used to develop his conjecture. In your discussion, consider the following questions:
- How could Quinn strengthen his conjecture? (1 mark)
- Do you have any evidence from your observations of the Angles and Lines applet and the Parallel Lines applet that would strengthen or invalidate Quinn’s conjecture? (1 mark)
- Could a similar conjecture be written for alternate interior angles? What evidence do you have to support this conjecture? (2 marks)
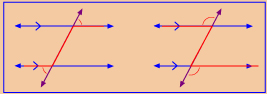
alternate interior angles: two interior angles formed between two lines and a transversal, on opposite sides of the transversal
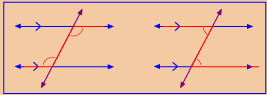
Self-Check 3
- Complete “Further Your Understanding” questions 2, 4, and 5 on page 72 of your textbook. Answer
Inductive reasoning was used to develop several conjectures about the relationships between the angles formed when a transversal intersects a pair of parallel lines. The applet Angle Relationships is a review of the different angle relationships presented in this lesson and will help you to visualize the conjectures that were developed. You will notice that pairs of angles are shown in the same colour. Make sure you only have one angle relationship selected at a time.
If you haven’t done so already, now would be a good time to organize your thoughts and summarize any key ideas from this lesson in your notes organizer.
1.9. Lesson 6 Summary
Module 2: Logic and Geometry
Lesson 6 Summary
The game fox and geese requires the movement of pieces along horizontal, vertical, and diagonal lines on a game board. The design of this game board is an important factor in how the game is played. The characteristics of the game were used in this lesson to investigate relationships between pairs of angles formed between intersecting lines. Based on evidence gathered in various applets, you developed conjectures about these angles and intersecting lines.
Some of the conjectures examined in this lesson can be summarized as follows.
When a transversal intersects two parallel lines, the following are true:
- The corresponding angles are equal (a = e, b = f, c = g, d = h). You can draw the letter F on the diagram to find corresponding angles.
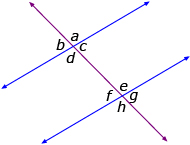
- The alternate interior angles are equal (c = f, d = e). You can draw the letter Z on the diagram; these angles are inside of the Z.
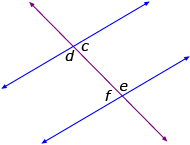
- The alternate exterior angles are equal (a = h, b = g). You can draw the letter Z on the diagram, and these angles are outside of the Z.
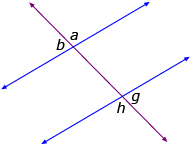
- The interior angles on the same side of the transversal (or consecutive interior angles) are supplementary (c + e = 180°, d + f = 180°). Draw the letter C on the diagram.
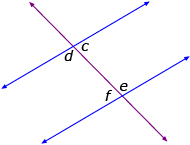
The converse of these conjectures was also supported by the evidence. In other words, if the angles are equal, the lines are parallel. The converse of the conjectures that were just presented is stated in the following way: When a transversal intersects two lines and creates
- corresponding angles that are equal, the two lines are parallel
- alternate interior angles that are equal, the two lines are parallel
- alternate exterior angles that are equal, the two lines are parallel
- interior angles on the same side of the transversal that are supplementary, the two lines are parallel
The evidence also showed that these relationships are only true for parallel lines and their transversals. These conjectures are not true for transversals that intersect two non-parallel lines.
Inductive reasoning was used in this lesson to develop the conjectures that are only true for parallel lines and their transversals. In Lesson 7 you will use deductive reasoning to attempt to prove these conjectures. Any proven conjectures would be known as angle-relationship properties. You will then use these properties to solve problems.