Lesson 7
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-2 SS |
| Book: | Lesson 7 |
| Printed by: | Guest user |
| Date: | Tuesday, 30 December 2025, 9:45 AM |
Description
Created by IMSreader
1. Lesson 7
Module 2: Logic and Geometry
Lesson 7: Proving Conjectures About Angles Formed by Parallel Lines

Hemera/Thinkstock
Focus
Understanding the properties of angles formed by parallel lines and a transversal is important in architecture, engineering, and design. Architects, engineers, and designers use the properties of angles when they are planning projects and evaluating designs. They have to determine what properties are provable and apply those to their designs.

iStockphoto/Thinkstock
The success of a design, not to mention the professional reputation of an engineer or an architect, is based on the expert’s understanding of the properties and his or her ability to apply them correctly. For instance, no one wants to cross a bridge or stand under the roof of a building that someone thinks “might hold” or that has supports that are “hopefully” are at the right angles.
This lesson will help you answer the following inquiry question:
- How can you prove the properties of angles formed by parallel lines and a transversal?
Assessment
- Try This 1
- Lesson 7 Assignment
All assessment items you encounter need to be placed in your course folder.
Save a copy of the Lesson 7 Assignment to your course folder. You will receive more information about how to complete the assignment later in this lesson.
Materials and Equipment
1.1. Launch
Module 2: Logic and Geometry
Launch
Are You Ready?
Help the monkey get to the grocery store by correctly identifying angle relationships in Exploring Parallel Lines (Object Interactive). Click on the “Use It” tab at the bottom of the applet to access the game. This applet will help you determine how comfortable you are with working with the various angle relationships you identified in Lesson 6.
Refresher
Use the “Exploring Parallel Lines (Object Interactive)” applet to review the various angle relationships identified in Lesson 6. Click on the “Explore It” tab to access the applet. Follow the directions in the applet to review the relationships between angles formed when a transversal intersects two parallel lines (“Explore It 1” tab) and two non-parallel lines (“Explore It 2” tab).
1.2. Explore
Module 2: Logic and Geometry
Explore
Did You Know?

Hemera/Thinkstock
Archaeological evidence shows that ancient Americans applied their knowledge of the principles of geometry to architecture and city planning. These principles are also seen in the ornamental designs that were used in sculpture, painting, and textile patterns, such as those woven by the Maya for hundreds of years.
— Emory Dean Keoke, Kay Marie Porterfield. Encyclopedia of American Indian Contributions to the World.
(Facts on File, 2001.) p. 118.
There are many situations where it is important that lines are parallel. The success of designs ranging from railings on stairs to geometric designs on pottery to rehabilitation equipment is dependent on angle properties. Thus, it is crucial that the angle properties being used in the design are proven to be true.

Photodisc/Thinkstock
theorem: a statement that has been accepted as true
Recall from earlier in this module that a proof involves deductive reasoning. In a proof, a specific conclusion is drawn through logical reasoning by using general assumptions that are known to be valid. These assumptions or statements that are accepted as true and used to prove a particular statement or conjecture are sometimes called theorems or properties.
A variety of strategies can be used to prove a conjecture. Sketching a figure that illustrates the situation you are trying to prove is a useful starting point. The diagram can then help you to develop a plan and identify the specific relationships or assumptions you need to include in your proof. You may find that working backwards can help you to identify the relationships and their corresponding statements. Ask yourself questions like, “If the statement I want to prove is valid, what else would have to be valid in my diagram?”

Adapted from: CANAVAN-MCGRATH ET AL. Principles of Mathematics 11 TR, © 2012 Nelson Education
Limited. p. 82. Reproduced by permission.
Organizing the statements in two columns is one way of presenting the proof. This approach is known as a two-column proof. In Lesson 3 you learned that the left-hand column of a two-column proof contains the statements presented in a logical order. The right-hand column of the table has the reasons for or justifications of why each of the statements is valid.
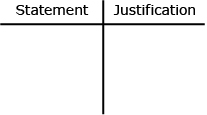
Consider the following situation. Gilles decides to use a two-column proof to prove that the vertically opposite angles are equal in the supporting poles of a trapper’s tent that is set up at a local gathering.
Watch the animation Gilles’s Proof to see how Gilles uses deductive reasoning to prove that vertically opposite angles are equal.

Alberta Economic Development
transitive property: if two quantities are equal to the same quantity, then they are equal to each other
If a = b and b = c, then a = c.
— CANAVAN-MCGRATH ET AL. Principles of Mathematics 11,
© 2012 Nelson Education Limited. p. 29.
Reproduced by permission.
In his proof, Gilles used a diagram to visualize the situation. He used the diagram to reason through the proof. Then he recorded the statements and their justifications in the table. One of his statements in his table was justified by the transitive property. The transitive property says that if two quantities are equal to the same quantity, then they are equal to each other.
Prove ∠d = ∠b.
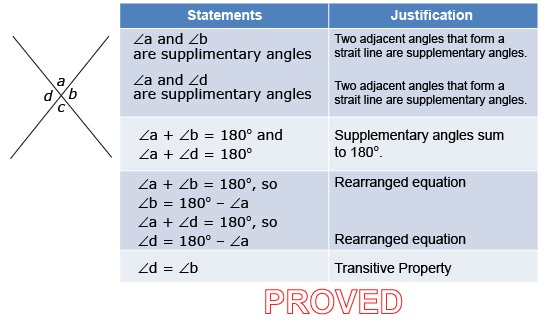
Remember that the purpose of a proof is to show that the conjecture is true in all cases. The specific strategy that is used for a proof will vary based on the conjecture and the individual’s personal strategy for creating the proof.
Read “Example 1: Reasoning about conjectures involving angles formed by transversals” on pages 75 and 76 of your textbook. In this example, two different personal strategies are used to prove two conjectures.
- In the first, Tuyet proves that alternate interior angles are equal when a transversal intersects a pair of parallel lines.
- In the second, Ali proves that interior angles on the same side of the transversal are supplementary when a transversal intersects a pair of parallel lines.
As you read through the two different proofs, consider the similarities and differences in each person’s proof. For instance, in the first solution, Tuyet uses a two-column proof. In the second solution, Ali writes out an explanation of what she did at each step of the proof to demonstrate her reasoning.
1.3. Explore 2
Module 2: Logic and Geometry
Self-Check 1
Complete “Check Your Understanding” question 2 on page 78 of the textbook. Answer
Self-Check 2
Use the following applet titled Self-Check 2 to prove that alternate exterior angles are equal.

Comstock/Thinkstock
When deductive reasoning is used correctly in a proof, you can be sure that the conclusion drawn is valid. If any error occurs, the proof is invalid. Given that many designs are based on the application of angle properties, it is crucial to the success of the designs that errors do not exist in the reasoning behind the designs.
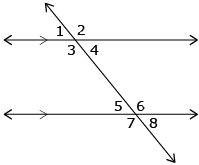
For instance, the design for a cellphone tower is shown in “Example 3: Using angle properties to prove that lines are parallel” on page 77 of your textbook. The design requires parallel braces for the tower. In this example, Morteza and Jennifer used different pairs of angles to prove that the braces on the cellphone tower are parallel.
Read over each proof in Example 3 on page 77 of your textbook. As you examine the proofs, consider what properties of angles each girl used for their proof. A summary of the angle properties related to the angles formed when a transversal intersects two parallel lines is provided.
The lines are parallel if a transversal intersects two lines and the following occurs:
- The corresponding angles are equal: ∠1 = ∠5, ∠2 = ∠6, ∠3 = ∠7, and ∠4 = ∠8.
- The alternate exterior angles are equal: ∠1 = ∠8, and ∠2 = ∠7.
- The alternate interior angles are equal: ∠3 = ∠6, and ∠4 = ∠5.
- The interior angles on the same side of the transversal are supplementary: ∠3 + ∠5 = 180°, and ∠4 + ∠6 = 180°.
1.4. Explore 3
Module 2: Logic and Geometry
Try This 1
You will submit your answer from Try This 1 to your teacher for grading.
Go to the Lesson 7 Assignment that you saved to your course folder. Complete Try This 1. Remember to save your updated Lesson 7 Assignment to your course folder.
Share 1
Present your proof from Try This 1 to another student or appropriate partner. Can you find any errors in each other’s proofs? If so, this makes the proofs invalid. Carefully identify those errors in reasoning. Can these errors be corrected to make the proofs valid? If so, make any necessary corrections in the proof.
The cellphone tower example shows that there may be multiple approaches for creating a valid proof. Each person used the angle properties in a certain way to prove that the braces on the cellphone tower were, in fact, parallel. It also shows the importance of having proofs that are free of errors. If any error occurs, the proof is invalid. Any errors in reasoning could have severe consequences. The cellphone tower braces would not be parallel and would not be constructed properly.
Creating a proof is much like solving a crime. A person needs to survey the crime scene, gather the facts, and then show step by step who committed the crime. It is important to include as much supporting evidence as possible so the judge and jury will be convinced that the crime has been solved. If there is an error in reasoning, an innocent person may be convicted or a guilty person may go free.
Consider the following example.
Amos was asked to prove if line MN was parallel to line OP.
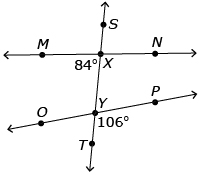
He completed the following proof:
|
Statement |
Justification |
|
∠MXY = 84° |
Given |
|
∠MXY = ∠SXN |
Vertically opposite angles are equal |
|
∠SXN = 84° |
Transitive property |
|
∠NXY = 180° − ∠SXN
∠NXY = 180° − 84°
∠NXY = 106° |
Straight angles = 180° |
|
|
Corresponding angles are equal: ∠NXY = ∠PYT |
Amos has proven that MN is parallel to OP.
Before he hands in his assignment, he asks Miranda to check it over. She tells him that his proof is invalid. Where did he make a mistake? Can you find it?
Amos made a subtraction error in step 4: 108° − 84° = 96°
This means that ∠NXY ≠ ∠PYT, so MN is not parallel to OP.
Remember to always check over your proof for any errors.
Self-Check 3
- Complete “Practising” questions 7, 8, 16, and 19 on pages 79 to 82 of your textbook. Answer
If you feel you need more practice with proofs, complete the following questions.
- “Check Your Understanding” question 1 on page 78 of your textbook Answer
- “Practising” questions 3 and 10 on pages 79 and 80 of your textbook Answer
Read the “Mid-Chapter Review” on page 84 of your textbook. You may want to add some of the points presented on this page to your notes organizer.
1.6. Lesson 7 Summary
Module 2: Logic and Geometry
Lesson 7 Summary
Correctly applying the properties of angles formed by parallel lines and a transversal is important in many aspects of design. Architects, engineers, and designers use the properties of angles to plan their projects. They have to determine what properties are provable and then apply those to their designs.
In a proof, a specific conclusion is drawn through logical reasoning by starting with general assumptions that are known to be valid. This is known as deductive reasoning. These assumptions or statements that are accepted as true and used to prove a particular statement or conjecture are sometimes called theorems or properties.
The purpose of a proof is to show that the conjecture is true in all cases. The specific strategy that is used for a proof will vary based on the conjecture and the individual’s personal strategy for creating the proof. In this lesson you saw a variety of strategies that can be used to prove a conjecture about the angles formed when a transversal intersects a pair of parallel lines.
A useful first step is to make a sketch that illustrates the situation you are trying to prove. The sketch can help you develop a plan and identify the specific relationships or assumptions you need to include in your proof. Working backwards can help identify the relationships and their corresponding statements. Asking yourself questions such as “If the statement I want to prove is valid, what else would have to be valid in my diagram?” can help you to determine which relationships exist.

When deductive reasoning is used correctly in a proof, the conclusion drawn is valid. If any error occurs, the proof is invalid. Architects, engineers, and designers need to ensure that the reasoning behind their designs is not flawed. The success of the project and the reputation of the professional are both dependent on the proofs being valid.
In Lesson 8 you will use what you have learned about deductive reasoning to prove the properties of angles in a triangle.