Lesson 8
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-2 SS |
| Book: | Lesson 8 |
| Printed by: | Guest user |
| Date: | Tuesday, 30 December 2025, 9:21 AM |
Description
Created by IMSreader
1. Lesson 8
Module 2: Logic and Geometry
Lesson 8: Using the Properties of Angles Formed by Parallel Lines to Solve Problems
Focus

iStockphoto/Thinkstock
Did You Know?
The geoglyphs of Nazca were scratched on the surface of the ground between 500 BCE and CE 500. They cover an area of about 450 km2. The geoglyphs depict animals, plants, imaginary beings, and geometric figures that are several kilometres long.
Parallel lines and other geometric shapes are featured in many ancient and modern designs. These shapes may exist on their own or be part of a larger pattern. The designs rely on the lines being parallel in order to have a successful, aesthetically pleasing final product. Determining how the parallel lines can be constructed is an important component of the design process.
An understanding of geometry including angle properties and parallel lines is very useful when creating or examining geometric designs. For example, precise theoretical and working knowledge of geometry was needed to build the Nazca lines in Peru. These huge geometrical designs can only be viewed from the air. The designs would have been impossible to create without an understanding of geometry and careful prior planning.
—Emory Dean Keoke, Kay Marie Porterfield. Encyclopedia of American Indian Contributions to the World. (Facts on File, 2001.) pp. 118-119.
Archaeologists require an understanding of how parallel lines can be constructed to solve problems involving the creation of ancient designs. Being able to tell whether the lines in the design are parallel or non-parallel can also provide useful information on their potential function.
This lesson will help you answer the following inquiry questions:
- How can different strategies be applied to construct parallel lines?
- How can the properties of angles formed by parallel lines and a transversal be used to solve problems?
Assessment
- Try This 2
- Lesson 8 Assignment
All assessment items you encounter need to be placed in your course folder.
Save a copy of the Lesson 8 Assignment to your course folder. You will receive more information about how to complete the assignment later in this lesson.
Materials and Equipment
1.1. Launch
Module 2: Logic and Geometry
Launch
Refresher
In this lesson you will be working with a protractor and compass. You may wish to review using a protractor. If so, you can access the following tutorials:
Under the Shape and Space heading, go to “Angles–Construct and Measure (Perspectives).” Choose “Topics.” Then choose the following:
- “Topic 3: Measuring Angles with a Protractor”
- “Topic 4: Using the Protractor”
- “Topic 6: Creating Angles”
To review how to construct a perpendicular bisector using a compass, watch the animation Process to Construct a Perpendicular Bisector. Recall that a perpendicular bisector is a line or line segment that both bisects a given line segment and is perpendicular to it.
1.2. Discover
Module 2: Logic and Geometry
Discover
Think about some items in your everyday life that contain parallel lines. How would the look of these items change if the lines were not quite parallel? Think about your favourite pair of striped socks, a referee’s shirt, or the Canadian flag. The overall look and appeal of these items would change if the lines in their design were not parallel.

Photos.com/Thinkstock

Hemera/GettyImages/Thinkstock

Alberta Economic Development
This is true for designs on a larger scale as well. For instance, when designing a corn maze, it is important that the lines of the maze are parallel to each other. If the lines are not parallel, the paths may cross over each other at some point. This has the potential to change the desired path of the maze. Think about how this also relates to the lines on roads. It would not be very safe if the width of the lanes kept changing because the centre yellow line was not parallel to the outside white lines.

Alberta Economic Development
1.3. Discover 2
Module 2: Logic and Geometry
Try This 1
Pretend you are designing a logo for a T-shirt that will have two parallel lines on it. How could you construct two parallel lines on the design for the logo using a compass and a ruler or a protractor and a ruler? Explain the strategy you used and why you chose that method. Verify that the lines you created are parallel.

Share 1
Working with a partner, discuss your strategy for constructing two parallel lines. In your discussion consider the following questions:
- How do your strategies compare?
- Is one strategy more efficient than the other?
- Do both methods produce parallel lines? If not, how could the strategy be adapted so that the lines constructed are parallel?

Hemera/Thinkstock
1.4. Explore
Module 2: Logic and Geometry
Explore
The strategies used to construct and then verify that lines are parallel in a design will vary. For instance, different strategies could be used to construct parallel lines on a blanket versus parallel lines in a corn maze.

Alberta Economic Development
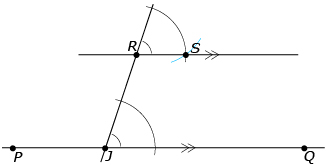
When Jarjeet was asked to construct a set of parallel lines for his T-shirt logo in Try This 1, he decided to use a compass and a ruler. At this time, type the keywords “constructing a parallel through a point” into your favourite Internet search engine. This search should take you to a page at the Math Open Reference website.
This strategy works by using the corresponding angles property. Recall that when a transversal intersects two parallel lines, it creates pairs of corresponding angles that are equal in measure. In this strategy, two equal corresponding angles are created first with the compass. These angles are then used to identify the location of line RS. Using the ruler or straightedge to draw a line through points R and S creates the line that is parallel to the original line—line PQ.
Self-Check 1
- Complete “Practising” question 4 on page 85 of your textbook. You may find it helpful to review Parallelogram. Answer
- Complete “Practising” question 6 on page 79 of your textbook. Answer
1.5. Explore 2
Module 2: Logic and Geometry
Lesson Assignment
Complete question 1 of your Lesson 8 Assignment that you saved to your course folder. Then resave your updated Lesson 8 Assignment to your course folder.
Geometric designs containing parallel lines are evident in many cultures. These designs can be found in paintings on rocks, etchings in the ground, baskets, pottery, textiles, beadwork, and ceremonial pieces. For example, in the Democratic Republic of the Congo, the Mangbetu women wore pieces of barkcloth that were decorated with geometric patterns like the one shown.

Did You Know?
The Mangbetu ideal of feminine beauty included painting the body in geometric patterns. The women of the ruling class painted their bodies with a black juice made from the gardenia plant.
— Paulus Gerdes. Geometry from Africa: Mathematical and Educational Explorations. (Washington: Mathematical Association of America, 1999). Pp. 25, 29.
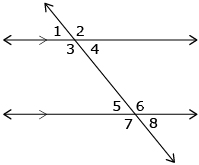
To create a successful final product, some designs need the lines to be parallel. Designers can verify that the lines they construct in their designs are parallel by measuring the angles formed by the lines and a transversal. A review of the angle relationships formed when a transversal intersects two parallel lines is provided on the right. Remember, it does not matter if the lines look parallel; they have to be parallel for the angle properties to apply.
The lines are parallel if a transversal intersects two lines and the following occurs:
- the corresponding angles are equal: ∠1 = ∠5, ∠2 = ∠6, ∠3 = ∠7, ∠4 = ∠8
- the alternate exterior angles are equal: ∠1 = ∠8 and ∠2 = ∠7
- the alternate interior angles are equal: ∠3 = ∠6, ∠4 = ∠5
- the interior angles on the same side of the transversal are supplementary: ∠3 + ∠5 = 180°,
∠4 + ∠6 = 180°
Consider the following situation. Akono is taking a pottery class. One of his projects is to decorate a serving plate with a geometric design. He decided to use a pattern he found in his research that was used to decorate gourds in Nigeria.
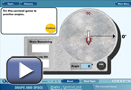
Akono wants to check that the lines he constructed on his serving plate are parallel. Using a protractor, Akono measures some of the angles on the completed plate. Watch the animation Measuring Angles in Akono’s Design to see the angle measurements.
Akono’s reasoning used the property of corresponding angles to prove that the lines that he selected in his design are parallel.
1.6. Explore 3
Module 2: Logic and Geometry
Try This 2
Go to the Lesson 8 Assignment that you saved to your course folder. Complete Try This 2 at this time. Remember to save your updated Lesson 8 Assignment to your course folder when you have completed Try This 2.
Given that the lines shown in Akono’s design are parallel, determine the measure of the unknown angles in the following diagram. Justify your decisions. (4 marks)
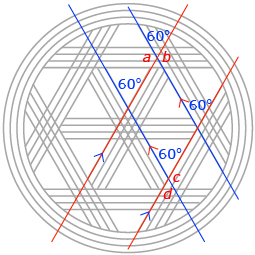
If you need some help determining where to start, read “Example 2: Using reasoning to determine unknown angles” on page 76 of your textbook.
Self-Check 2
Complete “Practising” questions 5 and 8 on page 85 of your textbook. Answer
1.7. Explore 4
Module 2: Logic and Geometry
Lesson Assignment
© Hocoma. Reproduced with permission.
If the lines in a design or final product are not parallel but are supposed to be, the design or final product has to be adapted or changed. Think about the consequences of a set of parallel bars used to help rehabilitate a patient that have not been setup parallel. It is crucial that the bars are actually parallel to one another. The safety of the patients depends on it.
Barbara is an occupational therapist. One of her responsibilities is to ensure that the parallel bars used by patients are actually parallel. Her preferred strategy is to lay a metre-stick across the top of the bars. She then measures some of the angles formed when the metre-stick intersects the bars. Barbara checks for accuracy by moving the metre-stick to a different position and having it intersect the bars at a different angle. A sketch of her measurements is shown.
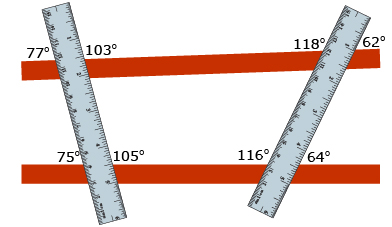
Barbara believes that, based on her angle measurements, the bars are parallel to one another.
1.8. Explore 5
Module 2: Logic and Geometry
Try This 3
- Use the animation Adjusting Parallel Bars to verify or to disprove Barbara’s conjecture that the bars are parallel.
- How could Barbara verify that the bars are parallel with the floor as well as each other?

Self-Check 3
- Complete “Practising” question 7 on page 85 of your textbook. Answer
- Complete “Closing” question 19 on page 82 of your textbook. Answer
If you want to challenge your understanding of the angle properties using algebra, try Self-Check question 3.
- Try “Extending” question 21 on page 82 of your textbook. Answer
1.10. Lesson 8 Summary
Module 2: Logic and Geometry
Lesson 8 Summary

Alberta Economic Development
Ukrainian dancers perform in front of the world’s largest Ukrainian Easter egg at Vegreville. This roadside attraction, also called the Pysanka, was built in 1975 to commemorate the community’s Ukrainian heritage.
Parallel lines are used in a variety of situations. They are found in geometric designs on clothing and pottery. Parallel lines can be found in artifacts or scratched into the ground or rock at ancient sites.
An understanding of the properties of angles formed by parallel lines and a transversal is very useful when creating or examining geometric designs. For example, these angle properties can be used to help develop a strategy for constructing parallel lines with a protractor or a compass.
The angle properties can also be used to prove lines are parallel or to determine the measures of unknown angles. If lines are not parallel, an understanding of the angle properties allows you to identify errors and determine why the lines are not parallel. This information can then be used to develop a strategy for making the lines parallel.
You will use the properties of angles formed when a transversal intersects parallel lines to solve problems involving triangles in Lesson 9.