Lesson 9
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-2 SS |
| Book: | Lesson 9 |
| Printed by: | Guest user |
| Date: | Tuesday, 30 December 2025, 9:53 AM |
Description
Created by IMSreader
1. Lesson 9
Module 2: Logic and Geometry
Lesson 9: Proving Angle Properties in Triangles
Focus
Martin Gardner (1914–2010) was known as the Mathematical Gamester. Gardner published a number of books of puzzles, problems, and mathematical games. One brain teaser found in his books was developed by Mel Stover of Winnipeg and is called Acute Dissection.
—Philip Yam. “Profile: Martin Gardner, the Mathematical Gamester (1914–2010),” Scientific American,
22 May 2010, <http://www.scientificamerican.com/article.cfm?id=profile-of-martin-gardner&page=4>;
(17 February 2011).

Creatas/Thinkstock
The problem asks whether it is possible to cut any triangle with one obtuse angle into smaller, acute triangles. If it cannot be done, a proof of impossibility is required. If it can be done, the solution must show the smallest number of acute triangles that an obtuse triangle can be dissected into.
—Martin Gardner. My Best Mathematical and Logic Puzzles. (Mineola, NY: Dover Publications, 1994)
To solve this problem, an understanding of angles and triangles is required. You know from previous courses that acute triangles have angles that are less than 90°. Obtuse triangles have one angle that is greater than 90°.
Another theorem you have been told in previous courses is that the sum of the three interior angles in a triangle is 180°. You have been given this theorem, but are you 100% sure that the sum of the interior angles in a triangle will always be 180°?
This lesson will help you answer the following inquiry questions:
- How can properties of angles in triangles be proven using deductive reasoning?
- How can the properties of angles in triangles be used to solve problems?
Assessment
- Lesson 9 Assignment
All assessment items you encounter need to be placed in your course folder.
Save a copy of the Lesson 9 Assignment to your course folder. You will receive more information about how to complete the assignment later in this lesson.
Materials and Equipment
1.1. Discover
Module 2: Logic and Geometry
Discover
Joe is teasing his brain with the Acute Dissection problem. He dissects the obtuse triangle into four smaller triangles as shown in the diagram. Then he uses a protractor to measure all of the angles. Joe concludes that since the four triangles in his diagram all have sums of 180°, then all triangles have sums of 180°. The following is what Joe considers his proof.
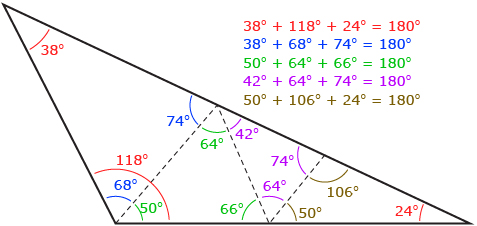
Is Joe’s evidence enough to prove that the sum of the interior angles in a triangle is 180°?
Joe used inductive reasoning in his solution. From previous lessons, you know that inductive reasoning cannot be used to prove a conjecture. The evidence Joe gathered strengthens the conjecture that the sum of the angles in a triangle is 180°, but it does not prove the conjecture.
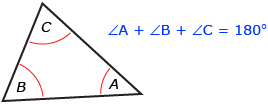
The sum of the interior angles of a triangle theorem may be one of the most well-known mathematical theorems. In previous courses you have been told that the sum of all three interior angles in a triangle is 180°, but you may never have proven that this is true for all cases.
In fact, in previous courses, you might even have folded the corners of a triangle together to show that all three interior angles of a triangle form a line.
Use the Interactive Triangle applet or the Folded Paper Triangle applet to investigate the sum of the interior angles of a triangle. In each applet, you can drag a vertex of the triangle to make triangles of varying sizes. As you change the triangles, does the sum of the angles in the triangles change?
The Interactive Triangle applet and the Folded Paper Triangle applet both illustrate that the sum of the interior angles of a triangle is 180°. But why is this? What is the reasoning behind this theorem? In the following Try This activity, you will prove that the measures of the three angles in any triangle—acute, right, and obtuse—have a sum of 180°.
Try This 1
Complete “Investigate the Math” problems A to H on pages 86 and 87 of your textbook. You can draw your triangles on paper using dynamic geometry software or another method of your choice.
Make sure line PQ is parallel to line RE in your drawing.
1.2. Explore
Module 2: Logic and Geometry
Explore
In Discover you used the properties of angles formed by a transversal intersecting two parallel lines to prove the sum of the measures of the interior angles in a triangle is 180°. Watch the animation Proving the Sum of Interior Angles to see a proof developed by one student, Zahia.
If the proof you created in Try This 1 was invalid, go back to your original drawing. Make sure your lines are parallel. Remember that the properties of angles are only true when a transversal intersects two parallel lines, not two non-parallel lines.
As you have seen in previous lessons, deductive proofs can be created in many forms. The proof shown in the animation Proving the Sum of Interior Angles of a Triangle was presented as a series of statements that explained the student’s reasoning process. The reasoning could have also been presented in a two-column proof.
Given: ![]()
Prove: ∠DRE + ∠RDE + ∠RED = 180°
Proof:
|
Statements |
Justifications |
|
1. Draw |
A line can be drawn parallel to a given line through an external point not on the line. |
|
2. ∠PDQ = 180° |
A straight line angle measures 180°. |
|
3. ∠PDR + ∠RDE + ∠QDE = 180° |
The three angles form a straight line, so their sum is 180°. |
|
4. ∠DRE = ∠PDR and ∠RED = ∠QDE |
Alternate interior angles. |
|
5. ∠DRE + ∠RDE + ∠RED = 180° |
Substitution (a quantity may be substituted for an equal quantity). |
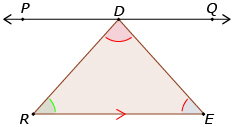
Therefore, the sum of the interior angles in a triangle is always 180°.
Regardless of the method, diagrams are useful to include in proofs as they provide a visual of the situation.
1.3. Explore 2
Module 2: Logic and Geometry
Self-Check 1
- Complete “Check Your Understanding” questions 1 and 2 on page 90 of your textbook. Answer
- Complete “Practising” question 6 on page 85 of your textbook. Answer
Now that you have proven that the sum of the interior angles in a triangle is always 180°, you can use this relationship (and other relationships that you already know) to determine
- unknown angles measures
- relationships between other angles
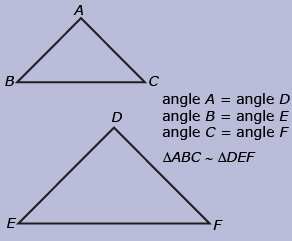
The symbol ~ represents similar to. When two triangles are similar, they are the same shape (i.e., the angles are the same) but are different sizes.
1.4. Explore 3
Module 2: Logic and Geometry
Try This 2
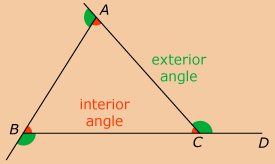
exterior angle: an angle at a vertex of a triangle, outside the triangle, formed by one side and the extension of an adjacent side
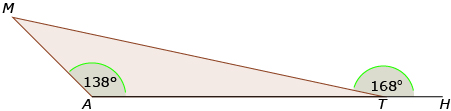
Determine the measures of the unknown angles in ![]() . Note that ∠MTH is an exterior angle of
. Note that ∠MTH is an exterior angle of ![]() . Justify your reasoning.
. Justify your reasoning. ![]()
Share 1
Use your angle measurements from Try This 2 to answer the following questions with another student.
- Compare your angle measurements from Try This 2 with your partner’s measurements.
- Did you get the same answers for the unknown angle measurements?
- How were your methods for determining the unknown angles similar? How were they different?
- Did you get the same answers for the unknown angle measurements?
-
With your partner, make a conjecture about the relationship between an exterior angle (∠MTH) and its two non-adjacent interior angles (∠AMT and ∠MAT) based on your results.
non-adjacent interior angles: two angles of a triangle that do not have the same vertex as an exterior angle

1.5. Explore 4
Module 2: Logic and Geometry
In the preceding Share activity, you and your partner were asked to make a conjecture about the relationship between an exterior angle and its two non-adjacent interior angles. Zahia and her partner made the following conjecture.

iStockphoto/Thinkstock
Use the Exterior Angles of Triangles applet to see if Zahia’s conjecture holds true for other triangles. Drag the orange dots on any vertex to reshape the triangle.
The Exterior Angles of Triangles applet illustrates the relationship between the exterior and interior angles of a triangle. Read “Example 2: Using reasoning to determine the relationship between the exterior and interior angles of a triangle” on page 88 of your textbook to see a proof of this relationship. As you read through Joanna’s proof, consider how she uses angle properties you have learned in previous lessons to prove the relationship between an exterior angle of a triangle and the two non-adjacent interior angles.
Self-Check 2
1.6. Explore 5
Module 2: Logic and Geometry
Lesson Assignment
Complete questions 1 and 2 of the Lesson 9 Assignment that you saved to your course folder. Once you have completed the first two questions, save your updated document to your course folder and continue with this lesson.
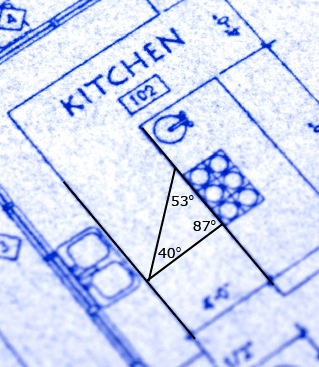
In Lesson 8 you looked at various geometric designs that contained parallel lines. Many designs used in quilting, manufacturing, and architecture also contain triangles as well as parallel lines. For example, when designing a kitchen, parallel lines and triangles are used to determine the best placement of cabinetry and appliances. In fact, the kitchen work triangle is recognized by most designers as an effective and efficient layout for a kitchen. The vertices of the kitchen work triangle are the fridge, stove, and sink.
Comstock/Thinkstock
Consider the following situation.
Howard is a supervisor for a kitchen design company. One of his new designers has just e-mailed him a plan for a kitchen that highlights the kitchen work triangle. Before the plans are passed onto the construction crew, Howard needs to verify that the row of cabinets and the centre island are parallel to one another. Howard knows that mistakes are much easier and less costly to fix at the design stage than after construction has started.
Howard is currently on a job site and cannot print a copy of the e-mail. He does not have access to a protractor or a ruler to verify the measurements anyways. The construction supervisor is waiting for the plans, so Howard decides to use his understanding of the angle properties to verify that the row of cabinets is parallel to the island in the kitchen design drawing.
1.7. Explore 6
Module 2: Logic and Geometry
Try This 3
Use the applet titled Kitchen Triangle to help Howard verify that the row of cabinets is parallel to the island. There are several different strategies you can use to solve this problem. Using the applet, identify at least three different strategies Howard could use. Record your strategies and place them in your course folder.
Share 2
- Compare your three proofs from the Kitchen Triangle applet with another student. Did you use the same methods? Did all of the methods you and your partner used prove that the cabinets were parallel to the island?
- After sharing with another student, do you see a simpler method to verify that the row of cabinets is parallel to the island? Is there one strategy you prefer over the others? Explain why.
1.8. Explore 7
Module 2: Logic and Geometry
The properties of angles can be used to solve problems. As you have seen, sometimes the properties can be combined in different ways to solve the same problem. As long as the reasoning used is correct and you have applied the angle properties correctly, many strategies will give a correct solution to the problem. You will find that some strategies may be more efficient than others; e.g., some strategies may require fewer steps. It is important to understand that the key to solving problems involving angle properties is to use strategies that apply correct methods and reasoning regardless of how many steps are required.
Read “Example 3: Using reasoning to solve problems” on pages 88 and 89 of your textbook to see personal strategies Tyler and Dominique used for solving the same problem. As you read over their solutions, consider the following questions.
- Which of the two strategies shown in the textbook do you prefer?
- Do you see a strategy you like better than the strategies used by Tyler and Dominique?
- Think about the strategy you prefer. Are there angle relationships you find easier to identify? Do you prefer working with angles in triangles? Do you prefer working with angles related to parallel lines?
Remember that your strategy may differ from others, but as long as you apply the angle properties correctly and use correct reasoning, you can still find the same solution to a problem.
Self-Check 3
Complete “Practising” questions 11, 12, 13, and 15 on page 92 of your textbook. Answer
If you haven’t done so already, now is a good time to update your notes organizer. A good starting point is to reflect on how drawing a line that is parallel to one side of any triangle can help you prove that the sum of the angles in a triangle is 180°. You may find the ideas presented in the “In Summary” section on page 90 of your textbook useful.
1.9. Connect
Module 2: Logic and Geometry
Connect
Lesson Assignment
Complete the Lesson 9 Assignment that you saved to your course folder.
Going Beyond
In the Focus section of this lesson you were presented with a brain teaser called Acute Dissection. Recall that the problem asks whether it is possible to cut any triangle with one obtuse angle into smaller, acute triangles. If it cannot be done, a proof of impossibility is required. If it can be done, the solution must show the smallest number of acute triangles that an obtuse triangle can be dissected into.
—Adapted from Gardner’s “My Best Mathematical and Logic Puzzles” ISBN 0-486-28152-3.
The triangle that Joe presented at the start of this lesson is not a correct solution. One of his triangles is obtuse.
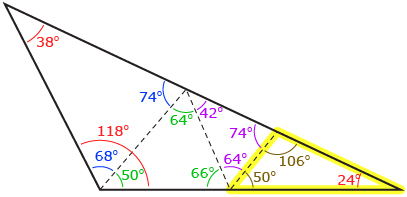
Can you solve this problem? Answer
1.10. Lesson 9 Summary
Module 2: Logic and Geometry
Lesson 9 Summary
Hemera/Thinkstock
The theorem that the sum of the interior angles in a triangle is 180° has been given to you in previous math courses. In this lesson you applied the properties of angles you learned in this module to prove that the sum of the interior angles in a triangle is 180°.
The properties of angles are useful for solving problems. As you have seen, many items in design involve triangles and parallel lines. An understanding of how the properties of angles can be used to determine that two lines are parallel can be used to verify design plans. In some instances, the properties can be combined in a variety of ways to solve the same problem.
In Lesson 10 you will continue to work with properties of angles. This time, you will use the properties of angles to prove that two triangles are congruent.