Lesson 10
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-2 SS |
| Book: | Lesson 10 |
| Printed by: | Guest user |
| Date: | Tuesday, 30 December 2025, 9:47 AM |
Description
Created by IMSreader
1. Lesson 10
Module 2: Logic and Geometry
Lesson 10: Congruent Triangles
Focus

iStockphoto/Thinkstock
The National Gallery of Canada building in Ottawa contains both similar and congruent triangles in its roof design. The smaller congruent triangular windows at the top of the building fill a larger similar triangular steel frame. For the smaller triangles to be congruent, the lengths of the corresponding sides and the measures of the corresponding angles of each of the smaller triangles must be the same. For the two sizes of triangles to be similar, the length of the sides of the larger triangular steel frame have to be proportional to the smaller triangles and the angle measures have to be the same.
When items are part of a larger design, such as the windows in the National Gallery of Canada, it is crucial that all the necessary measurements are provided to the manufacturers. If the manufacturer is not given enough information, the design will not be accurately reproduced.
For instance, the company that made the windows for the National Gallery of Canada had to have enough information to ensure that every window constructed was congruent. If the notes were not the same, the smaller triangles would not have fit into the larger steel frame. The entire construction process would have been affected, and the overall design would not have worked.
This lesson will help you answer the following inquiry questions:
- What is the minimum amount of information needed to create two triangles that are congruent?
- How can deductive reasoning be used to prove that triangles are congruent?
Assessment
- Try This 2
All assessment items you encounter need to be placed in your course folder.
Save a copy of the Lesson 10 Assignment to your course folder.
Materials and Equipment
1.1. Launch
Module 2: Logic and Geometry
Launch
Recall that two triangles are congruent if all corresponding sides are equal and all corresponding angles are equal. To state it simply: corresponding sides must have the same length and corresponding angles the same measure. For example, the following two triangles are congruent (e.g., the same).
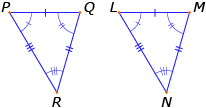
PQ = LM
QR = MN
PR = LN
and
∠P = ∠L
∠Q = ∠M
∠R = ∠N
![]()
![]()
Congruent triangles do not need to have the same orientation. A triangle can be transformed by a translation, rotation, or reflection and the result will still be a congruent triangle.
1.2. Are You Ready?
Module 2: Logic and Geometry
Are You Ready?
In previous mathematics courses you learned about similar and congruent triangles. To check your understanding of the difference between similar shapes versus congruent shapes, use the “Exploring Similarity and Congruence” applet at the LearnAlberta website. Click on the “Interactive” button on the left-hand side of the screen to begin.
1.3. Refresher
Module 2: Logic and Geometry
Refresher
For more information on similarity and congruence, return to “Exploring Similarity and Congruence.” Click on “Video” on the left-hand side of the screen. This video shows examples of similar and congruent triangles used in the construction of road signs. As you watch the video, think about what makes two shapes congruent versus what makes two shapes similar. Think about the relationship between their sides and angles.
Contact your teacher if you feel you need more help with this concept.
1.4. Discover
Module 2: Logic and Geometry
Discover
To construct the windows for the roof of the National Gallery of Canada, the manufacturer needed accurate measurements. For the rectangular windows, only two measurements were needed. The manufacturer needed to know the length and width of the rectangular windows in order to create congruent rectangles. To construct the triangular windows, six measurements could have been provided—three side lengths and three angles. But are all six measurements required to construct congruent triangles?
Actually, the manufacturer only needed to know three measurements to create the congruent triangles for the gallery’s roof. There are several different combinations of three measurements that could have been given to the manufacturer.
- side-side-side (SSS)
- side-side-angle (SSA)
- side-angle-side (SAS)
- angle-side-angle (ASA)
- angle-angle-side (AAS)
- angle-angle-angle (AAA)
Not all of these combinations of measurements will guarantee that a congruent triangle is produced. So which three measurements must be given to the manufacturer in order to produce congruent triangles?
Try This 1
Use the applet Creating Congruent Triangles to see triangles created given AAS and AAA.
The applet Congruent Triangles Manipulative1 can be used to create triangles given SSS, SAS, ASA, and SSA.
Use the information you collect from these two applets to answer the following questions.
- Which combination(s) of given side and angle measurements ensure that all the triangles produced are congruent?
- Which combination(s) of given side and angle measurements do not ensure that the triangles are congruent? (Is it possible to construct two non-congruent triangles with some combinations of sides and angles?)
Self-Check 1
Based on your findings from Try This 1, complete the Congruent Triangle Table.
1 National Library of Virtual Manipulatives. © 2011 Utah State University
1.5. Explore
Module 2: Logic and Geometry
Explore
When designing structures that contain congruent triangles, there is a minimum set of angle and side measurements that can be given to ensure that the triangles constructed are the same. Remember that two or more triangles are congruent if their corresponding sides are equal in length and their corresponding angles are equal in measure.
In Discover you showed that a minimum of three sets of measurements is required in order to establish congruency:
- SSS (side-side-side): If three pairs of corresponding sides are equal in length, then the triangles are congruent.
AC = DF
BC = EF
AB = DE
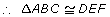
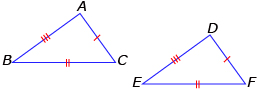
- SAS (side-angle-side): If two pairs of corresponding sides are equal in length, and the included angles are equal in measure, then the triangles are congruent.
AB = DF
∠B = ∠E
BC = EF
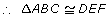
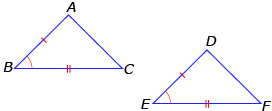
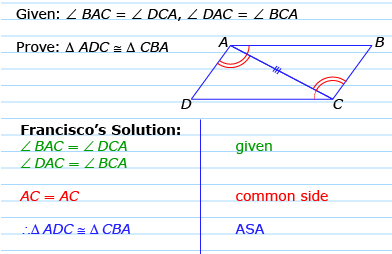
- ASA (angle-side-angle): If two pairs of corresponding angles are equal in measure and the included sides are equal in length, then the triangles are congruent.
∠B = ∠E
BC = EF
∠C = ∠F
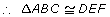
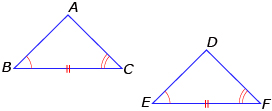
- AAS (angle-angle-side): If two pairs of corresponding angles are equal in measure and a pair of opposite sides is equal in length, then the triangles are congruent.
∠B = ∠F
∠C = ∠F
AB = DE
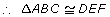
Not all mathematicians agree that AAS is a condition of congruency. Some believe that this is a special application of ASA. They support this statement as follows:
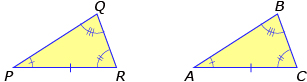
In order to have angle-angle-side (AAS) congruent, the third angle must also be congruent. By changing which angles to compare, ASA congruency is proved. Consider ![]() and
and ![]() . Since ∠Q = ∠B, ∠P = ∠A, and PR = AC, then ∠R = ∠C. ASA congruency would mean that ∠P = ∠A, PR = AC, ∠R = ∠C. Therefore,
. Since ∠Q = ∠B, ∠P = ∠A, and PR = AC, then ∠R = ∠C. ASA congruency would mean that ∠P = ∠A, PR = AC, ∠R = ∠C. Therefore, ![]() because of ASA.
because of ASA.
As such, for this course, you should not use AAS as a condition of congruency. Instead, you need to find the third angle and use ASA as a condition of congruency.
You also showed that not all combinations of measurements will guarantee that two congruent triangles will be produced from the given information.
- AAA: When given three angle measurements, triangles of the same shape but different sizes can be created. These triangles are similar but not necessarily congruent. So, AAA does not provide enough information on its own to guarantee that two triangles are congruent.
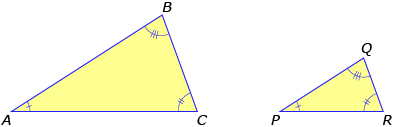
- SSA: More than one triangle can be constructed when given the length of two sides and a non-included angle. So on its own, SSA is not enough information to guarantee congruency.
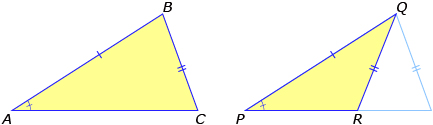
1.6. Explore 2
Module 2: Logic and Geometry
Self-Check 2
Complete “Further Your Understanding” questions 2, 3, and 4 on page 106 of your textbook. Answer
In previous lessons you have used deductive reasoning to prove elements of designs, such as pairs of parallel lines. Deductive reasoning can also be used to prove that two triangles are congruent. The steps involved in proving that two triangles are congruent are similar to the steps involved in proving two lines are parallel.
To prove that two triangles are congruent, you first need to analyze the given information. Then, through a series of statements and reasons, you can develop your proof. The minimum set of angle and side measurements required to ensure that triangles are congruent can be used to help build your proof. Remember that in order for the proof to be valid and understood by others, the reasoning must be presented in a logical and clear way.
Consider the following situation.
Did You Know?
Fractals are shapes that are made up of smaller copies of the original shape. The copies are similar; they have the same shape but different sizes. For more information on fractals, including fractal puzzle makers, search the term “fractal” on your favourite Internet search engine.
Lisbeth has been trying to recreate the Sierpinski Triangle pattern shown here. This pattern is an example of a fractal. To build Sierpinski’s Triangle, start with an equilateral triangle with a side length of one unit (see Figure 1). The triangle is then divided into four triangles by finding the midpoint of each side and then connecting the midpoints. The middle triangle is then cut out (see Figure 2). This process is repeated to produce the remaining figures.


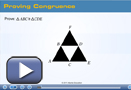
In Figure 2, the pattern is made up of four small triangles and one large triangle. Lisbeth knows that in order for the pattern to continue on successfully, the smaller triangles have to be congruent. She decides to use her knowledge of triangles and angle properties to prove that the two bottom black triangles are congruent.
Watch the animation Proving Congruence to see how Lisbeth builds her proof. As you work through Lisbeth’s proof, think about the importance of updating diagrams as you progress through a proof.
The pairs of sides and angles that are chosen to prove congruence depends on the information given and other relationships that you can deduce.
Share 1
With a partner, explain another way to prove that the triangles in the Sierpinski Triangle pattern are congruent.
Deductive reasoning can also be used to prove the classification of triangles. For instance, reasoning can be used to prove that a triangle is an isosceles or equilateral triangle. Deductive reasoning can also be used to prove that parts of triangles are equal.
1.7. Explore 3
Module 2: Logic and Geometry
Read “Example 2: Reasoning about congruency to prove that sides are equal” and “Example 3: Reasoning about congruency to prove that angles are equal” on pages 109 and 110 of your textbook. As you read over the solutions, consider the following questions.
- How is deductive reasoning used to prove that the triangle is isosceles in Example 2?
- What characteristics of an isosceles triangle were required to build the proof?
- Why did each pair of triangles first have to be proven congruent before the students could prove that
 is isosceles and that ∠A = ∠E?
is isosceles and that ∠A = ∠E?
Example 2 shows that it is helpful to keep in mind what it is you are trying to prove when building your proofs. For instance, to prove that the triangle is isosceles, you have to understand what characteristics make a triangle isosceles: two congruent sides and two congruent angles. These then become the parts you have to prove.
Self-Check 3
1. Complete “Your Turn” on page 109 of your textbook. Answer
2. Complete “Your Turn” on page 110 of your textbook. Answer
3. Complete “Practising” questions 4, 5, and 6 on page 113 of your textbook. Answer
1.8. Explore 4
Module 2: Logic and Geometry
Try This 2
You will submit your answer for Try This 2 to your teacher for marking.
You can answer Try This 2 in the Lesson 10 Assignment that you saved to your course folder.
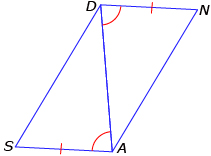
Parallelograms are quadrilaterals with opposite sides that are parallel. Given that SA = ND and ∠SAD = ∠NDA, prove that SAND is a parallelogram. (5 marks)
1.9. Explore 5
Module 2: Logic and Geometry
Did You Know?
The National Gallery of Canada website has a virtual exhibition that contains some of the work of artist
M. C. Escher. The exhibit M.C. Escher Mindscapes contains examples of Escher’s work including his tessellations. M. C. Escher used the laws of geometry to create tessellations that fill entire sheets with recognizable and identical forms. Type the keyword “tessellation” or “M.C. Escher” into your favourite Internet search engine to see more examples of tessellations.
The National Gallery of Canada and the pyramid at the entrance to the Louvre Museum in France both contain tessellations in their building designs. Tessellations are arrangements of figures on a plane that completely cover a surface without gaps or overlaps. They are repeating patterns created by a series of translations, reflections, or rotations of polygons. Only polygons whose interior angles add up to 360° or a multiple of 360° will tessellate.

Hemera/Thinkstock
Read “Example 4: Reasoning about congruency to prove an angle relationship” on pages 110 and 111 of your textbook. Two strategies for proving that the base angles on each face of the Louvre pyramid are equal are provided. After you have worked through each student’s solution shown in your textbook, think about which strategy you prefer and why you prefer that strategy. Remember that both strategies give the same answer, so one is not more correct than the other. You must decide which strategy works for you in each question. Be sure to check your work to ensure you have correctly applied the angle properties and used correct reasoning.
Depending on the information given, there may be a number of approaches that can be used to complete a proof. For instance, properties relating to angles and parallel lines, triangles, and circles may be used to develop a proof. Remember back to your Mathematics 9 course. You studied angles relating to circles. You can also use these angle properties in developing your proofs.
Consider the following.

Marie-Josie is a stained glass artist. A client has asked her to create a stained glass window based on the following design. One of the client’s requirements is that the two triangles used in the design are the same.
Before Marie-Josie begins construction of the stained glass window, she needs to verify that the two triangles provided by her client are in fact congruent. Use the applet Stained Glass Proof to view and then analyze Marie-Josie’s proof.
As you have seen throughout this module, errors in reasoning result in invalid proofs. If the errors are not fixable, then the proof is not valid. If the errors can be corrected, a valid proof can be produced.
The two triangles in Marie-Josie client’s stained glass design were not congruent. In this case, the error in reasoning could not be fixed to prove that the triangles were the same because the triangles were not congruent. Additional information about the side lengths of the triangle would have shown that the triangles were not congruent. Marie-Josie needs to go back to her client with a design that she can prove contains congruent triangles.
1.10. Explore 6
Module 2: Logic and Geometry
Self-Check 4
Complete “Practising” questions 9, 10, 14, and 16 on pages 114 and 115 of your textbook. Answer
Try This 3
Use the applet Mark’s Proof to identify Mark’s error and correct the proof.
Self-Check 5
If you feel you need some more practice identifying and correcting errors in a proof, complete “Practising” question 11 on page 114 of your textbook. Answer
1.11. Lesson 10 Summary
Module 2: Logic and Geometry
Lesson 10 Summary
If a design is based on congruent triangles, it is crucial that all the triangles in the design are in fact congruent (the same). If they are not the same, the overall design can be negatively affected. There is a minimum set of angle and side measurements that can be given to ensure that the triangles constructed are the same. To establish congruency, a minimum of three sets of measurements is required:
- SAS (side-angle-side): If two pairs of corresponding sides are equal in length, and the included angles are equal in measure, then the triangles are congruent.
- SSS (side-side-side): If three pairs of corresponding sides are equal in length, then the triangles are congruent.
- ASA (angle-side-angle): If two pairs of corresponding angles are equal in measure and the included sides are equal in length, then the triangles are congruent. If two pairs of corresponding angles are equal in measure and a pair of opposite sides is equal in length AAS (angle-angle-side), you need to find the third angle and use ASA as a condition of congruency.
These sets of angle and side measurements can be used to prove that triangles are congruent. Deductive reasoning can also be used to prove the classification of triangles or to prove that parts of triangles are equal. Solving these problems requires first proving that the triangles are congruent.
In order for proofs to be valid and understood by others, statements and justifications must be presented in a logical and clear manner. Any errors or unclear steps will result in an invalid proof.
In the final lesson in this module, Lesson 11, you will apply your knowledge of the properties of angles to polygons and then analyze and create your own design.