Lesson 11
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-2 SS |
| Book: | Lesson 11 |
| Printed by: | Guest user |
| Date: | Tuesday, 30 December 2025, 9:48 AM |
Description
Created by IMSreader
1. Lesson 11
Module 2: Logic and Geometry
Lesson 11: Reasoning to Solve Design and Layout Problems
Focus
Dome-shaped structures have been used in the construction of stadiums, homes, and even for research facilities that are built in some of the harshest climates in the world. Probably one of the most recognizable dome-shaped structures in Canada is the igloo. The igloo is known for its dome and its ability to protect those inside from the cold. The architecture of an igloo uses materials found in nature to suit human needs.

© Tyler Olson/6948788/Fotolia
Did You Know?
The spiral structure of a dome is one of the most efficient interior atmospheres for human dwellings. Air and energy can move without obstruction, so heating and cooling occurs naturally. A well-built igloo with a soapstone lamp could bring the temperature up to around 0°C even when it is −40° outside.
—CBC.ca

iStockphoto/Thinkstock
The energy-efficient design of the dome is recognized by many architects and designers. Because of its decreased surface area, construction of a dome requires less building materials. A dome shape is also well suited to large arenas and stadiums. It can enclose more space without using support columns that get in the way.
The use of polygons in design requires careful planning and knowledge of how polygons can be arranged to fit together. For instance, when constructing an igloo, the angles of each block are based on its position in the structure. The blocks have to be shaped so that they lean inward to create the dome but still fit snuggly with the blocks above and below them. If the angles in the blocks are not correct, the igloo will collapse.
An understanding of angles in polygons helps designers, artists, and architects visualize patterns and produce successful designs.
This lesson will help you answer the following inquiry questions:
- What relationships can be identified between angles and sides in polygons?
- How can the properties of angles and polygons be used to solve design and layout problems?
Assessment
- Try This 3
- Module 2 Project
All assessment items you encounter need to be placed in your course folder.
Materials and Equipment
1.1. Discover
Module 2: Logic and Geometry
Discover

iStockphoto/Thinkstock
The use of polygons in design and architecture is not a modern phenomenon. Polygons have been used for centuries in art and architectural details. In many cultures, polygons have symbolic meaning. Some designs and artifacts are even classified as sacred geometry. Polygons were also used when designing items for daily life. Master weavers and tilers used polygons to create illusions in pavement and baskets, for example.
Custom tile patterns or mosaics can be an exciting (and expensive) addition to a design. Tiling a floor or combining polygons to create a tessellation requires that polygons be arranged in a certain way. Some tiling uses only one shape while other designs use more than one shape. The success of the pattern depends on whether the shapes line up without gaps or overlaps. This requires careful planning.
Tilers and artists apply their knowledge of the measures of angles in a polygon when designing patterns. This helps them choose the correct shapes and visualize the final design.
Use the Interior Angles of Polygons applet to help Anita create tessellations. You may be required to submit a username and a password. You can obtain these from your teacher, if necessary. Select “Interior Angles of Polygons.” Start with the “Introduction” section, and then work your way through “Concept Development” section to the “Summary” section. In this applet you will learn how to find the measure of an interior angle in a regular polygon and determine the sum of the interior angles in a regular polygon.
1.2. Discover 2
Module 2: Logic and Geometry
Try This 1
- Based on your findings from the Interior Angles of Polygons applet, make a conjecture about the relationship between the sum of the measures of the interior angles of a polygon, S, and the number of sides of the polygon, n.
- Use your conjecture from question 1 to predict the sum of the measures of the interior angles of a tridecagon (i.e., 13 sides). Verify your prediction using triangles.
Self-Check 1
Complete “Check Your Understanding” question 3 on page 99 of your textbook. Answer

© JonRiver/20863436/Fotolia
An understanding of the properties of angles of polygons is also helpful when creating puzzles such as tangrams. Invented in China between 1796 and 1802, a tangram is a seven-piece puzzle. The objective of the puzzle is to create a specific shape using all seven pieces provided without allowing any of the pieces to overlap.
Did You Know?

© Xuejun li/19276089/Fotolia
Tangrams started the world’s first puzzle craze almost 200 years ago. Napoleon Bonaparte, Lewis Carroll, Edgar Allan Poe, Hans Christian Anderson, and Michael Faraday are just some of the international celebrities who amused themselves with the tangram. Want to try out a tangram? Tangrams are available online or as an app for your favourite handheld device. A search of “tangram” or “tangram games” using an Internet search engine will provide a variety of selections.
— Adapted from Erik D. Demaine. A Lifetime of Puzzles. (London: AK Peters, 2008), p.59.
exterior angle of a polygon: an angle at a vertex of the polygon, on the outside of the polygon, formed by one side and the extension of an adjacent side
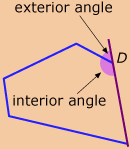
Interior angles are not the only angles that need to be considered when arranging polygons in a tile design or to solve a puzzle. To ensure that different shapes and sizes of tiles align as planned, an understanding of the exterior angles of a polygon is also required.
An exterior angle of a polygon is an angle formed by a side and an extension of an adjacent side. In Lesson 9 you learned that exterior angles and their adjacent interior angles are supplementary. The angles lie on a straight line, so their sum is 180°. You also showed that the measure of an exterior angle of a triangle is equal to the sum of the measures of the non-adjacent interior angles.
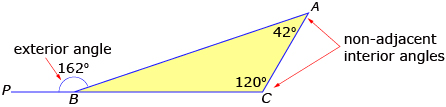
sum of exterior angle = sum of measures of the non-adjacent interior angles
162° = 42° + 120°
You have looked at how the number of sides in a polygon is related to the sum of its interior angles. Now you will look at how the number of sides in a polygon is related to the sum of its exterior angles.
1.3. Discover 3
Module 2: Logic and Geometry
Try This 2
Use the applet Exterior Angles of Polygons to investigate the measure of the exterior angles of polygons. The applet lets you experiment with three-, four-, and five-sided polygons. Restrict the shape of the polygons you create to convex polygons. Based on the evidence you gather, you will make conjectures about the measure of exterior angles of polygons.
convex polygon: a polygon in which all interior angles measure less than 180°
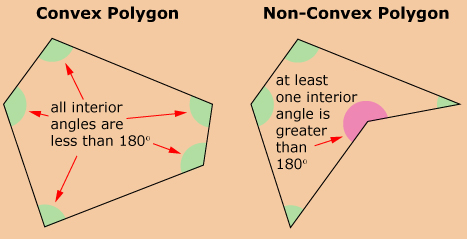
- Make a conjecture about the sum of the measures of the exterior angles of any triangle.
- Make a conjecture about the sum of the measures of the exterior angles of any convex quadrilateral.
- Make a conjecture about the sum of the measures of the exterior angles of any convex pentagon.
- Make a conjecture about the sum of the measures of the exterior angles of any convex polygon.
Share 1
Discuss your conjecture for the sum of the measures of the exterior angles of any convex polygon with another student or partner. In your discussion, consider the following questions:
- How do your conjectures about the sum of the measure of the exterior angles of any convex polygon compare?
- How are they the same?
- How are they different?
1.4. Explore
Module 2: Logic and Geometry
Explore
![]()
You proved in a previous lesson that the sum of the interior angles of any triangle is 180°.
In Discover you determined the sum of the interior angles of quadrilaterals, pentagons, and hexagons by seeing how many triangles could be drawn in each type of polygon. The sum of the measures of the interior angles of a polygon will equal the sum of the measures of the interior angles of the triangles it contains when one vertex is joined to all of the other vertices.
For example, two triangles can be drawn within a rectangle, so the sum of the interior angles in a rectangle is 2(180°) or 360°.
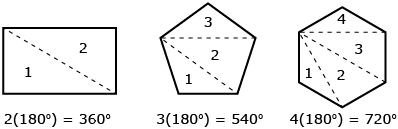
The number of triangles that can be drawn within each type of polygon by connecting one vertex to all of the other vertices is two less than the number of sides in the polygon, or n – 2. Using inductive reasoning, you developed a conjecture about the relationship between the number of sides in a polygon and the sum of the interior angles in a polygon.
 , is S
, is SiStockphoto/Thinkstock
Read “Example 1: Reasoning about the sum of the interior angles of a polygon” on page 96 of your textbook to see how deductive reasoning can be used to prove that the sum of the measures of the interior angles of a convex polygon can be expressed as S(n) = 180°(n − 2).
Self-Check 2
Complete “Your Turn” on page 96 of your textbook. Answer
Polygons are also used in many structures in nature. For instance, honeybees store their honey in honeycombs shaped like regular hexagons. Honeycombs are just one example of tessellations that can be found in nature. Recall that tessellations are arrangements of figures on a plane that completely cover a surface without gaps or overlapping.
Amaya is helping her younger brother with his science homework where he is learning about honeybees. Amaya wonders why honeycombs are shaped like hexagons. What makes the six-sided structure work better than another polygon like a pentagon? Would a pentagon even be able to tessellate? She decides to compare the angles in a hexagon and a pentagon to help answer her questions.
Watch the animation Honeycombs to see Amaya’s comparison of pentagons and hexagons.
Amaya was able to apply her knowledge of angles in polygons to help her understand a design in nature. Now it is your turn.
1.5. Explore 2
Module 2: Logic and Geometry
Self-Check 3
Complete “Practising” questions 6, 7, 11, and 13 on pages 100 and 101 of your textbook. (Note: For question 6, a loonie has 11 sides). Answer
Polygons are used in many different designs, both human-made and in nature. They can be arranged to create tessellations or other repeating patterns in custom floor tile designs, puzzles, and art, or polygons can be used as sweet storage for insects.

Hemera/Thinkstock
Planning the layout of the design is very important, especially with a complex pattern. Mistakes can be costly, time consuming, and, in nature, maybe even fatal. Amaya looked at a tessellation that involved only one type of polygon. Tessellations can be created that use more than one type of polygon in their design.
Read “Example 3: Visualizing tessellations” on page 98 of your textbook. How is an understanding of angles in polygons used to solve the problem?
Self-Check 4
Complete “Your Turn” on page 98 of your textbook. Answer
Enrico is a structural engineer who is building a house that incorporates unique designs. He really likes the idea of putting a pentagonal door in his house. As a structural engineer, however, he realizes that he will need to add two supports to the pentagon so the door does not collapse.
Did You Know?
Richard Buckminster Fuller (1895–1983), aka “Bucky,” was an American architect and inventor fascinated by nature’s principles of design. He developed the geodesic dome design. His design has been used all over the world including the Montreal Biosphere for Expo 1967.
The influence of his design can also be seen in the official design for the 1970 World Cup’s soccer ball. Fuller even has a carbon molecule named after him! In 1985, scientists discovered a molecule made up of 60 carbon atoms (C60) that were arranged in a structure similar to Fuller’s geodesic dome. This earned the molecules the names of fullerenes and buckyballs.

iStockphoto/Thinkstock

© lculig/27958779/Fotolia
He makes a quick sketch of his door design.

To create an accurate design drawing for his contractor, he needs to determine all of the angles. He knows how to find the interior angles of the pentagon as shown.

Enrico does not know the measures of the angles formed by the two supports in the door. Watch the animation Door Design to see how Enrico determines one of these missing angle measurements.
1.6. Explore 3
Module 2: Logic and Geometry
Try This 3
You will submit your answers for Try This 3 to your teacher for grading.
You can use the Lesson 11 Assignment that you saved to your course folder to complete Try This 3.
- Finish the calculation that Enrico started in the Door Design animation. Determine the measures of ∠DAO and ∠MAO in Enrico’s calculation. (5 marks)


EA = ME (given)
VMAE is isosceles.
∠MAE = ∠AME

∴ ∠MAE = 36 and ∠AME = 36
- How could congruent triangles be used to solve Enrico’s calculation? (5 marks)
Self-Check 5
This is the last lesson in this module. As you have been progressing through each lesson, you have added to your Glossary Terms document and your notes organizer. At this point, you may find it helpful to refer to the “Mid-Chapter Review” on pages 34 and 84 of the textbook and the “Chapter Review” on pages 59 and 60 and pages 117 and 118 of the textbook.
The “Frequently Asked Questions” sections provide an overview of some of the concepts covered in this module. It would be useful to review these concepts as you will be incorporating them into your project in the next section.
1.7. Connect
Module 2: Logic and Geometry
Connect
Project Connection

iStockphoto/Thinkstock
Throughout this module, you have used reasoning to solve problems relating to games, puzzles, patterns, and designs containing parallel lines and polygons. You used reasoning to identify different strategies, determine missing measurements, and verify given information.
You are now ready to complete the project for this module. Open the Module 2 Project and start designing!
Going Beyond
Assume you have an unlimited number of squares and equilateral triangles all with the same side length available to you. In this problem, you want to build larger convex polygons using the squares and triangles you have available. Recall that in convex polygons, each interior angle measures less than 180°.

You can think about it like this:
- If you can put an elastic band around the polygon and there are no empty spaces, you have built a convex polygon.
- If you have empty spaces when you put an elastic band around the polygon, you have built a non-convex polygon, which is not allowed.

Use the Building Polygons applet to build convex polygons with 7, 8, 9, 10, and 11 sides. Alternatively, you can cut equilateral triangles and squares with the same side length out of cardboard or paper. Use the applet or your paper triangles and squares to answer the following questions.
- Can you build convex polygons with more than 11 sides?
- What is the maximum number of sides that a convex polygon formed by equilateral triangles and squares can have? What is the measure of each interior angle in this polygon?
1.8. Lesson 11 Summary
Module 2: Logic and Geometry
Lesson 11 Summary

© David H. Seymour/9669715/Fotolia
Polygons can be found in building structures, floor tiles, pavement, art motifs, quilts, games, and puzzles. Designers, artists, puzzle makers, and architects have for centuries used their understanding of the angles of polygons to create successful designs. Their knowledge of the measures of angles in a polygon is applied to ensure that the shapes are arranged correctly. This helps them choose the correct shapes and visualize the final design.
An understanding of the angles of polygons is an important part of ensuring that the design works. For example, a master tiler can use his or her understanding of the angles in polygons to choose tiles and then arrange them to produce visually stimulating, complex patterns. A puzzle maker can use seven different polygons to create many different tangrams. In this lesson you used your understanding of the properties of angles and polygons to solve a variety of layout and design problems.

© JonRiver/20863431/Fotolia
You used your knowledge of the sum of the measures of the angles in a triangle to determine a formula for the sum of the measures of the angles in any convex polygon. The sum of the measures of the interior angles in a polygon was used to determine the measure of an interior angle in any regular polygon. You then applied your knowledge of exterior angles to prove that the sum of the measures of the exterior angle of any convex polygon is 360°.
In the module project you applied the concepts you learned in this module to design and then analyze a pattern or game.
You have used reasoning to solve a wide variety of problems. Refer to the Module 2 Summary for an overview of concepts you investigated in this module.