Lesson 1

Site:	MoodleHUB.ca 🍁
Course:	Math 20-2 SS
Book:	Lesson 1

Printed by:	Guest user
Date:	Saturday, 6 September 2025, 2:39 AM

Description

Created by IMSreader

1. Lesson 1

1. Lesson 1

Mathematics 20-2 M3 Lesson 1

Module 3: Quadratics

Lesson 1: Investigating Quadratic Relations

Focus

Relations can be used to describe many different real-world scenarios. For example, Mathematics 10C demonstrated how linear relations can be used to describe the speed of a car. The speed of a car can be modelled by a linear relation of the form y = mx + b.

Clockwise from left are three photos of the following: a teenage male performing a jump on his skateboard at a skateboard park; a satellite receiver antenna; a suspension bridge.

skateboard: iStockphoto/Thinkstock; dish: iStockphoto/Thinkstock; bridge: George Doyle/Stockbyte/Thinkstock

quadratic relation: a relation that can be written in standard form (y = ax2 + bx + c, where a ≠ 0); for example, 5x2 + 3x − 8

— Adapted from:
CANAVAN-MCGRATH ET AL.
Principles of Mathematics 11,
© 2012 Nelson Education Limited. p. 322.
Reproduced by permission.

Quadratic relations are another type of relation that can be used to model certain scenarios. For example, quadratic relations can be used to predict and graph the path of a skateboard in a jump. How high will the skateboard go? How far will it go? How long will it be in the air? The same is true for a thrown football, a flying hockey puck, or any projectile. Quadratic relations define the shape of satellite receivers, suspension bridge cables, and parabolic microphones.

Using quadratic relations will enable you to analyze a host of commercial and other real-world situations. Quadratic relations are useful for understanding many concepts in science, technology, business, or other fields.

Lesson Questions

This lesson will help you answer the following inquiry questions:

How do you recognize a quadratic function?
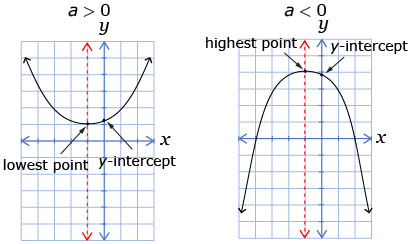
How do the values of a, b, and c in the standard form, y = ax2 + bx + c, affect the shape and location of the graph?

Assessment

Lesson 1 Assignment

All assessment items you encounter need to be placed in your course folder.

Save a copy of the Lesson 1 Assignment to your course folder. You will receive more information about how to complete the assignment later in this lesson.

Materials and Equipment

graph paper

You may find it helpful to use 1-cm Grid Paper.

1.1. Launch

Mathematics 20-2 M3 Lesson 1

Module 3: Quadratics

Launch

This section presents questions to help you determine if you have the skills and knowledge to complete this lesson successfully. Before beginning this lesson, you should be able to

fill in a table of values for relations
draw a graph using the table of values
identify whether or not a relation is a function

1.2. Are You Ready?

Mathematics 20-2 M3 Lesson 1

Module 3: Quadratics

Are You Ready?

Complete the following data table for the relation y = 2x + 4.

x	0	1	2	3	−1	−2	0.5
y

Answer

Draw a graph from the table of values from part a. Join the data points in a smooth curve. If you do not have graph paper of your own, you can use 1-cm Grid Paper. Answer

Complete the following data table for the quadratic relation y = x2 + 2.

x	0	1	2	3	−1	−2	0.5
y

Answer

Draw a graph from the table of values. Join the data points in a smooth curve. Answer

Complete the following data table for the quadratic relation y = −5(x − 1)2 + 5.

x	0	1	2	0.5	1.5
y

Answer

Draw a graph from the table of values. Join the data points in a smooth curve. Answer

This chart shows how much water vapour (in grams) a kilogram of air can hold at different temperatures.

Temperature (°C)	Water Vapour (g/kg of air)
−40	0.1
−35	0.2
−30	0.3
−25	0.51
−20	0.75
−10	1.8
0	3.8
5	5
10	7.8
15	10
20	15
25	20
30	27.7
35	35
40	49.8

What is the domain of the relation? Answer
What is the range of the relation? Answer
Make a graph of the relation. Answer

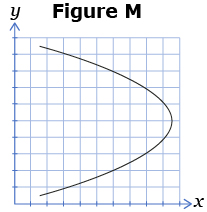
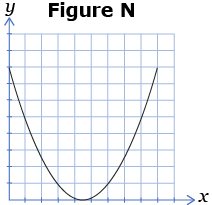
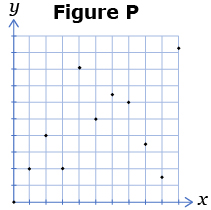
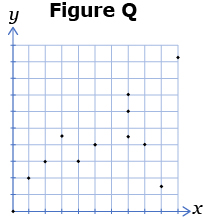
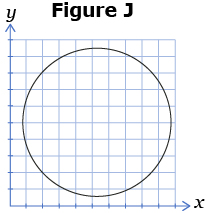
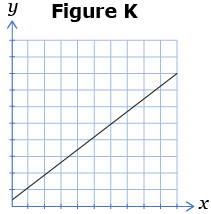
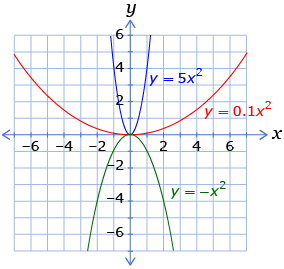
For each set of graphs, state which graph is a function and which graph is not a function. Explain how you know.
1. Answer
2. Answer
3. Answer
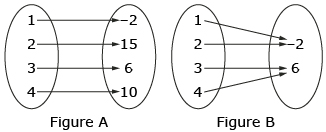
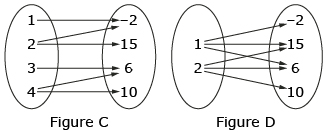
For each of the following figures, tell which figures are functions and which are not. Give a reason for your answer.

Answer
For each of the following ordered pairs, tell which sets are functions and which are not. Give a reason for your answer.

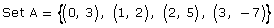
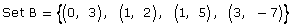
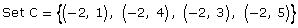
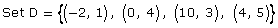
Answer

If you successfully completed the Are You Ready? questions, move on to the Discover section of the lesson.

If you experienced difficulties with the questions, use the resources in the Refresher section to review the concepts before continuing through the lesson.

1.3. Refresher

Mathematics 20-2 M3 Lesson 1

Module 3: Quadratics

Refresher

Go to Graph and watch the animation under the “Example (Mathematics)” heading to see how a table of values is used to graph a given equation. Continue to click “Play” after each step is revealed.

For information on determining the domain and range of a function, watch the “Domain and Range 1” video from the Khan Academy.

Khan Academy CC BY-NC-SA 3.0

Use the applet “Introduction to Functions” to determine whether a relation is a function. Make sure that “Show mapping diagram,” “Show ordered pairs,” and “Show graph” are selected. Follow the directions in the applet to create a relation. Select the “Show function test” boxes in each section to see whether or not the relation is a function. Use the Assessment Questions to verify that you are comfortable identifying whether a relation is a function or not.

Screenshot reprinted with permission of ExploreLearning.

Go back to the Are You Ready? section, and try the questions again. If you are still having difficulty, contact your teacher.

1.4. Discover

Mathematics 20-2 M3 Lesson 1

Module 3: Quadratics

Discover

Did You Know?

A quad is a four-wheel, all-terrain vehicle used for exploring the outdoors and having fun. Quad means “four.” But a quadratic relation has a variable taken only to the second power or, in other words, squared. The simplest example of a quadratic function is y = x2 or, as it is sometimes written, f(x) = x2. Where does the four come in?

This shows a photo of a quad jumping into the air.

iStockphoto/Thinkstock

The name came from having to find the area of the regular quadrilateral (four-sided figure) called a square. To determine the area of the square, you square the length of a side (s2) or multiply the length by itself (s × s).

Relations are rules that connect one value to another. Relations can be described as ordered pairs in which the first value is the input and the second value is the output. They can also be described in a table of values or using graphs.

Many different situations can be modelled by relations. For example, the linear relation y = 3.5x could be used to model the movement of a quad travelling at a constant speed of 3.5 m/s over a given period of time.

Time (s)	0	10	20	30	40	50	60
Distance (m)	0	35	70	105	140	175	210

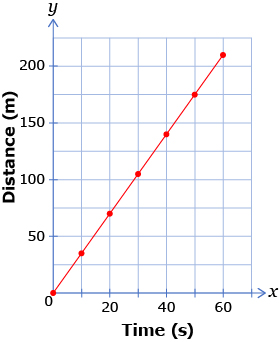
This is a distance time graph for a quad that is travelling at a constant speed of 3.5 m/s for 60 seconds.

Likewise, the path of the quad in a jump can be modelled by a quadratic relation. For example, the quadratic relation y = −5x2 + 10x describes the path of a quad during a jump where the variable y represents the height of the quad above the ground and the variable x represents time.

x	0	0.5	1	1.5	2
y	0	3.75	5	3.75	0

This is a graph shaped like a parabola that goes through (0, 0), (0.5, 3.75), (1, 5), (1.5, 3.75), and (2, 0).

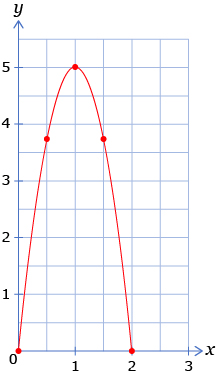
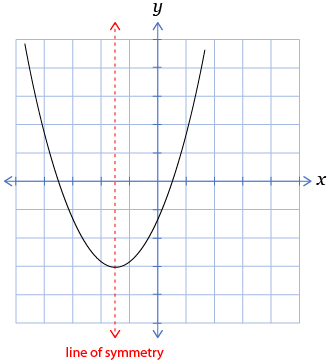
parabola: the curve-shaped graph of a quadratic relation

Notice that the graph of a linear relation is a straight line, whereas the shape of the graph of a quadratic relation is a parabola. All quadratic relations have a variable raised to the second power. Thus, all quadratic relations have a degree of 2.

For example, only one of the following functions is a quadratic function. Only one function has 2 as the highest power of the variable. If there is an exponent higher than 2 in the function, it is not a quadratic function.

f(x) = 2x + 5	This is a linear function—can be written as y = mx + b.
y = −0.2x + 5x + 4	This is a linear function—can be written as y = mx + b.
f(x) = 3x3 + 5x2 + 2x + 9	The highest power is 3, so this is not a quadratic function.
y = 3x2 + 6	This is a quadratic function. (2 is the highest power of the variable.)

Watch the video Exploring Parabolas and Polynomial Equations. Click the “Interactive” button to see other examples of quadratic relations that are used to study the flight path of objects.

1.5. Discover 2

Mathematics 20-2 M3 Lesson 1

Module 3: Quadratics

function: a relation where each input value has only one output value

A function is a relation where each input value corresponds to only one output value. There are several strategies you can use to determine whether a relation is a function. For instance, you can look at the ordered pairs to see if there is exactly one output value for each input value or you can perform a vertical line test on the graph of the relation. Recall that a graph represents a function if a vertical line cuts the graph only once.

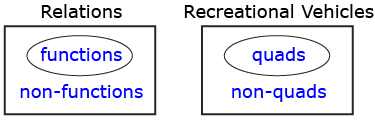
Functions are to relations what quads are to all recreational vehicles. In other words, functions are a subset or special type of relation.

A graphic shows two labelled boxes: one box is titled Relations and is made up of functions and non-functions. The other box is titled Recreational Vehicles and is comprised of quads and non-quads.

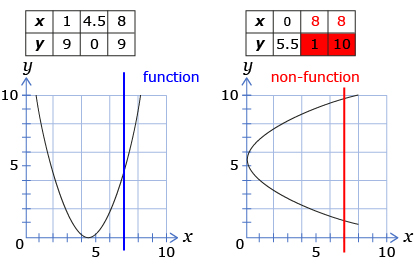
In the following examples, the relationship on the left is a function, whereas the relationship on the right is not. In the latter case, the vertical line crosses the parabola more than once showing that there is more than one output (y) value for some of the input (x) values.

The left graph shows a parabola opening upward and a vertical line that passes through exactly one point on the parabola. The right graph shows a parabola opening to the right and a vertical line passing through two points on the parabola.

If you do not remember how to determine whether or not a relation is a function, go to the Refresher section of this lesson and watch Introduction to Functions. It is important that you are comfortable determining whether or not a relation is a function when you are given ordered pairs or a graph of the relation.

Share 1

With an appropriate partner, compare quadratic and linear relationships. (How are they the same? How are they different?)

In your discussion, consider the following:

List real-life examples that are described by linear or quadratic relationships.
Describe a linear relationship.
Describe a quadratic relationship.
Describe the graphs of these relationships.
Explain how you can tell whether a graph represents a function or a non-function.
Describe patterns created by linear relationships.
Explain how these differ from patterns created by quadratic relationships.

1.6. Discover 3

Mathematics 20-2 M3 Lesson 1

Module 3: Quadratics

Did You Know?

This photo shows a car headlight.

Jupiterimages/Photos.com/

Thinkstock

The shape of the reflector inside flashlights and automobile headlamps is a parabola. This shape, formed by a quadratic function, reflects the light out in a concentrated forward beam instead of just a scattered pattern.

standard form of a quadratic function: a quadratic function written in the form y = ax2 + bx + c, where a ≠ 0

A quadratic function can be written in the form y = ax2 + bx + c. This is known as the standard form of a quadratic function.

What information does the standard form of a quadratic function tell you about the shape of the graph? How do the coefficients (a and b) and the constant (c) relate to the graph of a quadratic function?

Try This 1

Use Quadratic Functions to see what happens to the graph as you change the values of a, b, and c.

Screenshot reprinted with permission of ExploreLearning.

Once you have tried different combinations of values for the coefficients and constant, use the following questions to guide your investigation.

Begin by exploring the effect of different coefficient values on linear functions. Set the value of a to zero.
1. What type of function do you have? Answer
2. With a set to zero, change the value of b. How does this affect the graph of the linear function? Be sure to try both positive and negative values for b. Answer
3. With a set to zero, change the value of c. How does this affect the graph of the linear function? Make sure you try both positive and negative values for c. Answer

Now explore the effect of different coefficient values on quadratic functions. Set the value of b and c to zero or leave at a constant value—that is, don’t change b and c. Change the value of a. What effect does changing the value of a have on the graph of a quadratic function? Try both positive and negative values for a. Remember that a ≠ 0 or you will have a linear function. Answer

Set the value of c to zero. Set the value of a to 2. Change the value of b. Now set the value of a to −2 and repeat.
1. What effect does changing the value of b have on the graph of a quadratic function when a is positive? Answer
2. What effect does changing the value of b have on the graph of a quadratic function when a is negative? Answer
3. What effect does changing the value of b have on the location of the parabola’s line of symmetry? Answer
  
  line of symmetry: a line about which a figure is symmetrical
  
  If a figure can be folded such that the two parts exactly match, the fold line would be a line of symmetry.

Leave the value of a and b constant. Remember that a ≠ 0 or you will not have a quadratic relation. Change the value of c.
1. What effect does changing the value of c have on the graph of a quadratic function? Answer
2. What part of the graph can be determined by c? Answer

Leave the value of c constant. Change the values of a and b. What effect does this have on the y-intercept? Answer

1.7. Explore

Mathematics 20-2 M3 Lesson 1

Module 3: Quadratics

Explore

This shows a parabolic grid with Earth in the background.

Comstock/Thinkstock

The shape of the graph of a quadratic relation is called a parabola. In the photo, the thickest blue line could also be described as having a parabolic shape. Can you see the similarity between it and the graphs of the quadratic relations you have observed so far in this lesson?

In Try This 1 you discovered how changing the coefficients and constant in a quadratic function written in standard form (y = ax2 + bx + c) can affect the graph of the function. You might have noticed the connection between a and the parabola’s direction:

When a is positive, the parabolic graph open upwards.

When a is negative, the graph will open downwards.

The image on the left shows a parabola opening upwards when a is greater than zero. The lowest point on the parabola is indicated as well as the y-intercept. The image on the right shows a parabola that opens downwards when a is less than zero. The highest point on the parabola is indicated as well as the y-intercept.

Did you notice how changing the value of b changes the location of the parabola’s line of symmetry and that the highest or lowest point on the parabola lies on the vertical line of symmetry? When you left a and b constant and changed the value of c, did you determine that c is actually the value of the parabola’s y-intercept?

You also might have noticed the connection between the value of a and the shape of the graph, specifically the steepness of the opening of the parabola. Changing the value of only a (i.e., b and c are constant) changes the shape of the parabola; however, when you change the value of only b or only c, the shape of the parabola stays the same. Changing only b or only c translates the parabola horizontally or vertically, but the shape of the parabola remains the same.

1.8. Explore 2

Mathematics 20-2 M3 Lesson 1

Module 3: Quadratics

Use Try This 2 to further investigate how changing the value of a affects the steepness of the opening of the parabola when the value of b and c remains constant.

Try This 2

The Quadratic Interactive shows several graphs of quadratic functions. To the right of the graphs, you will see a slider that can be used to change the value of a.

Starting with slider a at zero, move the slider up until the black graph is hidden by the first light blue curve. Record the value of a. Continue to move the slider up, and record each value of a as the black graph is hidden by each coloured graph. Move the slider back to zero, and repeat by moving the slider downwards.

You might use a chart like the following to save your work.

Graphs Above the x-axis
Colour	light blue	purple	red	yellow	green
a-value
Graphs Below the x-axis
Colour	light blue	purple	red	yellow	green
a-value

Use your observations to answer the following questions.
1. How does the width of the graph change as the value of a changes when compared to y = x2? Describe the patterns you saw.
1. Identify two graphs that are identical reflections of each other (i.e., across the x-axis). Explain your choice.

1.9. Explore 3

Mathematics 20-2 M3 Lesson 1

Module 3: Quadratics

Self-Check 2

Match each graph with its correct function.
1. y = x2
2. y = 3x2
3. y = −4x2
4. y = 0.3x2
Answers

If you feel you need a bit more practice with the concepts presented in this lesson, complete “Further Your Understanding” questions 1, 2, 4, and 5 on page 324 in your textbook. Answers

1.10. Connect

Mathematics 20-2 M3 Lesson 1

Module 3: Quadratics

Connect

Lesson Assignment

Complete the Lesson 1 Assignment that you saved to your course folder.

Project Connection

Open the Module 3 Project and read the introduction to the project activities and the information about the three teams. (In other words, read up to the Part 1 heading.) You will begin working on the project in Lesson 3.

1.11. Lesson 1 Summary

Mathematics 20-2 M3 Lesson 1

Module 3: Quadratics

Lesson 1 Summary

In this lesson you studied a specific form of the quadratic function called the standard form, y = ax2 + bx + c. A quadratic function has a variable raised to the second power or squared. If there is an exponent higher than 2 in the function, it is not a quadratic function. You learned that the rules for determining whether a given relationship is a function holds true for quadratic relations as well as linear relations. Each input value can have only one output value. Any relation is not a function if the input value has more than one output value. In terms of x and y, each x-value can have only one y-value. However, a y-value can be paired with two or more x-values. The graph of a function must be able to pass the vertical line test, where a vertical line drawn through the graph of the function will not intersect the function in more than one place at any time.

This is a grid that contains the graphs of the quadratic functions y = 5x squared, y = 0.1x squared, and y = negative x squared.

The graph of a quadratic function forms a parabolic shape and has specific characteristics. In the Discover section you were able develop rules about the effect of changing the value of the coefficients and constants in the standard form of the quadratic function, y = ax2 + bx + c. This investigation allowed you to determine the characteristics of a quadratic function written in standard form.

The value of a in the function influences the steepness of the curve of the parabola or how wide the opening of the parabola is.
- If a is positive, the graph opens upwards. As the value of a increases above zero, the curve goes from very wide to more and more narrow.
- If the value of a is negative, the curve will open downward. As the value of a decreases below zero, the downward-opening curve becomes more and more narrow.
- If the value of a is zero, the graph forms a straight line and the relationship is a linear function, not a quadratic function.
The highest or lowest point on the graph of the quadratic function lies on its vertical line of symmetry.
The location of the parabola’s line of symmetry can be changed by changing the value of b.
The value of the parabola’s y-intercept is the constant term, c.1

In the next lesson you will investigate how to identify other characteristics of graphs of quadratic functions.

Lesson 1

Description

Table of contents

1. Lesson 1

Module 3: Quadratics

Lesson 1: Investigating Quadratic Relations

Focus

Lesson Questions

Assessment

Materials and Equipment

1.1. Launch

Module 3: Quadratics

Launch

1.2. Are You Ready?

Module 3: Quadratics

Are You Ready?

1.3. Refresher

Module 3: Quadratics

Refresher

1.4. Discover

Module 3: Quadratics

Discover

1.5. Discover 2

Module 3: Quadratics

Share 1

1.6. Discover 3

Module 3: Quadratics

Try This 1

1.7. Explore

Module 3: Quadratics

Explore

1.8. Explore 2

Module 3: Quadratics

Try This 2

1.9. Explore 3

Module 3: Quadratics

Self-Check 2

1.10. Connect

Module 3: Quadratics

Connect

Lesson Assignment

Project Connection

1.11. Lesson 1 Summary

Module 3: Quadratics

Lesson 1 Summary