Lesson 1
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-2 SS |
| Book: | Lesson 1 |
| Printed by: | Guest user |
| Date: | Tuesday, 30 December 2025, 3:42 AM |
Description
Created by IMSreader
1. Lesson 1
Module 5: Radicals
Lesson 1: Mixed and Entire Numerical Radicals
Focus

ESA, NASA, and L. Calcada (ESO for STScI)
One of the exciting areas of current space research is the search for exoplanets—planets that circle a star outside our solar system. Using new sophisticated technology, scientists have discovered over 500 exoplanets. The image shows an artist’s conception of Fomalhaut b, which is an exoplanet 25 light-years away from Earth.
The animation titled “Fomalhaut Orbit Concept” is a simulation of Fomalhaut b’s path around its star. The star is the white dot, Fomalhaut b is the red dot, and the brown ring represents dust and debris. Notice that the planet moves faster when close to the star and slower when farther away.
Many of the equations describing planetary motion involve radicals. One such equation derived from Kepler’s third law is ![]() , where
, where
- T is the time required for one revolution around the star
- k is the constant for all planets orbiting a particular star
- R is the planet’s largest distance from its star
Did You Know?
Johannes Kepler was an astronomer who formulated three laws of planetary motion in the early 1600s. If you are interested in learning more about his laws, search the Internet for “Kepler’s laws.”

© Stephane Bonnel/9272855//Fotolia
Radicals also describe a host of earthly situations, such as the skidding of a car when its brakes are applied on a wet surface or the growth of a wildlife population in an animal study.
In this lesson you will refresh some of your knowledge about working with radicals and pick up skills using them. Doing so will allow you to deal with radical expressions and equations that match situations on this planet and throughout the universe.
This lesson will help you answer the following inquiry questions:
- How do you express a mixed radical with a numerical radicand as an entire radical and vice versa?
- How do you compare and order radical expressions in a given set of mixed and entire radicals?
Time
Each module is made up of lessons. Each lesson in Mathematics 20-2 is designed to be completed in approximately 80 minutes. You may find that you require more or less time to complete different lessons depending on your strengths. It is important that you progress at your own pace based on your individual learning requirements.
Assessment
- Lesson 1 Assignment
All assessment items you encounter need to be placed in your course folder. You should have already had a discussion with your teacher about which items you will be handing in for marking. For those items that you will not be handing in for marking, you should have already had a discussion with your teacher about how you can access the solutions to these questions. Make sure to follow your teacher’s instructions.
Save a copy of the Lesson 1 Assignment to your course folder.
Materials and Equipment
- calculator
1.1. Launch
Module 5: Radicals
Launch
This section presents questions to help you determine if you have the skills and knowledge to complete this lesson successfully.
1.2. Are You Ready?
Module 5: Radicals
Are You Ready?
Answer the questions and check your solutions. If you are experiencing difficulty, you may want to use the information in the Refresher section to clarify concepts before moving on to the Discover section.
1.3. Refresher
Module 5: Radicals
Refresher
Go to Square Root to see a definition of square root and to try a demonstration applet.
Complete the Are You Ready? questions again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 5: Radicals
Discover
In a previous math course, you learned that a radical expression has a radical symbol, a radicand, and an index, as shown in the following diagram.
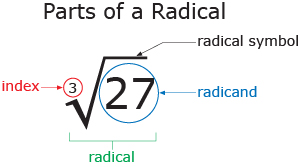
Go to Radical to see more examples of radicals, including square roots and cube roots.
This lesson involves two types of radical expressions: mixed radicals and entire radicals.
Mixed radicals have a coefficient in front of the radical symbol, and entire radicals do not have a coefficient. Here are some examples:
Mixed Radicals |
Entire Radicals |
|
Note: Since the 3 in this radical is small and raised, it is an index, not a coefficient. See the left column for examples that have coefficients. |
1.5. Discover 2
Module 5: Radicals
Kenton decides to go visit his brother, Darius, and roommate, Troy, for the weekend. To pay them back for letting him stay at their place, Kenton agrees to wait for their new wall unit to be delivered for their living room and let the delivery people know where it needs to be set up.
Troy is in college and not only does he love math but he enjoys playing practical jokes on people. The directions Troy leaves state that the wall unit is ![]() m long and the dimensions of the living room are 9 ft wide by 11 ft long. Kenton needs to figure out which wall of the living room will be used to set up the wall unit.
m long and the dimensions of the living room are 9 ft wide by 11 ft long. Kenton needs to figure out which wall of the living room will be used to set up the wall unit.
Given the shape of the room and hallways, the delivery workers will have to use the front door if the wall unit will be on an 11-ft wall or the back door if the wall unit will be on a 9-ft wall.
By the end of this lesson, you’ll be able to answer this question using your knowledge of entire and mixed radicals.
Converting an entire radical into a mixed radical is the same as writing a radical in its simplest form. A simple method of doing this is to begin by determining the prime factors of the number. This can be done using a factor tree.
Look at Factor Tree to see example factor trees for the number 30. Notice how the factor tree can be created many different ways, but it always results in the same prime factors: 2, 3, and 5.
Try This 1
In this activity, you will return to Factor Tree and use the demonstration applet to rewrite radicands as products of prime factors. Scroll down the website until you come to “Demonstration Applet.”
Using the demonstration applet, you will complete the Radical Expression Chart.
For each radical expression provided in the chart, perform the following steps. The first radical expression on the chart, 18, is done as an example.
Step 1: Enter the radicand (e.g., 18) in the grey box at the top of the applet. Then press enter.
Step 2: Click on the green box that appears.
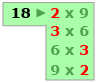
Step 3: Click on the first factored expression that appears.
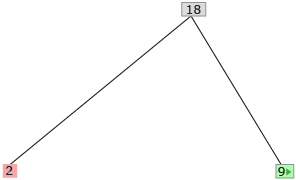
Step 4: A pink box and a green box appear. The pink box is a prime number, and the green box is not. Click on the green box again, and select the first factored expression that appears.
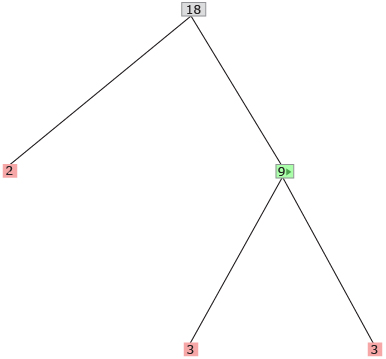
Continue this process until only pink boxes are displayed. These are the prime factors of the original number that you entered into the applet. Rewrite the radical expression with a factored radicand in the chart.
You can use prime factorization to change an entire radical into a mixed radical. Recall that perfect squares are found when multiplying a number by itself; for example, 2 × 2 = 4 and 3 × 3 = 9. It is easy to find the square root of a perfect square:
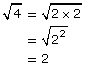 |
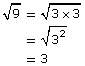 |
By writing the prime factorization as powers, the factors with even exponents can be found quickly and their square roots identified.
When dealing with cube roots, the factors that appear multiples of 3 times can be found quickly and their cube roots identified.
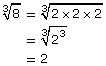 |
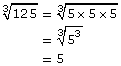 |
principal square root: the positive square root of a number
For example, the principal square root of 4 is 2.
secondary square root: the negative square root of a number
For example, the secondary square root of 4 is −2.
It is important to remember that there are principal square roots (positive) and secondary square roots (negative). Unless you are asked for both the principal and secondary square roots, the square root sign refers to the principal square root of an expression.
The next activity will help you discover what rules apply when multiplying radicals. This will help you when converting between mixed and entire radicals.
1.6. Discover 3
Module 5: Radicals
Try This 2
Use a calculator to complete the Multiplying Radicals Chart.
Remember that you may need to include brackets in your calculator to get the correct answers. For example, to enter ![]() , you will need to include brackets around the radicands. The following keystrokes will be needed for most calculators:
, you will need to include brackets around the radicands. The following keystrokes will be needed for most calculators:

You will see the following result.

Share 1
Based on your observations from the Try This 2 activity, work with a partner to create a rule that applies to the multiplication of radical expressions.
Place a copy of your rule in your course folder. You will refer to it later in the lesson.
Try This 3
The Simplifying Radicals Chart is the same as the one you completed in the Try This 1 activity, but now two columns have been added. You now have the knowledge required to fill in the final two columns.
Share 2
Compare your results from the Try This 3 activity with another student or appropriate partner. Once you have come to an agreement on the correct answers, discuss the following.
- What would be a good strategy to use in writing entire radicals as mixed radicals without using the applet?
- What can you learn from the Try This 3 activity that would help you to write mixed radicals as entire radicals?
- What would be a good strategy to use in determining whether
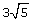 or
or 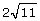 is larger?
is larger?
Summarize your discussion by creating a general procedure for writing entire radicals as mixed radicals.
Place a copy of your answers in your course folder.
Read “Example 2: Expressing a radical in simplest form” on pages 178 and 179 of your textbook. As you read, consider how the strategies used in Calvin’s solution compare to the strategies you identified in the Share 2 activity.
Did You Know?
Square Root Day occurs very rarely when both the day of the month and the month of the year are the square root of the last two digits of the year. In each century, there are nine dates when this occurs. In this century, Square Root Days are January 1, 2001 (1/1/01); February 2, 2004 (2/2/04); March 3, 2009 (3/3/09); April 4, 2016 (4/4/16); May 5, 2025 (5/5/25); June 6, 2036 (6/6/36); July 7, 2049 (7/7/49); August 8, 2064 (8/8/64); and September 9, 2081 (9/9/81).
1.7. Explore
Module 5: Radicals
Explore
If you recognize that a perfect square is a factor of your radicand, you can simply write the radicand as the product of the perfect square and another number and then simplify.
Self-Check 1
Consider the radical ![]() .
.
- Write the radicand as a product of two factors, one of which is a perfect square. Answer
- Simplify the result by evaluating the square root of the perfect square. (Hint:
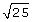 is the perfect square.) Answer
is the perfect square.) Answer
- Write the expression as a mixed radical. Answer
- Use your calculator to verify that the result is equal to
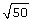 . Answer
. Answer
- What other ways could you simplify
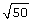 ? Answer
? Answer
Self-Check 2
Change the following entire radicals into equivalent mixed radicals using one method; then check your answers using the other method. Which method works better for you? Be sure to check your answers to ensure that you understand the solution process.
1.8. Explore 2
Module 5: Radicals
Try This 4
There may be times when you want to change a mixed radical to an entire radical. The same rules of exponents and roots apply.
For example, change the mixed radical ![]() into an entire radical.
into an entire radical.
- Write the coefficient under the radical sign with the index as its exponent. Answer
- Arrange for all factors to have an exponent of 1. Answer
- Simplify to write the expression as an entire radical. Answer
- Use your calculator to verify that the result is equal to
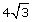 . Answer
. Answer
The same procedure is used for cube roots. For example, change the mixed radical ![]() into an entire radical.
into an entire radical.
- Write the coefficient under the radical sign with the index as its exponent. Answer
- Arrange for all factors to have an exponent of 1. Answer
- Simplify to write the expression as an entire radical. Answer
- Use your calculator to verify that the result is equal to
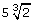 . Answer
. Answer
Example
Change ![]() to an equivalent entire radical.
to an equivalent entire radical.
Begin by expressing the coefficient as a square root because the radical is a square root.
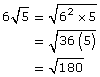
Check by computing the values for the original question and the answer using a calculator.
1.9. Explore 3
Module 5: Radicals
Self-Check 3
Change the following mixed radicals into equivalent entire radicals. Check by using a calculator to compute the numerical value of both the question and the answer. Be sure to check your answers to ensure that you understand the solution process.
Sometimes it will be necessary to compare radicals and sort them from smallest to largest or vice versa. To do this accurately, make sure all the radicals are expressed as entire radicals.
Suppose you were asked to put the following numbers in order from smallest to largest:
![]()
![]()
![]() 4
4 ![]()
Begin by expressing each of the numbers as an equivalent entire radical.
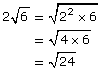
![]() is already expressed as an entire radical.
is already expressed as an entire radical.
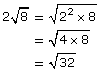
![]()
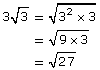
Now it is easy to order them from smallest to largest.
4 ![]()
![]()
![]()
![]()
Self-Check 4
Put the following numbers in order from smallest to largest:
![]()
![]()
![]()
![]()
![]()
If you feel you need a bit more practice converting radicals between entire and mixed forms or comparing and ordering radical expressions, complete “Check Your Understanding” question 2 and “Practising” questions 4, 11, 12, and 15 on pages 182 and 183 of your textbook.
When you finish each question, check your work using the shortened answers given on page 538 of your textbook. If you are still unclear about how to answer some questions, make sure you contact your teacher to ask about those questions and get some assistance.
If you haven’t already done so, you should update your Glossary Terms document with the following definitions from this lesson:
- mixed radical
- entire radical
- principal square root
- secondary square root
1.10. Connect
Module 5: Radicals
Connect
Lesson Assignment
Complete the Lesson 1 Assignment that you saved to your course folder.
Project Connection
The Module 5 Project uses a dot paper approach to squares and square roots. It will help in your understanding of these lessons.
Open your Module 5 Project, and complete both the Are You Ready? section and Part 1.
Save your work in your course folder, as you will need to submit it with your project at the end of Lesson 3.
Going Beyond
A potentially habitable exoplanet, Gliese 581 g, has been discovered. To learn more, go to an Internet search engine and type the keywords “NASA+Gliese 581.” This should take you to the NASA website and an item titled “NASA and NSF-Funded Research Finds First Potentially Habitable Exoplanet.”
Find out more about Fomalhaut b and other exoplanets by going to an Internet search engine and typing the keywords “NASA+Fomalhaut b.” You should find an item titled “Hubble Directly Observes a Planet Orbiting Another Star.”
What other telescopes are being used besides the Hubble? What other planets have recently been discovered?
1.11. Lesson 1 Summary
Module 5: Radicals
Lesson 1 Summary

© HOWARD/3989675/Fotolia
In this lesson you started your work with radicals. You looked at converting entire radicals to mixed radicals and mixed radicals to entire radicals. You saw that prime factorization can be a major aid in these conversions. You also saw that you can use your calculator to check your conversions. Your calculator can also be useful when you need to order radicals.
In the next lesson you will enhance your ability to work with radicals, including working with radicals that have variable radicands.