Lesson 2
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-2 SS |
| Book: | Lesson 2 |
| Printed by: | Guest user |
| Date: | Tuesday, 30 December 2025, 7:27 AM |
Description
Created by IMSreader
1. Lesson 2
Module 5: Radicals
Lesson 2: Mixed and Entire Radicals that Include Variables
Focus

Hemera/Thinkstock
When driving in a car and there’s a sign indicating a bump in the road, most people tend to slow down a bit. When the vehicle goes over the bump, the speed at which the vehicle hits the bump, as well as the springs in the car, will have an effect on how much a person moves in his or her seat.
Physicists study things that impact motion, and they have developed a formula to calculate the distance a person will be displaced by the bump and the speed at which the person returns to his or her regular position. And wouldn’t you know—it’s a radical equation. ![]()
If a vehicle hits the bump too fast, the person may lift up off of the seat. When this happens, most people aren’t thinking about the equation. The higher the bump and the faster the vehicle is travelling, the more the person will move inside the car.
In this lesson you will apply what you already know about converting between entire radicals and mixed radicals to expressions in which the radicand contains variables. You know that it’s not possible to find the square root of a negative number, so you will need to identify the values of the variables for which the radical expression is defined. Doing so will allow you to better understand and work with radical equations, such as the example of the speed bump and the many other radical expressions that you will encounter in the future.
This lesson will help you answer the following inquiry questions:
- How do you express a mixed radical that includes variables in the radicand as an entire radical?
- How do you express an entire radical with a variable coefficient as a mixed radical?
- How do you identify values of the variable for which the radical expression is defined?
Assessment
- Lesson 2 Assignment
All assessment items you encounter need to be placed in your course folder. You should have already had a discussion with your teacher about which items you will be handing in for marking. For those items that you will not be handing in for marking, you should have already had a discussion with your teacher about how you can access the solutions to these questions. Make sure to follow your teacher’s instructions.
![]() Save a copy of the Lesson 2 Assignment to your course folder.
Save a copy of the Lesson 2 Assignment to your course folder.
Materials and Equipment
- calculator
1.1. Launch
Module 5: Radicals
Launch
This section presents questions to help you determine if you have the skills and knowledge to complete this lesson successfully.
1.2. Are You Ready?
Module 5: Radicals
Are You Ready?
Answer the questions and check your solutions. If you experience difficulty, you may want to use the information in the Refresher section to clarify concepts before moving on to the Discover section.
1.3. Refresher
Module 5: Radicals
Refresher
Simplifying square roots with variables is similar to simplifying square roots with numerical radicands. First, find the prime factorization of the coefficient of the expression. Then, change the entire radical to a mixed radical by treating each variable of the expression as if it were a prime number. You will recall that perfect squares are found when multiplying a number by itself. The same is true for variables. Here are some examples:
2 × 2 = 4
3 × 3 = 9
x × x = x2
y2 × y2 = y4
It is easy to find the square root of a perfect square. Here are some examples:
![]()
![]()
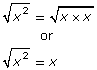
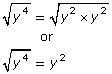
By writing the prime factorization as powers, factors with even exponents can be found quickly and their square roots identified.
Remember that there are principal square roots (positive) and secondary square roots (negative). Unless you are asked for both the principal and secondary square roots, the square root sign refers to the principal square root of an expression.
Identifying perfect cubes can also help you find cube roots:
2 × 2 × 2 = 8
3 × 3 × 3 = 27
x × x × x = x3
y2 × y2 × y2 = y8
The cube roots of these expressions are
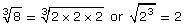
![]()
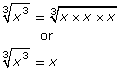
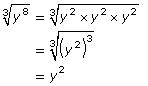
Go back to the Are You Ready? section, and try the questions again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 5: Radicals
Discover

iStockphoto/Thinkstock
You already know that you cannot take the square root of a negative number. When you find a square root, you find two numbers that multiply to equal the radicand. For example, to find the square root of 9, find a number that, when multiplied by itself, equals 9.
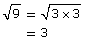
You cannot multiply a number by itself and get a negative answer.
(−3)(−3) = 9
Is it possible to take the cube root of a negative number? What about the fourth root?
Try This 1
Use your calculator to complete Decimal Approximation Chart. You are finding various roots of 2000 and −2000.
There are different ways to find roots, other than square roots, on your calculator. One way is to use a button that allows you to enter the index of a radical. This button often looks like ![]()
The other way is to use an exponent button, usually represented as “^” on calculators. Recall from Mathematics 10C that roots are equivalent to fractional exponents. To find the cube root of a number, raise it to the ![]() power. For a fourth root, raise it to the
power. For a fourth root, raise it to the ![]() power, and so on. Be sure to remember to enclose fractions in parentheses. You also need to remember to enclose negative numbers in parentheses, as shown. The keystrokes used are shown.
power, and so on. Be sure to remember to enclose fractions in parentheses. You also need to remember to enclose negative numbers in parentheses, as shown. The keystrokes used are shown.
![]()

If your calculator has an “xy” button, put in the number, press the “xy” button, and then put in the appropriate fractional exponent in brackets.
Share 1
Compare your results from Try This 1 with another student or appropriate partner. Once you have come to an agreement on the correct answers, discuss the following questions:
- When is it possible to take the root of a negative number? Describe the patterns you see.
- What rules describe the situation?
Summarize your discussion by creating a general rule about taking the root of a negative number.
![]() Place a copy of your work in your course folder.
Place a copy of your work in your course folder.
1.5. Explore
Module 5: Radicals
Explore
restrictions: a statement of the values of a variable that ensure the expression is defined
In the Discover section you learned that sometimes you can calculate the root of a negative number depending on what the index of the radical is. When you tried to calculate the square root of −2000, you got an error message. Your calculator may have even displayed a message telling you that the result is a non-real answer. When you work with radical expressions that have variables, it is important to specify restrictions on the variable. All you need to do is write a short mathematical statement that identifies the values of the variable that allow the expression to be simplified or defined.
For example, in the expression ![]() , if x is negative, then the radicand becomes negative. Since you can’t find the square root of a negative number, x cannot be negative. On the other hand, if y is negative, the radicand is still positive because any number raised to the fourth power will always be positive. (You can try it on your calculator.) So, the restrictions on the variable are that x cannot be negative and y can be any real number. To state the restrictions on the variable in the expression
, if x is negative, then the radicand becomes negative. Since you can’t find the square root of a negative number, x cannot be negative. On the other hand, if y is negative, the radicand is still positive because any number raised to the fourth power will always be positive. (You can try it on your calculator.) So, the restrictions on the variable are that x cannot be negative and y can be any real number. To state the restrictions on the variable in the expression ![]() using mathematical notation, you can simply write x ≥ 0, x ∈
using mathematical notation, you can simply write x ≥ 0, x ∈ ![]() , y ∈
, y ∈ ![]() .
.
If the index of the radical is even, then the radicand cannot be a negative number. For example, all of the following are undefined:
![]()
If the index of the radical is odd, then the radicand can be a negative number. For example, all of the following can be simplified:
![]()
![]()
![]()
Read “Example 1: Working with radicals that contain variables” on pages 204 and 205 of your textbook. You will notice that the absolute value sign, |x|, is used in the solutions. Be sure to read “Communication Tip” on page 205 where its use in this section is explained.
1.6. Explore 2
Module 5: Radicals
Self-Check 1
Complete “Check Your Understanding” question 1 on page 211 of your textbook. Answer

iStockphoto/Thinkstock
In Lesson 1 you learned two methods to convert an entire radical to a mixed radical. You can find the prime factorization or you can find the greatest perfect square factor (or greatest perfect cube when working with cube roots). It doesn’t matter if the expression is made up of numbers or variables, the procedure is the same.
You can find the greatest perfect square (or greatest perfect cube) factor of numbers in order to simplify radical expressions:
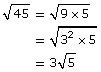
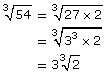
You can find the greatest perfect square (or greatest perfect cube) factor of variables in order to simplify radical expressions:
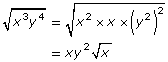
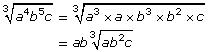
You can find the greatest perfect square (or greatest perfect cube) factor of a combination of both numbers and variables in order to simplify radical expressions:
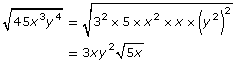
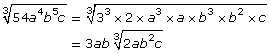
Try This 2
Convert ![]() to a mixed radical.
to a mixed radical.
- Write the radicand as a product of two factors, one of which is a perfect square. Be sure to include variables. Answer
- Simplify the result by taking the square root of the perfect square out of the radicand.
 Answer
Answer
- Use your calculator to verify that the result is equal to
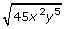 by substituting in values for x and y, such as 3 for x and 2 for y. Answer
by substituting in values for x and y, such as 3 for x and 2 for y. Answer
- What other ways could you simplify
 ? Answer
? Answer
1.7. Explore 3
Module 5: Radicals
Another way to convert to a mixed radical is to completely factor the radicand into prime factors.
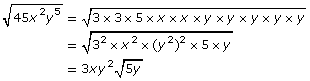
Self-Check 2
Change the following entire radicals into mixed radicals, and state any restrictions on the variables.
The radical sign represents the principal root of a number. Even though (−4)² = 16, mathematicians have agreed that the radical symbol results in a positive number, so ![]() . If the secondary root is wanted, it must be specified as
. If the secondary root is wanted, it must be specified as ![]() . If both principal and secondary roots are wanted, they should be specified as
. If both principal and secondary roots are wanted, they should be specified as ![]() .
.
The radical ![]() is only defined as a real number if x is greater than or equal to zero. In other words, it cannot be a negative number. However, the value of
is only defined as a real number if x is greater than or equal to zero. In other words, it cannot be a negative number. However, the value of ![]() is defined as a real number for all values of x because x2 will be positive whether x is positive or negative.
is defined as a real number for all values of x because x2 will be positive whether x is positive or negative.
To convert a mixed radical to an entire radical, you apply the same process whether you have variables in the expression or not.
Try This 3
Change the mixed radical ![]() into an entire radical.
into an entire radical.
- Write each term of the coefficient under the radical sign with the index as its exponent. Answer
- Arrange all numerical factors to have an exponent of 1 and find the resulting product. Answer
- Check your work. Substitute a value for the variable in the mixed radical and the entire radical, and use your calculator to verify that the results are the same. Answer
The same procedure can also be used for cube roots. Change the mixed radical ![]() into an entire radical.
into an entire radical.
1.8. Explore 4
Module 5: Radicals
Self-Check 3
Change the following mixed radicals into entire radicals, and state any restrictions on the variables. Check by using a calculator to compute the numerical value of both the question and the answer.
Did You Know?
Although radical numbers, such as the square root of 2, have been known since the time of ancient Greece, about 2600 years ago, the radical sign ![]() has only been used for about 600 years. It first appeared in print in a German algebra book by Christoff Rudolff. This book also introduced the use of + and − signs.
has only been used for about 600 years. It first appeared in print in a German algebra book by Christoff Rudolff. This book also introduced the use of + and − signs.
The term to be added from this lesson is
- restrictions
1.9. Connect
Module 5: Radicals
Connect
Lesson Assignment
![]() Complete the Lesson 2 Assignment that you saved to your course folder.
Complete the Lesson 2 Assignment that you saved to your course folder.
Project Connection
Open the Module 5 Project, and complete Part 2.
1.10. Lesson 2 Summary
Module 5: Radicals
Lesson 2 Summary
To convert entire radicals, whether or not they include variables, to mixed radicals, you can use prime factorization. Or, if the radicand has a factor that is a perfect square or a perfect cube, you can factor out the greatest perfect square or perfect cube.
 iStockphoto/Thinkstock
iStockphoto/Thinkstock
When there are variables present in a radical, you have to consider what values will ensure that the solution is a real number. When you do this, you need to state whether there are restrictions on possible values of the variable. It is important to keep in mind the index of the radical when you do this. If the index of the radical is even, then the radicand cannot be a negative number. For example, ![]() If the index of the radical is odd, then the radicand can be a negative number. For example,
If the index of the radical is odd, then the radicand can be a negative number. For example, ![]()
In the next lesson you will learn how to add and subtract radicals.