Lesson 3
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-2 SS |
| Book: | Lesson 3 |
| Printed by: | Guest user |
| Date: | Tuesday, 30 December 2025, 4:05 AM |
Description
Created by IMSreader
1. Lesson 3
Module 5: Radicals
Lesson 3: Adding and Subtracting Radicals
Focus

© Sandor Kacso/12225139/Fotolia
Knowing how to work with a radical expression and simplify it correctly is needed in all branches of science, not just physics and astronomy. For example, chemists often combine different elements and substances. They need, however, to exercise caution in their labs. If a chemical reaction occurs too quickly, it may be violently explosive. If it occurs too slowly, the substance may remain as a pollutant in the environment for decades. When substances A and B combine to produce C, a radical equation involving the rate of reaction and concentration of substances is ![]()
In this lesson you will enhance your ability to work with radicals, including adding, subtracting, and simplifying them and their components.
This lesson will help you answer the following inquiry questions:
- How do you add radical expressions?
- How do you subtract radical expressions?
Assessment
- Lesson 3 Assignment
- Module 5 Project
All assessment items you encounter need to be placed in your course folder.
Save a copy of the Lesson 3 Assignment to your course folder. You will receive more information about how to complete the assignment later in this lesson.
Materials and Equipment
- calculator
1.1. Launch
Module 5: Radicals
Launch
This section presents questions to help you determine if you have the skills and knowledge to complete this lesson successfully.
1.2. Are You Ready?
Module 5: Radicals
Are You Ready?
Answer the questions and check your solutions. If you are experiencing difficulty, you may want to use the information in the Refresher section to clarify concepts before moving on to the Discover section.
Simplify the following variable expressions by adding or subtracting. If an expression cannot be simplified, explain why not.
1.3. Refresher
Module 5: Radicals
Refresher
Visit Like Terms to find a definition of like terms and how to work with them.
Go back to the Are You Ready? section, and try the questions again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 5: Radicals
Discover
In earlier math courses, you learned that (6) + (7) = (6 + 7). Is this true for radicals? Does ![]() ?
?
Try This 1
Use a calculator to complete Adding Radicals Chart.
You will need to include brackets as you enter these calculations in your calculator. For example, to enter ![]() you will need to include brackets around the radicands. The following keystrokes will be needed for most calculators.
you will need to include brackets around the radicands. The following keystrokes will be needed for most calculators.
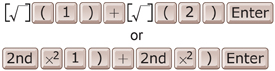

You also know from earlier math courses that 6(2) + 4(2) = (6 + 4)(2). Is this true for radicals? Does ![]() ?
?
Try This 2
Use a calculator to complete Mixed Radicals Chart. You will likely need to include brackets as you enter the expressions in your calculator.
Share 1
Based on your observations from both of the Try This activities, work with a partner to create a rule that applies to the addition of radical expressions.
![]() Place a copy of your work in your course folder.
Place a copy of your work in your course folder.
1.5. Explore
Module 5: Radicals
Explore

iStockphoto/Thinkstock
As you saw in the Discover section, adding and subtracting radicals works the same as adding and subtracting like terms. In the case of radicals, the radicands are considered the like terms. Just as you can’t always simplify a variable expression all the way down to one term, you can’t always simplify a radical expression down to one term. We have all heard the expression “you can’t add apples and oranges.” In order to add or subtract radical terms, they have to have the same radicand and index.
like terms: terms that have the same set of variable bases and corresponding exponents
For example, 6x and 13x are like terms with a variable base of x to the exponent 1. They are like terms since they have the common variable factor of x.
Did You Know?
Square roots and cube roots can be written with fractional exponents. For example,
![]()
For that reason, radical expressions can be treated just like other variables with exponents and polynomials. The rules that apply to monomial and binomial expressions also apply to radicals when adding, subtracting, multiplying, and dividing. In the same way that you can’t combine by addition
4n4 + 2n3 because they are not like terms, you can’t add 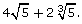 The same distributive property and multiplication properties apply to radical expressions as apply to other expressions.
The same distributive property and multiplication properties apply to radical expressions as apply to other expressions.
Selena and Josh are working together on their homework, and the assignment is to simplify some radical expressions that require adding and subtracting. They use different methods to simplify the expressions. Look at Selena’s and Josh’s Solutions to decide which method you would prefer to use when simplifying radicals.
Read “Example 3: Simplifying radical expressions” on pages 186 and 187 of your textbook. As you read, look closely at the strategies Vanessa uses to simplify the radical expressions. What is the first step that she used in both questions?
Self-Check 1
- For each of the following questions, simplify by adding or subtracting.
- Simplify the following radicals, and then combine like terms.
- Simplify radicals and combine like terms.
Answers
- Complete “Practising” question 10 on page 189 of your textbook. Answer
If you haven’t done so already, now would be a good time to update your Glossary Terms document. Remember to save your updated document to your course folder.
The term to be added for this lesson is
- like terms
1.6. Connect
Module 5: Radicals
Connect
Lesson Assignment
Complete the Lesson 3 Assignment that you saved to your course folder.
Project Connection
Go to the Module 5 Project, and complete Part 3.
Be sure to submit all components of the Module 5 Project to your teacher at this time.
1.7. Lesson 3 Summary
Module 5: Radicals

Hemera/Thinkstock
Lesson 3 Summary
Much like you can add and subtract numbers and variable expressions, you can add and subtract radicals. The key is to ensure that you are working with like terms. Once you simplify each term in the expression, you can add or subtract any terms that have the same radicand and index. If there are terms that do not have the same radicand and index, they cannot be combined. Just as you can’t always simplify a variable expression all the way down to one term, you can’t always simplify a radical expression down to one term.
In the next lesson you will learn how to multiply and divide radical expressions.