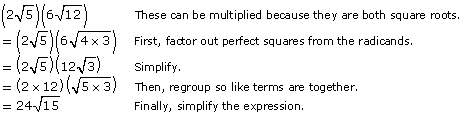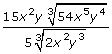Lesson 4
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-2 SS |
| Book: | Lesson 4 |
| Printed by: | Guest user |
| Date: | Tuesday, 30 December 2025, 1:47 AM |
Description
Created by IMSreader
1. Lesson 4
Module 5: Radicals
Lesson 4: Multiplying and Dividing Radicals
Focus

Digital Vision/Thinkstock
Skydivers jump out of an airplane and free fall through the air. As they fall, their speed increases until they open their parachutes. You can calculate a skydiver’s velocity during the first part of the skydiving jump by using the radical expression ![]() where
where
- d is the distance the skydiver has fallen in metres
- a is the acceleration due to gravity, which on Earth is 9.8 m/s2
- vi is the initial velocity in m/s
- vf is the final velocity in m/s at distance d
While most skydivers likely don’t calculate their velocity, it is important that the designers of parachutes have done these and other calculations so the parachute will safely return the skydivers to the ground. You don’t have to be a young physics genius to know that radical expressions are important. Knowing how to work with a radical expression and simplify it correctly is needed not just in science, but also in art, finance, human relations, political science, business, astronomy, and a host of other fields.
In this lesson you will multiply, divide, and simplify radical expressions. These are essential skills needed to deal effectively with the radical expressions and equations you will encounter in the next lessons.
This lesson will help you answer the following inquiry questions:
- How do you multiply radical expressions?
- How do you divide radical expressions?
Assessment
- Lesson 4 Assignment
All assessment items you encounter need to be placed in your course folder.
Save a copy of the Lesson 4 Assignment to your course folder. You will receive more information about how to complete the assignment later in this lesson.
Materials and Equipment
- calculator
1.1. Launch
Module 5: Radicals
Launch
This section presents questions to help you determine if you have the skills and knowledge to complete this lesson successfully. Before beginning this lesson, you should be able to
- multiply variable expressions with exponents
- divide variable expressions with exponents
1.2. Are You Ready?
Module 5: Radicals
Are You Ready?
Answer the questions and check your solutions. If you are experiencing difficulty, you may want to use the information in the Refresher section to clarify concepts before moving on to the Discover section.
Simplify each of the following expressions.
1.3. Refresher
Module 5: Radicals
Refresher
Visit Exponent to find a definition of exponents and examples.
Next, visit the Exploring Laws of Exponents—Explore It activity to review the laws for multiplying and dividing expressions involving exponents.
You can review simplifying radicals, using the Simplifying Radicals—Activity B gizmo. When you are sure you are comfortable with the skills, complete the four assessment questions at the bottom; then click on the “Check your Answers” button.
To watch a video to multiply binomials together, go to the Internet and type the keywords “Math Dude” into a search engine. These keywords should take you to the Montgomery County Public Schools website. On the right side of the website, look for the heading “Algebra 1 Unit 6.” Then choose the video titled “Multiplying Polynomials.”
Go back to the Are You Ready? section, and try the questions again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 5: Radicals
Discover
In Lesson 3 you learned that radicals cannot be added together if they have different radicands, so ![]() does not equal
does not equal ![]() (Different radicands cannot be subtracted, either; therefore,
(Different radicands cannot be subtracted, either; therefore, ![]() does not equal
does not equal ![]() ) You can, however, add two radicals together if they have the same radicand, so
) You can, however, add two radicals together if they have the same radicand, so ![]() (For subtraction, this means
(For subtraction, this means ![]() )
)
Is the same true for multiplication and division? What are the restrictions and rules that apply when multiplying and dividing radicals?
Try This 1
Use a calculator to complete the Multiplying Radicals Chart.
Remember that you may need to include brackets in your calculator to get the correct answers. To enter ![]() , for example, you will need to include brackets around the radicands. The following keystrokes will be needed for most calculators:
, for example, you will need to include brackets around the radicands. The following keystrokes will be needed for most calculators:
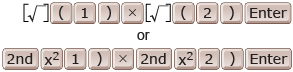

Try This 2
Use a calculator to complete Dividing Radicals Chart.
Share 1
Based on your observations from both of the Try This activities, work with a partner to create a rule that applies to the multiplication and division of radical expressions.
Place a copy of the rule you created in your course folder.
1.5. Explore
Module 5: Radicals
Explore

Digital Vision/Thinkstock
In physics, as in other sciences, calculations involving radicals are often used to explain observations and predict results, even for skydiving.
In Lesson 3 Josh used a simple method to add or subtract radicals. As long as the radicands and indices (the plural of index) were the same, he added or subtracted the coefficients but he never changed the radicands.
When multiplying and dividing radicals, you need to work with both the coefficients and the radicands. For example, when multiplying radicals, the indices must be the same. If they are the same, start by multiplying the coefficients and then multiply the radicands. You cannot simplify an expression by multiplying or dividing a square root by a cube root.
![]()
In previous math courses, you learned a number of rules for multiplying and dividing monomials, binomials, and polynomials. Those same rules apply to radicals, but remember that radicals must have the same indices to be multiplied or divided.
1.6. Explore 2
Module 5: Radicals
Multiplication of Radicals
There are two general rules when multiplying radicals:
Multiplying Entire Radicals
Read the following or go to Multiplying Entire Radicals.
You can simplify the following expression:
![]()


Can you see an alternative solution to this problem? You could have simplified one of the original terms before multiplying.

1.8. Explore 4
Module 5: Radicals
Multiplying More Complex Radical Expressions
Read the following or go to Multiplying Complex Radicals.
So far, all of the expressions have been monomials. The same rule applies to binomials.
You can use these rules to simplify the following:
![]()

This process can be used to simplify another binomial product. Read the following or go to Multiplying Binomial Radicals.
![]()
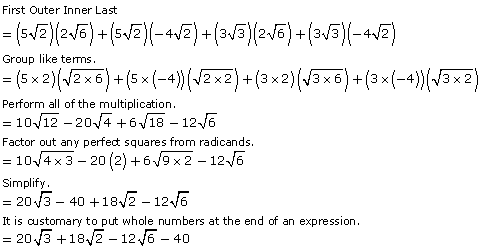
Did You Know?
A special case of multiplication that you may recall from your Grade 10 math course is the multiplication of binomial conjugates. Binomial conjugates are two binomials that are otherwise identical; but one is the addition of the terms, and the other is the subtraction of the terms. When these are multiplied together, there is a difference of squares.
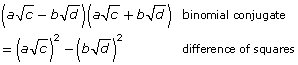
1.9. Explore 5
Module 5: Radicals
Self-Check 1
Simplify the following radicals by multiplication. For questions 2, 3, and 4, state any restrictions on the variables. Be sure to look at the original expression when stating restrictions on variables.
Dividing Radicals
There are two general rules when dividing radicals:
Dividing Entire Radicals
Read the following or go to Dividing Entire Radicals.
You can simplify the following expression:
![]()

1.10. Explore 6
Module 5: Radicals
Dividing Mixed Radicals
Read the following or go to Dividing Mixed Radicals.
You can simplify the following expression:
![]()

Then read the following or go to Dividing Complex Radicals.
Simplify the following complex radical:
![]()

Did You Know?
Radicals can be simplified by multiplying and dividing only if they have the same index. If they do, you can multiply the coefficients and multiply the radicands, 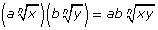 , or divide the coefficients and divide the radicands,
, or divide the coefficients and divide the radicands, 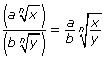 .
.
In the case of division, n must be a natural number; b and y cannot equal zero; and a, b, x, and y must be real numbers. If n is even, x ≥ 0 and y > 0.
1.11. Explore 7
Module 5: Radicals
Self-Check 2
Simplify the following radicals, and state any restrictions on the variables.
If you need extra practice dividing radicals, work through the Simplifying Radicals—Activity A gizmo. Skip all the questions that say “Simplify by rationalizing the denominator” by clicking on the “New” button to go to the next question. When you are sure you are comfortable with the skills, complete Assessment Questions 1, 2, 4, and 5 at the bottom. Then click on the “Check Your Answers” button.
Review the rules for working with radicals by looking at “Key Idea” and “Need to Know” on page 197 of your textbook. The last point will be used in the next lesson, so you can put it on hold until then.
Also, review the rules for working with radicals containing variables by looking at “Key Ideas” and “Need to Know” on page 211 of your textbook.
1.12. Connect
Module 5: Radicals
Connect
Lesson Assignment
Complete the Lesson 4 Assignment that you saved to your course folder.
Going Beyond
In the Focus section for this lesson, you were given an equation relating the velocity of a skydiver to the distance he or she has fallen before opening the parachute.
Use the equation ![]() where
where
- d is the distance the skydiver has fallen in metres
- a is the acceleration due to gravity, which on Earth is 9.8 m/s2
- vi is the initial velocity in m/s
- vf is the final velocity in m/s at distance d
Alfredo had an initial velocity of 0 and has fallen 200 m. How fast is Alfredo falling? Make sure to round your answer to the nearest tenth of a metre per second. Answer
1.13. Lesson 4 Summary
Module 5: Radicals
Lesson 4 Summary

Hemera/Thinkstock
The same rules used for multiplying and dividing monomials, binomials, and polynomials in previous math courses also apply to radicals.
When multiplying and dividing radicals, you need to work with both the coefficients and the radicands. The key to multiplying and dividing radicals is to be sure that they have the same index. Just as you can’t mix apples and oranges, you can’t multiply or divide radicals that have different indices.
When multiplying radicals, first multiply the coefficients, and then multiply the radicands. When dividing radicals, first divide the coefficients, and then divide the radicands. In both cases, you must always simplify your answer so that the radical is in lowest terms.
You also looked at restrictions on the variables in radicals. If the index is an even number, the radicands cannot have a negative number. If the index is an odd number, the radicand could be negative or positive, so there are no restrictions on the variable. The exception to this is when you have a variable in the denominator because division by zero is undefined. If there is a variable in the denominator, then you must state the restriction that the variable cannot equal zero.
In the next lesson you will simplify fractional radicals further by learning to write them without a radical in the denominator.