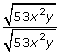Lesson 5
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-2 SS |
| Book: | Lesson 5 |
| Printed by: | Guest user |
| Date: | Tuesday, 30 December 2025, 4:04 AM |
Description
Created by IMSreader
1. Lesson 5
Module 5: Radicals
Lesson 5: Rationalizing Radical Expressions
Focus

diver on cliff: Medioimages/Photodisc/Thinkstock; diver in air: Brand X Pictures/Thinkstock
La Quebrada Cliff Divers at Acapulco, Mexico, are trained divers who entertain tourists with spectacular dives.
Trained professional cliff divers or Clavadistas at Acapulco, Mexico, leap out from the cliff face and plunge 35 m into a shallow gorge below. That is comparable to diving off a 12-storey building. In the gorge, the water depth varies from 2 m to 5 m, depending on the wave action. Timing a jump is essential in order to be sure that the water is deep enough that the diver does not hit the rocky ocean floor.
In order to be as safe as possible when cliff jumping, divers make sure ahead of time that the water is deep enough and there are no hidden ledges or rocks in the water below them. A formula to calculate the time it takes for the diver to hit the water is
![]()
In this lesson you will learn to simplify fractional radicals by writing them without a radical in the denominator.
This lesson will help you answer the following inquiry questions:
- How do you simplify a fractional radical by rationalizing the denominator?
- How do you explain, using examples, the rules for writing positive and negative roots?
Assessment
- Lesson 5 Assignment
All assessment items you encounter need to be placed in your course folder.
Save a copy of the Lesson 5 Assignment to your course folder. You will receive more information about how to complete the assignment later in this lesson.
Materials and Equipment
- calculator
1.1. Launch
Module 5: Radicals
Launch
This section presents questions to help you determine if you have the skills and knowledge to complete this lesson successfully.
1.2. Are You Ready?
Module 5: Radicals
Are You Ready?
Answer the questions and check your solutions. If you are experiencing difficulty, you may want to use the information in the Refresher section to clarify concepts before moving on to the Discover section.
- Match each fraction on the left with an equivalent fraction on the right.
a.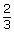 i.
i.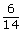
b.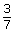 ii.
ii.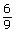
c.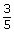 iii.
iii.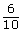
1.3. Refresher
Module 5: Radicals
Refresher
Visit Equivalent Fractions to find a definition of equivalent fractions and examples.
Go back to the Are You Ready? section, and try the questions again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 5: Radicals
Discover
You will recall from Lesson 4 that there are two general rules when dividing radicals:
You learned to calculate rational numbers and radicals separately when dividing them. When you are dividing radicals, there are three different methods that you can use to simplify the radical expressions:
- calculating rational numbers and radicals separately
- rationalizing the denominator
- eliminating common factors
Benito, Yvette, and Maria solved the same two questions, but each of them used a different strategy. Read “Example 3: Dividing radicals by a monomial” on pages 194 to 196 of your textbook. Pay close attention to each strategy for solving the same question.
Share 1
With a partner or in a small group, list the advantages and disadvantages of each strategy. Discuss which of the three strategies each of you prefers.
![]() Save your answers in your course folder.
Save your answers in your course folder.
1.5. Explore
Module 5: Radicals
Explore
When presenting a solution in mathematics, it is best to use an exact value rather than a calculated rounded approximation. This means solutions must often be left in radical form. The reason for this is simple: often when calculating a solution involving radicals, the answer is an irrational number whose decimal will never terminate and never repeat.
Fractions with radicals in their denominators are more complex than fractions that do not have a radical in their denominator. As you know in math, answers are given in the simplest form. The simplest form of a fraction would be to eliminate any radicals from the denominator. The process of determining an equivalent fraction that does not have any radicals in the denominator is called rationalizing the denominator.
When manipulating a fraction to create a new fraction, it is essential to end up with an equivalent fraction. Be careful that the method removes the radical from the denominator and gives you a fraction that is mathematically equivalent.
You learned many years ago that when you multiply any number by 1, you get the original number. You also learned that any number divided by itself is equal to 1.
These principles were introduced when you first learned equivalent fractions.
![]()
It is the same principle that will be applied when you create equivalent fractions by rationalizing the denominator.
The quickest way to eliminate a square root sign in the denominator is to multiply the radical by itself, which, of course, will result in the radicand ![]() . Remember that since you are working with fractions, whatever you do to the denominator must also be done to the numerator. So instead of multiplying by
. Remember that since you are working with fractions, whatever you do to the denominator must also be done to the numerator. So instead of multiplying by ![]() , you would multiply by
, you would multiply by ![]() .
.
Try This 1
The applet Rationalizing Denominators gives a series of steps that make it easy to rationalize the denominator.
As you saw in the applet, to rationalize the denominator in an expression, multiply both the denominator and the numerator by the expression that will eliminate the radical from the denominator.
To rationalize the denominator in ![]() , multiply both numerator and denominator by
, multiply both numerator and denominator by ![]() so the denominator is represented as an integer.
so the denominator is represented as an integer.
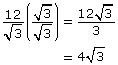
The radical expression is now simplified as far as possible, since there is no radical in the denominator and like terms are collected.
Given that ![]() , if you had to evaluate the expression without using a calculator, would you rather calculate
, if you had to evaluate the expression without using a calculator, would you rather calculate ![]() or
or ![]() ? Why is one preferred over the other if they are equal?
? Why is one preferred over the other if they are equal?
1.6. Explore 2
Module 5: Radicals
Self-Check 1
Rationalize the denominator in the following radical expressions.
-
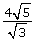 Answer
Answer
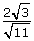 Answer
Answer
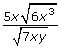 Answer
Answer
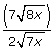 Answer
Answer
- The highest diving platforms at pools are 10 m above the water. The time a diver takes to hit the water in a pool is the same as diving off a cliff, and can be calculated using the radical equation
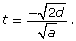
The distance is d = −10 m, and a, the acceleration due to gravity, is −9.81 m/s2. The negative numbers indicate the direction is downward. Use the general rule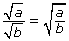 to rewrite the expression with a radical in the numerator and a radical in the denominator; then rationalize the denominator. Answer
to rewrite the expression with a radical in the numerator and a radical in the denominator; then rationalize the denominator. Answer

© Hristo Momcharov/10939305/Fotolia
When you square a negative number, the result is always positive; for example, (−5)2 = 25. The square root sign, however, indicates only the principal square root (or the positive square root) ![]() = 5 not −5. You likely noticed in this lesson that when diving into the ocean or into swimming pools, the distances were negative. In physics, positive and negative numbers indicate direction—positive is up, and negative is down. The distances have to be negative numbers because you can’t dive upwards into the water.
= 5 not −5. You likely noticed in this lesson that when diving into the ocean or into swimming pools, the distances were negative. In physics, positive and negative numbers indicate direction—positive is up, and negative is down. The distances have to be negative numbers because you can’t dive upwards into the water.
There may be times when you know that you want to have a negative value for an answer even though you are working with square roots. The negative square root is also called the secondary square root. When calculating expressions, how do you indicate that you want the secondary square root or negative root? How do you indicate that you want both the principal and secondary (positive and negative) square roots? You can use symbols in front of the radical signs to indicate exactly what you are looking for.
If you want only the principal (positive) square root, you use the radical sign with no symbols in front: ![]() , which equals x.
, which equals x.
If you want only the secondary (negative) square root, you put a negative sign in front of the radical sign: ![]() , which equals −x.
, which equals −x.
If you want both the principal and secondary (positive and negative) square roots, you put a plus or minus sign in front of the radical sign: ![]() , which equals ±y2.
, which equals ±y2.
Self-Check 2
Write the square root expression that is equal to each of the following numbers.
- −4
- ±8
- ±x3
- −ay4
If you haven’t done so already, now would be a good time to update your Glossary Terms document. Remember to save your updated document to your course folder.
The term to be added from this lesson is
- rationalizing the denominator
1.7. Connect
Module 5: Radicals
Connect
Lesson Assignment
Complete the Lesson 5 Assignment that you saved to your course folder.
Going Beyond

© Andrew Olkhovik/14542324/Fotolia
The world record height for a dive into water, held by Oliver Favre, is 53.9 m. Calculate how fast he was going when he hit the water. Search online to find where and when he achieved the record.
1.8. Lesson 5 Summary
Module 5: Radicals
Lesson 5 Summary
The key to rationalizing a denominator is to create an equivalent fraction that does not have a radical in the denominator. You learned very early in your math education that you could multiply any number or expression by 1 and get the same expression. Any fraction that has exactly the same value in both the numerator and the denominator is equal to 1. Therefore, to eliminate a radical in the denominator, you multiply both the numerator and the denominator by the radical, which is simply multiplying by 1. The final step is always to put the expression in its simplest terms.
When solving equations involving radicals, there are times when a negative answer is the only possible solution; but when you see a square root sign, you are only asked to give the principal (positive) square root of the radicand. If you are required to give a secondary (negative) square root, it will be indicated by a negative sign in front of the radical sign. If you are required to give both the principal and secondary square roots of a radicand, it will be indicated by a plus or minus symbol in front of the radical sign.
In the next lesson you will apply the skills you have been developing in this module to solve problems involving radical equations.