Lesson 6
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-2 SS |
| Book: | Lesson 6 |
| Printed by: | Guest user |
| Date: | Tuesday, 30 December 2025, 3:42 AM |
Description
Created by IMSreader
1. Lesson 6
Module 5: Radicals
Lesson 6: Solving Radical Equations
Focus

iStockphoto/Thinkstock
Have you ever come upon the scene of a traffic collision? Did you notice the skid marks? Perhaps you saw a police officer or crash investigator measuring the skid marks on the roadway. Why is it important to measure the skid marks at the site of a collision?
Crash team investigators measure the length of skid marks to calculate the speed of the vehicle when the brakes were first applied. Radical equations, such as ![]() and
and ![]() are used in their calculations. The calculations from these formulas are so accurate that the results are used as evidence if there is a court case regarding the traffic collision.
are used in their calculations. The calculations from these formulas are so accurate that the results are used as evidence if there is a court case regarding the traffic collision.
In this lesson you will learn to solve equations such as these that contain radicals. The first five lessons in this module have been preparation for this essential mathematical skill.
This lesson will help you answer the following inquiry questions:
- How do you determine the solutions (also known as roots) to a radical equation algebraically?
- How do you verify that the values determined in solving a radical equation are not extraneous roots of the equation?
Assessment
- Lesson 6 Assignment
All assessment items you encounter need to be placed in your course folder.
Save a copy of the Lesson 6 Assignment to your course folder. You will receive more information about how to complete the assignment later in this lesson.
Materials and Equipment
- calculator
1.1. Launch
Module 5: Radicals
Launch
This section presents questions to help you determine if you have the skills and knowledge to complete this lesson successfully. Before beginning this lesson you should be able to
- solve equations for the variable
- factor radical binomials and trinomials
1.2. Are You Ready?
Module 5: Radicals
Are You Ready?
Answer the questions and check your solutions. If you are experiencing difficulty, you may want to use the information in the Refresher section to clarify concepts before moving on to the Discover section.
Solve the following equations.
- 5x + 1 = 7 + 3x
- 4(x − 2) = 3(2x − 7)
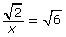
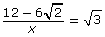
1.3. Refresher
Module 5: Radicals
Refresher
The basic rule used in solving equations in algebra is to balance both sides of the equation. In other words, what is done to one side of the equation must be done to the other side of the equation as well. For example, if you add a term on the left side, you must add the same term on the right side. If you multiply a term on the left side, you must multiply the same term on the right side. The following table shows how you can solve two different linear equations.
|
Solving a Basic Equation |
Solving by Combining Like Terms |
|
In the equation 6 = 3 − x, you want to get the x on the left side and the other items on the right side.
First, add x to both sides of the equation.
6 + x = 3 − x + x 6 + x = 3
Next, subtract 6 from both sides of the equation.
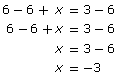
By following these two steps, you learn that x = −3, which is the solution to the equation. |
Consider the equation 2x + 3 = −4x − 7.
You can solve the equation by first getting all the x-terms on the left side.
Add 4x to both sides.
2x + 4x + 3 = −4x + 4x − 7
Combine like terms.
6x + 3 = −7
Subtract 3 from both sides.
6x + 3 − 3 = −7 − 3
Combine like terms.
6x = −10
Divide both sides by 6.
Simplify the fraction.
|
Try the “Algebra Four!” equations game to practise your equation-solving skills. You can choose different types of questions to practise. Select “Two-Step Problems,” and then play one round. Next, you can add “Variable on Both Sides” the second time you play. This game is best played with two people, so you may want to invite a classmate to play with you, or perhaps your teacher or a parent may be willing to play with you. If you feel up to the challenge, you can select the first, second, and fourth options. (Do not select the “Quadratic” option, as you will be learning how to solve quadratic equations in a future course.) As a helpful hint, if you try the game, you may need to have a piece of paper and a pencil handy.
© Shodor
If you had trouble factoring the expressions, work through the Factoring Special Products gizmo.
Screenshot reprinted with permission of ExploreLearning.
Go back to the Are You Ready? section, and try the questions again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 5: Radicals

iStockphoto/Thinkstock
Discover
When there has been an accident, police investigators photograph and measure the length of skid marks to help determine what happened. Equations containing radicals in the calculations are used to find the speed of the vehicles involved.
Try This 1
Go to Radical Equations: Introduction to complete the table of values that will help a police officer investigate a car crash. First, choose “Radical Equations.” Then, select the arrow button. Complete the “Introduction.”
1.5. Explore
Module 5: Radicals
Explore

© swisshippo/32497251/Fotolia
You were able to determine that if the driver was going 50 km/h, the skid marks should be 20 m long. What if, however, the driver had been going a different speed that didn’t show up in the table of values you created? If you could just rearrange the equation to solve for d and substitute in the value for s, you could easily determine the correct skid mark length at any given speed.
Try This 2
The Radical Equations: Tutorial applet will help you discover how to solve equations that have variables under the radical sign. You may be required to enter a username and a password. Then, choose “Radical Equations.” At the new page, select the tutorial icon: it is the icon at the top of the page that is shaped like a blackboard. This will take you to a tutorial menu page. Work through the five tutorial pieces.
Read “Example 1: Using inverse operations to solve radical equations” on pages 216 to 218 of your textbook. Look closely at the process used to determine the solutions. How important is it that you verify your answer by substituting back into the original equation?
Self-Check 1
-
What restrictions are there on the values of the variables in each of the following equations if the equations involve real numbers? Solve and check each of the equations to make sure there are no extraneous roots.
extraneous root: a root, which is also called a solution, that appears to be a solution to an equation but does not satisfy the conditions that were originally introduced
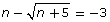 Explain why there is an extraneous root in this instance.
Explain why there is an extraneous root in this instance.
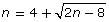
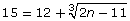
Answers
- Complete “Check Your Understanding” question 3 and “Practising” questions 4 and 5 on page 222 of your textbook. Answers
1.6. Explore 2
Module 5: Radicals
Try This 3
Use the Radical Equations: Examples applet to build your skills at solving radical equations. You may be required to submit a username and a password. Next, select “Radical Equations.” Then choose the examples icon, which is shaped like a puzzle piece. This will take you to an examples menu page. Complete all three of the activities.
If you haven’t done so already, now would be a good time to update your Glossary Terms document. Remember to save your updated document to your course folder.
The term to be added from this lesson is
- extraneous root
1.8. Lesson 6 Summary
Module 5: Radicals
Lesson 6 Summary

iStockphoto/Thinkstock
When you are solving radical equations, the first consideration is to determine whether there are restrictions on the variable. Recall from previous lessons that you always determine restrictions on the original equation. Not all numbers can be used for variables in a radical equation. If the radicand is in the denominator, the value of the radicand cannot allow the denominator to equal zero. Also, if the index is an even number, the radicand must not have a negative value.
The first step in solving a radical equation is to isolate the radical. Once the radical is isolated, you can eliminate the radical sign. To do this, you square both sides of the equation (i.e., if the radical is a square root) or cube both sides of the equation (i.e., if the radical is a cube root). Once you have eliminated the radical sign, you solve for the variable using algebra. This may involve using inverse (or opposite) operations, or it may involve factoring trinomials.
Sometimes in the process of solving a radical equation, you can find a root (also called a solution) that is not a solution to the original equation. This is known as an extraneous root. As you discovered in the Explore section, the process of squaring both sides of an equation changes the possible solution set from those values that lie on a portion of a parabola to those values that lie on an entire parabola. The only way to be sure which roots are solutions is to substitute the roots one at a time into the original equation. If both the left side and right side of the equation are equal, the root is a solution to the equation. If both sides are not equal when the root is substituted in, the root is extraneous (not a solution).
In the next lesson you will model situations using radical equations. You will use the ability to solve the equations that you developed in this lesson to answer questions about that situation.