Lesson 7
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-2 SS |
| Book: | Lesson 7 |
| Printed by: | Guest user |
| Date: | Saturday, 6 September 2025, 2:36 AM |
Description
Created by IMSreader
1. Lesson 7
Module 5: Radicals
Lesson 7: Modelling Problems with Radical Equations
Focus
Hemera/Thinkstock
The length of one year on a planet is equal to the time it takes that planet to complete one orbit of its star. It takes Earth 365 days to orbit its nearest star, the Sun. It only takes the planet Mercury 87.96 Earth days to complete one orbit of the Sun, so a year on Mercury is much shorter than a year on Earth. The planet Jupiter takes 11.83 Earth years to complete its orbit of the Sun, so a year on Jupiter is much longer than a year on Earth.
The relationship between a planet’s orbit and its distance from the Sun was discovered by Johannes Kepler in 1619. He proved that the farther a planet is from the Sun, the longer it takes to complete one orbit (called the period). This relationship, known as Kepler’s third law, states that the square of the orbital period is proportional to the cube of the distance the planet is from the Sun and is represented by the following equation:
T2 = Kr3
If you isolate the period, T, you get 
where T is the orbital period (the time it takes to make a single orbit), K is a proportionality constant, and r is the maximum distance from its star.
As you have seen throughout this module, radical expressions are used to solve problems in many situations. In this lesson you will use radical equations to model different situations in order to solve problems. You will see that radical equations can not only be used to find the length of a year on different planets but also to find the dimensions of a soccer field, the amount of current in a hair dryer, or how to find the dimensions of a TV screen. These are, of course, only a few examples of the use of radicals.
This lesson will help you answer the following inquiry question:
- How do you use radical equations to model situations when solving problems?
Assessment
- Lesson 7 Assignment
All assessment items you encounter need to be placed in your course folder.
Save a copy of the Lesson 7 Assignment to your course folder. You will receive more information about how to complete the assignment later in this lesson.
Materials and Equipment
- calculator
1.1. Explore
Module 5: Radicals
Explore
© Yevheniy Kotsaryev/32788027/Fotolia
When solving problems in math, the key to success lies in translating the word problems into mathematical symbols. Some problems give both the equation and the values needed to solve the equation.
Read “Example 2: Modelling a situation with a radical equation” on pages 219 to 221 of your textbook. In this example, the equation is given. Ramesh and Nicola used two different processes and still calculated the same answer.
Share 1
With another student or appropriate partner, discuss the differences between Ramesh’s and Nicola’s solutions.
- Which method would you choose?
- Both Ramesh and Nicola began by stating the restrictions on the variables. In Lesson 6 you looked at the importance of stating restrictions on variables. Why is the formula only defined if L is greater than or equal to zero?
Place a copy of your answers in your course folder.
1.2. Explore 2
Module 5: Radicals
There are times where you are given information about a situation, and you need to combine different formulas to develop an equation that will solve the problem.
The length of a soccer field is 
times the width. The diagonal of the field is 116.6 yd long.
What are the dimensions of the soccer field to the nearest yard?
Watch Soccer Field to see how the dimensions of the soccer field are determined.
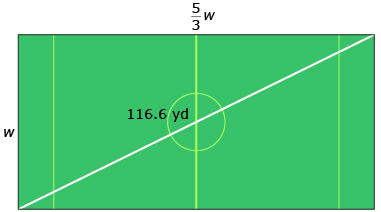
Begin by stating any restrictions on variables. Then sketch a diagram and label it with any information that you have:
- w ≥ 0
- The diagonal is 116.6 yd.
- The width is unknown: let the width = w.
- The length is
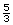times the width: let the length = 
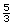w.
The Pythagorean theorem can be used to set up an equation.
a2 + b2 = c2
Now the equation can be rearranged to isolate w.
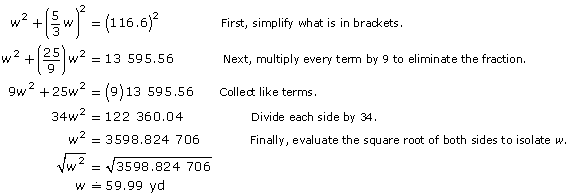
The answer should be rounded to the nearest yard, so w = 60 yd.
Since 
the length of the soccer field can be calculated:
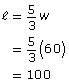
The width of the soccer field is 60 yd, and the length is 100 yd.
1.3. Explore 3
Module 5: Radicals
Hemera/Thinkstock
In the early 1600s, Galileo discovered that the swinging motion of a pendulum does not change even if the width of the swing changed or the weight at the bottom of the pendulum changed. He found that it was the length of the pendulum that determined its period of motion.
Self-Check 1
- Galileo discovered that the time for a complete back-and-forth swing of a pendulum (called one period) is directly proportional to the square root of the length and inversely proportional to the square root of the acceleration due to gravity. The constant of proportionality is 2π. Another way of saying this is that the period is 2π times the square root of the pendulum length divided by the square root of acceleration due to gravity.
- Write an equation expressing the relationship between the period T of a pendulum and its length. Use L for length and g for the acceleration due to gravity. Notice how the variables are chosen to indicate what each represents. State any restrictions on the variables.
- A pendulum in a wall clock has a length of 1.4 m. What is the period of that pendulum to the nearest hundredth of a second if the acceleration due to gravity is 9.81 m/s2?
- Find the length of a pendulum that will give a period of 2 s. This means that the clock will tick precisely every second, at each end of the
back-and-forth swing of the pendulum.
- Write an equation expressing the relationship between the period T of a pendulum and its length. Use L for length and g for the acceleration due to gravity. Notice how the variables are chosen to indicate what each represents. State any restrictions on the variables.
-
The power in watts (W) of a hair dryer is equal to the ratio of the current in amps (A) squared multiplied by the resistance in ohms (Ω).
Christopher Robbins/Photodisc/Thinkstock- Express the statement as an equation, where power is P, current is I, and resistance is R.
- Rearrange the equation to isolate current, I.
- How much current flows through a 1600-W hair dryer that has a resistance of 8.82 ohms?
iStockphoto/Thinkstock
- Express the statement as an equation, where power is P, current is I, and resistance is R.
- Most new TV screens have a 16:9 aspect ratio. This means the width is
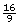times the height. When a television is advertised as having a 42-in screen, it means the length of the diagonal of the screen is 42 in.-
Determine the height of a 42-in screen. Begin by letting the height be h. Then express the width in terms of height. In your answer, include a
- description of any restrictions on the variables
- drawing using your variables and putting in the length of the diagonal
- description of any restrictions on the variables
Use the Pythagorean theorem to set up an equation and solve for the height.
Is your answer reasonable?
- Determine the width of a 42-in screen. How can you check your answer?
- What is the total viewing area of a 42-in screen?
-
Determine the height of a 42-in screen. Begin by letting the height be h. Then express the width in terms of height. In your answer, include a
- Complete “Practising” questions 11, 12, 13, and 14 on pages 223 and 224 of your textbook.
Answer
Read “Frequently Asked Questions” on pages 226 and 227 of your textbook. If you have any additional questions about solving problems with radical equations, be sure to contact your teacher.
If you have not already done so, now would be a good time to add important concepts to your notes organizer that you have saved to your course folder.
1.5. Lesson 7 Summary
Module 5: Radicals
Lesson 7 Summary
iStockphoto/Thinkstock
Radical equations are used to solve problems in many situations. The key to success lies in translating the word problems into mathematical symbols. Some problems give you both the equation and the values needed to solve the equation. You can then state any restrictions on the variables and proceed to solve the equation. There are, however, problems where you are given information about a situation and you need to combine different formulas to develop an equation in order to solve the problem.
When you solve a radical equation, you will use inverse operations to first isolate the radical and then eliminate the radical sign. Before you solve the equation, you need to state any restrictions on any variables provided. This ensures that the radicand of a square root is not negative or that the answer is reasonable. For example, if you are solving a problem about the distance from a planet to the Sun, you need to state that the answer cannot be negative because distances are not negative.
In the process of solving radical equations, you often need to square a radical to remove the radical sign. This may, however, introduce an invalid solution called an extraneous root; so you need to verify each solution by substituting it back into the original equation.
You have used radical expressions and equations to help solve a variety of problems. Now refer to the Module 5 Summary for an overview of concepts you investigated in this module.