Module 5 Project
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-2 SS |
| Book: | Module 5 Project |
| Printed by: | Guest user |
| Date: | Tuesday, 30 December 2025, 5:37 AM |
Description
Created by IMSreader
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-2 SS |
| Book: | Module 5 Project |
| Printed by: | Guest user |
| Date: | Tuesday, 30 December 2025, 5:37 AM |
Created by IMSreader
In this project you will work with dot paper to drawing straight and tilted squares and calculate their areas and side lengths.
It is difficult to visualize a line that is ![]() or
or ![]() long. You will be using 1-cm dot paper to draw squares with different areas and finding the lengths of line segments between dots on the grid. This project will give you a greater understanding of radicals and help you to see that
long. You will be using 1-cm dot paper to draw squares with different areas and finding the lengths of line segments between dots on the grid. This project will give you a greater understanding of radicals and help you to see that ![]() are numbers as real and definite as 2 or 5.
are numbers as real and definite as 2 or 5.
There are three parts to your assignment. All three parts must be handed in to your teacher.
|
Part 1 |
20 marks |
|
Part 2 |
30 marks |
|
Part 3 |
20 marks |
|
Total Marks |
70 marks |
Refresh your memory of some skills needed for the project by completing the following section.
Assume the dots on the figure are exactly 1 cm apart.
If you successfully completed the Are You Ready? questions and feel comfortable with the concepts, move on to Part 1 of the project.
If you experienced difficulties with the questions, use the resources in the Refresher to review the prerequisite concepts before continuing through the lesson.
Visit Pythagorean Theorem to find a definition, examples of how it is used, and a demonstration applet.
Go back to the Are You Ready? section, and try the questions again. If you are still having difficulty, contact your teacher.
You may work with a partner or as a small group on this activity; however, each person must submit his or her own answers as part of the project submission.
You can choose to print out 1-cm Dot Paper and draw squares on grid paper, or you can use the Geoboard applet. To draw squares using the applet, drag either or both of the red dots. The area of the square created will be shown inside the square.
Using the applet or grid paper, draw squares that have the areas listed in Table 1. Give the exact length of each side of the square. (20 marks)
![]()
There are different ways to find the exact area of a tilted square. Measurement is not one of the methods because a measurement is always an approximation.
Look at the following diagram for one possible way of finding the exact location of a tilted square.
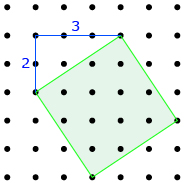
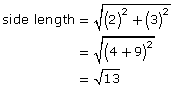
![]()
Remember to save your completed Table 1 to your course folder. You will submit it to your teacher for marks at the end of Lesson 3. At this time, you should read the Lesson 1 Summary.
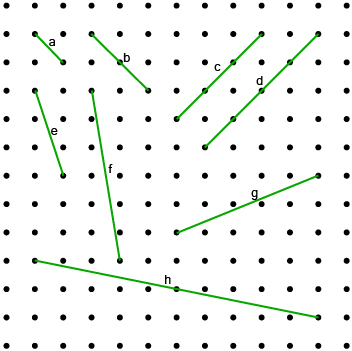
Segment |
Exact Side Length (cm) |
a |
|
b |
2 |
c |
|
d |
|
e |
0.5 |
f |
|
g |
10 |
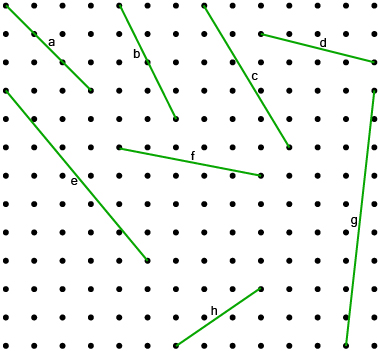
Segment |
Exact Side Length (cm) |
h |
|
i |
|
j |
15 |
k |
|
l |
|
m |
|
n |
|
Remember to save your work from Part 2 to your course folder. You will submit it to your teacher for marks at the end of Lesson 3. At this time, you should read the Lesson 2 Summary.
For the summary of the Module 5 Project, complete the following questions.
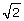 in length. Now draw a line segment that is
in length. Now draw a line segment that is 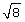 in length. How do the two line segments compare? (2 marks)
in length. How do the two line segments compare? (2 marks)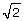 in length. Now draw a line segment that is
in length. Now draw a line segment that is 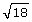 in length. How do the two line segments compare? (2 marks)
in length. How do the two line segments compare? (2 marks)Submit to your teacher the following completed documents for your assessment of the project.