Lesson 1
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-2 SS |
| Book: | Lesson 1 |
| Printed by: | Guest user |
| Date: | Tuesday, 30 December 2025, 5:35 AM |
Description
Created by IMSreader
1. Lesson 1
Module 6: Proportional Reasoning
Lesson 1: Comparing and Interpreting Rates
Focus
Being able to compare items and interpret the results is a valuable skill. Understanding when items can and should be compared is part of that skill. Sometimes, people try to compare items that have no real connection to one another.
Have you ever heard the expression “comparing apples to oranges”? This expression is used when someone is trying to compare two different things that are not closely related. As a result, a person will not be very successful with the comparison.
For example, comparing the colour of a car to the litres per hundred kilometres that the car gets doesn’t make any sense—it is like comparing apples to oranges. On the other hand, comparing the litres per hundred kilometres that a car gets to the type of engine that it has could be of value since there is a connection between the type of motor and how much fuel is used. This kind of comparison is useful and it may help someone decide which car to purchase.

iStockphoto/Thinkstock
Different strategies can be used to compare items. One strategy is to use rates. In your grade eight mathematics courses you learned how to calculate rates. In this lesson you will use rates to compare different items. Rates can help you determine which item is the cheapest, which item is the best buy, or which item is best suited for a specific situation.
This lesson will help you answer the following inquiry questions:
- How can rates be used to represent, interpret, and compare different items and/or situations?
- How can rates be used to solve problems?
Assessment
- Try This 2
This lesson provides you with opportunities to investigate, review examples, and practise the knowledge and skills you are learning. For instance, in Are You Ready? and Self-Check, you can check your answers to see if you are on track. If you are having difficulty with concepts or calculations, contact your teacher.
All assessment items you encounter need to be placed in your course folder. You should have already had a discussion with your teacher about which items you will be handing in for marking. Make sure you follow your teacher’s instructions.
Save a copy of the Lesson 1 Assignment to your course folder. You will receive more information about how to complete the assignment later in this lesson.
Time
Each module is made up of lessons. Each lesson in Mathematics 20-2 is designed to be completed in approximately 80 minutes. You may find that you require more or less time to complete different lessons depending on your strengths. It is important that you progress at your own pace based on your individual learning requirements.
Materials and Equipment
- calculator
1.1. Are You Ready?
Module 6: Proportional Reasoning
Are You Ready?
In previous mathematics courses you learned about proportional reasoning. You learned how to calculate rates and about equivalent ratios. Use the “Rates and Ratios” applet to check your understanding of equivalent ratios and writing ratios. First, select “Rates and Ratios (Food)” under the “Number” heading. Next, click on the “Topics” tab. Then choose the following:
- “Topic 1: Equivalent Ratios”
- “Topic 2: Writing a Ratio”
If you feel you need more of a review of these topics, refer to the Refresher section in this lesson.
1.2. Refresher
Module 6: Proportional Reasoning
Refresher
Recall that a ratio is a comparison of numbers or quantities. For example, the ratio of red marbles to blue marbles in the following diagram could be expressed in the following ways:
![]()
- 2 to 4
- 2:4
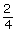
The ratio 2:4 can be written in lowest terms as 1:2. The ratio 2:4 is said to be equivalent to the ratio 1:2. In other words, 2:4 = 1:2. Equivalent ratios can be written in any of the forms that ratios can be written.
- 1:2
- 1 to 2
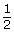
A ratio can compare numbers with the same or different units. Consider the following three plates. Each plate has four slices of pizza on it.
![]()
The ratio of slices of pizza to plates could be expressed as
- 12 to 3
- 12:3
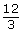
The ratio of slices of pizza to plates could also be expressed in lowest terms as 4:1.
These ratios have different units for each part of the ratio. Here the ratio represents the number of slices of pizza to the number of plates (4 slices of pizza to 1 plate).
A proportion is made up of two or more ratios that are equivalent.
![]()
Proportions can be used to solve for unknown values. For example, you could use the ratio of the 12 slices of pizza to 3 plates to set up a proportion to determine how many slices of pizza (p) would be on 20 plates if the pizza was arranged the same on all 20 plates.
Begin by writing a proportion with the unknown value represented by a variable. Use p to represent the pizza slices.
![]()
To find the number of slices of pizza, you need to isolate the variable, p.
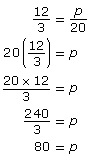
There are 80 slices of pizza on 20 plates.
For more information on proportion and how ratios can be used to solve problems, refer to the Proportion definition.
1.3. Discover
Module 6: Proportional Reasoning
Discover

iStockphoto/Thinkstock
The expression “comparing apples to oranges” illustrates that, when comparing items, you must be aware of exactly what you are comparing. In other words, what is the purpose of your comparison? For instance, if you are trying to determine which brand of apples costs less, it is of no use to you to compare the prices of one brand of apples and one brand of oranges. You need to compare apples to apples.
Rates can be used to compare items. Recall that a rate is a ratio that has two terms that are measured in different units. The price of produce is commonly expressed as a rate, but the way that stores mark their prices sometimes makes it difficult to find the best value. For instance, the price of a bag of red apples is expressed as the rate $4.95/5 lbs. The price of a bag of green apples is expressed as the rate $4.95/2.27 kg. Both bags are the same price, but the units are different—5 lb versus 2.27 kg.
![]()

By only looking at the marked price of items, it isn’t always easy to determine which item is the best buy or has the best value. Both the red apples and the green apples are priced at $4.95.
Find something that the items have in common so you can compare them. Often when comparing items, you can calculate equivalent ratios that have the same unit in the second term of the ratio. If the second term of the ratio is 1, it is called a unit rate. In other words, a unit rate has a denominator of 1.
unit rate: a rate in which the numerical value of the second term is 1
For example, $4.50/6 bottles of pop expressed as a unit rate is $0.75/bottle. (When the second term is 1, it is not necessary to write the number, only the units.)
—Source: CANAVAN-MCGRATH ET AL. Principles of Mathematics 11, © 2012 Nelson Education Limited. p. 455. Reproduced by permission.
To determine the unit rate, divide the numerator by the denominator of the rate (or express the rate in its lowest terms). For example, the price of apples can be represented using a unit rate expressed as dollars per pound or dollars per kilogram as shown.

Red Apples: Brand X Pictures/Thinkstock; Green apples: Photos.com/Thinkstock
Although both types of apples have been expressed as a unit rate, you still can’t compare them as you are not using the same units in the second term. Instead, the apples are being compared price per pound to price per kilogram. In order to compare the value, the same units need to be compared.
Change the price of the red apples to be in $/kg. You know that 1 kg = 2.2 lb.
![]()
On the left side of the equation, lb on the bottom left will cancel out lb on the top right.
The unit rates of both the red apples and the green apples are the same, $2.18/kg, so both bags of apples have the same value.
Self-Check 1
Use the “Rates and Ratios (Food)” applet again to change various rates into unit rates. This time you will select “Topics” and choose “Topic 3: Rates and Unit Rates.”
1.4. Discover 2
Module 6: Proportional Reasoning
People use rates every day to help them get the best value on their purchases. For example, many of the decisions that have to be made during the moving process can be made by comparing rates. Rates and unit rates can help determine which moving company is the most cost effective, which type of snack for the road is the best buy, which vehicle has the best fuel consumption, or who can pack the fastest.
Consider the following situation.

Comstock/
Thinkstock
Rajesh and his family are preparing to move to a new city. As part of their move preparation, Rajesh is responsible for filling up the family vehicles with gas. His brother Kunal is responsible for picking up snacks and beverages for the drive.

water bottle: iStockphoto/Thinkstock; gas can: iStockphoto/Thinkstock; coin: Coin image © 2011 Royal Canadian Mint – All Rights Reserved
Try This 1
You should place your completed Try This activities in your course folder. Your teacher may ask to see your completed Try This activities. For more information on Try This activities, refer to the Course Introduction.
It costs Rajesh $53.02 to put 55 L of fuel in his mom’s car. It costs Kunal $5.64 for a pack of 12 500-mL water bottles. Kunal makes the comment that bottled water is actually more expensive than fuel. Rajesh thinks he is wrong. Rajesh says that fuel costs more than bottled water.
- Compare the cost of the fuel to the cost of the bottled water.
- Do you agree with Kunal or with Rajesh? Explain your reasoning.
Share 1
After a discussion with your teacher, you will decide how to connect with other students for Share activities. Follow your teacher’s instructions to complete this Share activity. Place a summary of your Share discussion in your course folder. For more information on Share discussions, refer to the Course Introduction.
Share your comparisons from Try This 1 with another student or appropriate partner. Consider the following:
- What methods did you each use to compare the cost of fuel to the cost of the bottled water? How were the methods similar? How were they different?
- Describe your conclusions about whether Kunal or Rajesh was correct. What was the reasoning behind your decisions?
1.5. Explore
Module 6: Proportional Reasoning
Explore
Rates can be compared by using one of the following two methods:
- Compare the rates using the same unit where the second terms are numerically the same.
- Write the rates as unit rates where the second terms are the same units and are equal to 1.
For instance, in Try This 1, you may have chosen to compare rates or you may have chosen to compare unit rates to determine whether fuel is more expensive than bottled water. You might have calculated the cost of each item per litre (unit rate), or you might have determined the cost per 500 mL (rate). You might also have determined how much it would cost for 55 L of bottled water and then compared that to the price of 55 L of gas.
Each of these strategies is correct. The key in comparing rates is to be certain that you are comparing the same things. Remember that you can’t compare apples to oranges.
Read “Example 1: Comparing two rates expressed in different units” on pages 445 and 446 of your textbook. As you read, consider how the strategies used in Natasha’s and Dimitri’s solutions compare to the strategy you used to determine whether fuel or bottled water had the lower price.
Self-Check 2
Complete “Practising” questions 4, 5, 7, and 8 on page 451 of your textbook. Answer
The lowest rate is not always the most appropriate rate. In the price examples you looked at earlier in this lesson, you were trying to determine which item had the lowest rate or unit rate. In other words, you wanted to determine which item cost the least amount of money or was the best buy. So you wanted the lowest rate or unit rate. In some cases, the higher rate is preferred.

Comstock/
Thinkstock
Rajesh and his family were thinking of making a trip to the United States. Rajesh knew that they would need to purchase some American dollars for the trip. His bank posts the exchange rate that gives the value of one Canadian dollar compared to the value of one American dollar.
The first time he checked the currency exchange, Rajesh found $1.00 Cdn was worth $1.023 601 U.S. This meant he would get $1.02 U.S. for every Canadian dollar he exchanged. The next week when he checked, he found that $1.00 Cdn was worth $1.035 501 U.S. He realizes that, at this exchange rate, he could exchange $1.00 Cdn for $1.04 U.S. In this case, Rajesh was looking for a higher rate so he would get more American money for his Canadian money when he went to exchange the money.

Canadian money: Stockbyte/Thinkstock; American money: BananaStock/Thinkstock
Share 2
With another student or appropriate partner, identify three other situations where a higher rate or higher unit rate would be preferred. For each situation, determine what type of rate would be used to represent the situation.
Self-Check 3
1.6. Explore 2
Module 6: Proportional Reasoning
iStockphoto/Thinkstock
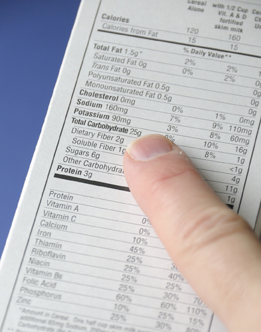
In some cases, the unit rate is not the most appropriate rate to use to represent or to compare items. Nutritional content of foods is one example where the unit rate may not be the best choice. The nutrition-facts label on food is based on a specific serving size. Representing the nutritional content as a rate per serving as opposed to a unit rate (e.g., amount per gram) helps consumers to be better informed as to the nutritional content of what they are eating.
For example, the serving size of a particular brand of cereal is ![]() of a cup, or 49 g. The nutrition facts on the side of the box are based on this serving size. The table shows the nutrition content given as a rate (per serving) and as a unit rate (per gram).
of a cup, or 49 g. The nutrition facts on the side of the box are based on this serving size. The table shows the nutrition content given as a rate (per serving) and as a unit rate (per gram).
|
Rate (per serving) |
Unit Rate (per gram) |
|
|
1 g of cereal |
|
Calories |
200 cal to
|
4.08 cal/g
|
|
Total Fat |
7 g to
|
0.14 g/g
|
|
Sugar |
15 g to
|
0.31 g/g
|
|
Protein |
4 g to
|
0.08 g/g
|
Is it easier to visualize ![]() of a cup of cereal or 1 g of cereal? For representing the nutritional content of foods, it is more appropriate to use a rate per serving as opposed to a unit rate.
of a cup of cereal or 1 g of cereal? For representing the nutritional content of foods, it is more appropriate to use a rate per serving as opposed to a unit rate.
1.7. Explore 3
Module 6: Proportional Reasoning
Sarah and her sister Susan were each making a pitcher of iced tea to drink with supper.

Zedcor Wholly Owned/PhotoObjects.net/Thinkstock
When they put their iced tea on the table, they noticed that the iced tea in Susan’s pitcher was much darker than Sarah’s. Why was this? The following Math Lab will help you to answer this question.
Math Lab
Work through Food Colouring. You will be given the opportunity to perform experiments to assist you in making predictions about changing rates.
Self-Check 4
Answer the following questions based on overall observations that you made from the experiments you completed in the Math Lab.
- When more drops of food colouring were added, did the concentration of food colouring to water increase or decrease? Answer
- When more water was added, did the concentration of food colouring to water increase or decrease? Answer
- Is using a unit rate an appropriate way to compare concentrations here? Why or why not? Answer
When dealing with rates, it is important to use an appropriate rate for the situation. You have looked at examples where a unit rate is most useful, situations where comparing rates per serving size is best, and examples where comparing with a common number for the second term of the rate is the easiest way to compare.
1.8. Explore 4
Module 6: Proportional Reasoning
Try This 2
Go to the Lesson 1 Assignment that you saved to your course folder. Complete Try This 2 at this time. Remember to save your updated Lesson 1 Assignment to your course folder when you have completed Try This 2.

Comstock/
Thinkstock
Rajesh and Kunal packed up their bedrooms in preparation for their family’s move. They timed how long it took each of them to pack.
- Using the following graphic, determine who was the faster packer: Rajesh or Kunal. (4 marks)
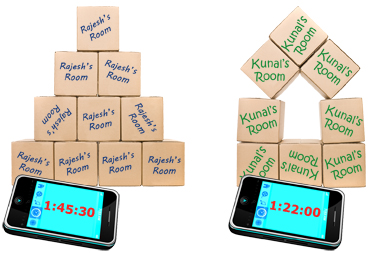
boxes: iStockphoto/Thinkstock; smart phone: iStockphoto/Thinkstock
- Identify any factors that could affect their packing rates, and explain the effect that these factors would have on the packing rate (i.e., increase or decrease). (2 marks)
1.9. Explore 5
Module 6: Proportional Reasoning
![]()
As you have seen in this lesson, different strategies can be used to interpret and compare rates. The purpose of the comparison needs to be considered when determining what type of rate to use in a given situation. Some rates are easier to understand and visualize than others. For instance, the packing rate for moving boxes could have been represented as minutes per box, boxes per minute, or boxes per hour.

Brand X Pictures/Thinkstock
It is hard to visualize 0.095 of a moving box. In this situation, it would be more appropriate to compare the packing rate as the number of minutes it takes to pack one box or the number of boxes that can be packed in one hour.
Self-Check 5

iStockphoto/Thinkstock
- Trinity and her friends are trying to determine who among them can text the fastest. They each typed a text message into their cellphones. The following table shows their results.
Trinity
3 words/12 s
Josh
4 words/18 s
Juanita
1 word/5 s
1.10. Lesson 1 Summary
Module 6: Proportional Reasoning
Lesson 1 Summary
The expression “comparing apples to oranges” illustrates that when comparing items, you first have to identify the purpose of your comparison. In some situations, a rate can be used to interpret or compare items. In others, a unit rate is more appropriate. For example, if you were trying to determine which brand of mouthwash was the best buy, you might determine the cost per 100 mL as opposed to the cost per millilitre. Even though the rates are equivalent, it is easier to visualize 100 mL of mouthwash as opposed to 1 mL of mouthwash.

Hemera/Thinkstock
Likewise, the lowest rate is not always the most appropriate rate. When determining which item is cheaper, you are looking for the lowest rate. Internet connection speed is an example of a situation where you want a higher rate. The faster the rate at which information is transferred over the computer network, the happier you are likely to be.
There are many factors that can influence a rate. These factors may decrease or increase a rate. For example, the rate at which a vehicle travels (speed) can be affected by road conditions, the weather, experience of the driver, and condition of the vehicle.
In Lesson 2 you will use graphs to represent rates and continue to use rates to solve problems.



