Lesson 4
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-2 SS |
| Book: | Lesson 4 |
| Printed by: | Guest user |
| Date: | Saturday, 6 September 2025, 2:39 AM |
Description
Created by IMSreader
1. Lesson 4
Module 6: Proportional Reasoning
Lesson 4: Scale Factor
Focus
© Glenda Powers/#6260390/Fotolia
Road trips are an opportunity to visit some amazing local attractions or to experience local history. In the Black Hills of South Dakota, the Crazy Horse Memorial is an example of history on a large scale.
Sculptor Korczak Ziolkowski and Lakota Chief Henry Standing Bear officially started the Crazy Horse Memorial on June 3, 1948. The Memorial’s mission is to honor the culture, tradition and living heritage of North American Indians. The original Crazy Horse sculpture depicts the Lakota warrior, Crazy Horse, seated on his horse and pointing over the horse’s head as he says, “My lands are where my dead lie buried.”1
In order to create the Crazy Horse Memorial, a small model was first sculpted by Mr. Ziolkowski. He used this small model to create a larger model, which is an exact scale enlargement of the original sculpture. The final monument on the mountain will be a very large duplicate of these sculptures. When completed the Crazy Horse mountain carving will be 641 ft long by 563 ft high (approximately 195.4 m by 171.6 m). Crazy Horse’s completed head is 87 ft 6 in (26.67 m) high. The horse’s head is 219 ft (66.8 m) or 22 stories high.
This lesson will help you answer the following critical question:
- How can scale factor be used to produce proportional 2-D shapes or 3-D objects?
Assessment
Did You Know?
The Crazy Horse Memorial is a carving on a massive scale! For more information on the memorial and the museum, including a video of the explosive engineering that is being used to carve the mountain, type “Crazy Horse Memorial” into your favourite Internet search engine. The Crazy Horse Memorial webpage also has webcams, photo galleries, and more information on the carving process.
While you will not be handing in any work from Lesson 4 for marking, the activities in this lesson will prepare you for other assignments in this module.
Materials and Equipment
- calculator
- ruler
1Crazy Horse Memorial Foundation
1.1. Explore
Module 6: Proportional Reasoning
Explore
proportional: two quantities that are related by a constant ratio
similar objects: two or more 3-D objects that have proportional dimensions
— Source: CANAVAN-MCGRATH ET AL. Principles of Mathematics 11, © 2012 Nelson Education Limited. p. 483. Reproduced by permission.
The process of carving a mountain is long and complex. The Crazy Horse Memorial has been in the works since the late 1940s. Before any work on the mountain began, Mr. Ziolkowski created a sculpture of his dream. In order for Crazy Horse to look realistic, Mr. Ziolkowski needed to make sure the sculpture was proportional. In other words, the sculpture’s measurements needed to be proportional to the actual measurements of Crazy Horse and his horse. This means that the model sculptures and the finished memorial are similar objects.
c Ragnar Schierholz /flickr; attribution, non-commercial
scale diagram: a drawing in which measurements are proportionally reduced or enlarged from actual measurements; a scale diagram is similar to the original
enlarge: to increase the dimensions of an image or object by a constant factor
reduce: to decrease the dimensions of an image or object by a constant factor
— Source: CANAVAN-MCGRATH ET AL. Principles of Mathematics 11, © 2012 Nelson Education Limited. p. 466. Reproduced by permission.
scale: the ratio of a measurement on a diagram to the corresponding distance measured on the shape or object represented by the diagram
A scale is a ratio or rate, so it always includes units.
— Source: CANAVAN-MCGRATH ET AL. Principles of Mathematics 11, © 2012 Nelson Education Limited. p. 466, 467. Reproduced by permission.
scale factor: a number created from the ratio of any two corresponding measurements of two similar shapes or objects, written as a fraction, a decimal, or a percent
— CANAVAN-MCGRATH ET AL. Principles of Mathematics 11, © 2012 Nelson Education Limited. p. 467, 470. Reproduced by permission.
Scale diagrams of 2-D shapes and scale models of 3-D objects are used to ensure proportionality when an object is enlarged or reduced.
Mr . Ziolkowski created scale models in preparation for carving Crazy Horse into the mountain. When the team started carving Crazy Horse’s head into the mountain, a 60-ft-long measuring boom was used to transfer measurements from a 1:34 scale model to the mountain.
Recently, laser scanning methods have been used to measure the 1:34 and 1:300 scale models. The 1:300 scale model is 
the size of the carving on the mountain, so every aspect of the carving is 300 times larger than the model. In other words, if you lined up 300 of the smaller scale models, their lengths would be the same as the length of the final monument.
Even with technological advancements in surveying, the steps involved in carving the mountain remain the same.
Step 1: Measure the scale model.
Step 2: Measure the mountain.
Step 3: Remove all the rock that doesn’t fit.
To transfer measurements from the scale model to the corresponding section on the mountain, a scale factor needs to be applied.
Scale factors can be used to create larger or smaller versions of an original. When creating the ratio, the first term represents the model or diagram measurement and the second term represents the actual (or object) measurement. A scale factor is a number without units.
The variable k is often used to represent an unknown scale factor.
— CANAVAN-MCGRATH ET AL. Principles of Mathematics 11,
© 2012 Nelson Education Limited. p. 467, 470. Reproduced by permission.
The following formulas are used to calculate scale factor. You may wish to add the following formulas to your Formula Sheet document.
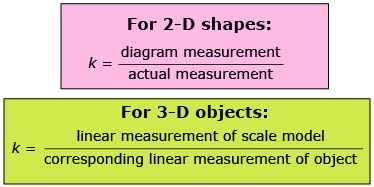
For instance, if measurements are taken off of the 1:300 scale model of Crazy Horse, each measurement would need to be multiplied by a scale factor of 300 to get the corresponding measurement for the mountain monument. This ensures that the mountain carving and the scale model are proportional, or similar objects.
Self-Check 1
1.2. Explore 2
Module 6: Proportional Reasoning
Whether an object is being enlarged or reduced, a scale factor ensures that the enlargement or reduction of an object is proportionally consistent with the original dimensions. In similar objects, the ratio of any two corresponding measurements or dimensions will be a constant number (i.e., the scale factor).
Read “Example 3: Determining scale factor” on page 470 of your textbook. Why is it important that both measurements be expressed in the same unit?
Choose one of the following options to explore examples involving the use of scale.
Option 1: In your favorite Internet search engine, type in “Ratio and Scale Absorb Learning.” The guided search should take you to the Absorb website with online courses. This resource will guide you through examples of how scale is used to create models and drawings.
Option 2: Use the Scale Factor applet to investigate how scale factor is used to produce proportional enlargements and reductions.
iStockphoto/Thinkstock
Self-Check 2
- Complete “Check Your Understanding” questions 1 and 2 on page 471 of your textbook. Answer
- Complete “Check Your Understanding” question 2 on page 490 of your textbook. Answer
Read “Example 1: Determining if two objects are similar” on page 484 of your textbook. How does Sandeep determine that the pans are proportional?
Self-Check 3
Complete “Check Your Understanding” question 1 on page 489 of your textbook. Answer
Try This 1
Go to the Internet and enter the keywords “Scale Factor X.” These keywords should take you to a website with a game, “Scale Factor X,” which allows you to practise your skills on proportion and scale factors. See if you can complete your mission before the Scaliens know you are there!
1.3. Lesson 4 Summary
Module 6: Proportional Reasoning
Lesson 4 Summary
In this lesson you investigated how diagrams and models can be used to represent 2-D shapes and 3-D objects. These diagrams allow sculptors and designers to produce an accurate representation of what their designs would look like on larger-than-life canvases, like a mountain, or smaller canvases, such as a coffee mug.
Scale models are proportional representations of 3-D objects. Scale diagrams are proportional representations of 2-D shapes. Designers use scale to produce accurate and proportional representations of objects and shapes. By relating the diagram or model’s measurement to the actual measurement, the scale factor can be determined.
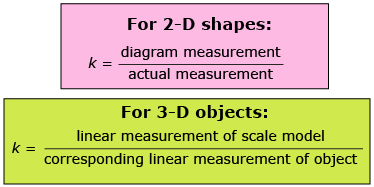
A scale factor of greater than 1 will result in an enlargement, while a scale factor between 0 and 1 results in a reduction. A scale factor of exactly 1 represents a full scale (1:1) model, which means that the dimensions stay the same.
In order for a diagram to be proportional to the original, all items on the diagram have to be drawn to the same scale. Likewise, in order for a model to be proportional to the original shape, all linear measurements need to be related by the same scale factor.
In Lesson 5 you will use scale diagrams and models to determine unknown dimensions.