Lesson 6
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-2 SS |
| Book: | Lesson 6 |
| Printed by: | Guest user |
| Date: | Tuesday, 30 December 2025, 7:25 AM |
Description
Created by IMSreader
1. Lesson 6
Module 6: Proportional Reasoning
Lesson 6: Scale Factors and Areas of 2-D Shapes
Focus

Have you ever noticed how some cartoon characters or figurines have heads that seem much bigger than the rest of their bodies? Bratz dolls, bobblehead dolls, and some cartoon characters, such as Betty Boop, are all examples of characters with heads that are not in proportion to the size of their bodies. Can you think of other examples of a character, doll, or figurine with a head that is oversized (or undersized) compared to the rest of its body?
In cartoons, large heads do not always mean the character has a large ego! The disproportionately large heads take up a larger area in the cartoon and make the characters stand out. Unlike cartoons, scale diagrams require dimensions and areas that are proportional. This ensures that the enlarged or reduced shapes are similar to the original ones.
This lesson will help you answer the following critical questions:
- When a shape is enlarged or reduced, what is the relationship between scale factor and a shape’s dimensions?
- When a shape is enlarged or reduced, what is the relationship between scale factor and a shape’s area?
Assessment
- Math Lab: Scale Factors and Areas of 2-D Shapes
All assessment items you encounter need to be placed in your course folder.
Materials and Equipment
- calculator
- ruler
There are companies that specialize in creating custom, personalized bobblehead dolls. You can get your own personal bobblehead cake topper or cellphone holder! Your bobblehead can even have its own motorbike, golf club, or furniture. How do you think the bobblehead creators ensure that the bobblehead looks like you? Is there a standard ratio between the size of the body and the size of the head that makes the figure a bobblehead?
1.2. Refresher
Module 6: Proportional Reasoning
Refresher
How did you do? Did you remember how to find the area of basic shapes? Great work, if you remembered! If you did not, carefully read this Refresher section.
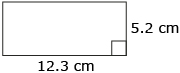
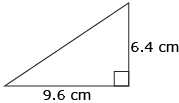
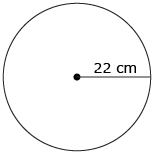
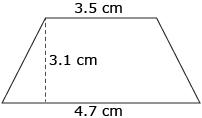
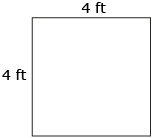
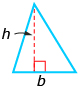
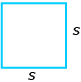
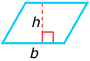
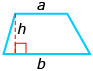
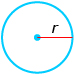
The following table shows the formulas for some basic shapes. If you haven’t done so already, you should add these to your formula sheet. You are not expected to memorize these formulas, but you do need to be familiar with them.
|
Area Formulas |
|
|
Shape |
Formula |
|
triangle
|
|
|
rectangle
|
|
|
square
|
|
|
parallelogram
|
|
|
trapezoid
|
|
|
circle
|
|
Adapted from: CANAVAN-MCGRATH ET AL. Principles of Mathematics 11,
© 2012 Nelson Education Limited. p. 475. Reproduced by permission.
The Mathematics Glossary defines the term area. The glossary contains an interactive Demonstration Applet and Flash animations to illustrate the definition.
Go to “Area Formulas.” This review of using formulas to find area for rectangles, squares, triangles, and parallelograms presents formulas solutions and some practice questions.
For additional review, you can also type the words “Math.com area of polygons and circles” into your favourite Internet search engine. You are looking for a website titled Math.com: The World of Math Online. You want Step 1: First Glance. There are a variety of resources available online to help you review and practice calculating the area of 2-D shapes.
1.3. Discover
Module 6: Proportional Reasoning
Discover

Comstock/Thinkstock
Kunal is not impressed with his new room in the basement of their new smaller house. He tells his sister Akuti that his old room is twice as big as his new one. Go to Kunal and Akuti’s Conversation to hear their conversation.
Let’s help Kunal figure out what the difference is.The following Math Lab will let you and Kunal figure out what the real size difference is between his old and new rooms.
Math Lab: Scale Factors and Areas of 2-D Shapes
Complete the Math Lab to learn how changing dimensions changes area. Once you complete the Math Lab, you will be issued a certificate of completion that you can hand in to your teacher for the assessment in this lesson.
1.5. Explore
Module 6: Proportional Reasoning
Explore
Does doubling the dimensions of an object double its area? Many people think it does. But as Kunal learned, this is not true! As you discovered in the Math Lab, when a scale factor (k) is applied to a 2-D shape, it creates a similar shape. The area of the similar shape (A2) is the product of the square of the scale factor (k2) and the area of the original shape (A1). We could write this as:
area of similar 2-D shape = k2 × area of the original shape
or
A2 = k2 × A1
Rearranging this formula allows you to determine the square of the scale factor that relates two similar 2-D shapes.
![]()
By taking the square root of the area of a shape divided by the area of the original shape, you can determine the scale factor.
![]()
You may find it helpful to go to the Formula Sheet document that you saved to your course folder and update the document with these formulas. Remember to save your updated Formula Sheet document to your course folder.
Self-Check 1
1.6. Connect
Module 6: Proportional Reasoning
Connect
If you haven’t done so already, submit your certificate of completion from Math Lab: Scale Factors and Areas of 2-D Shapes to your teacher for the assessment in this lesson.
Going Beyond
The activity “Fractured Pictures” allows you to generate interesting, irregular fractals. You start with a polygon and you input the number of sides. You then enter in a fractal scale factor. The program draws the figure by recreating a scaled copy of the original figure at each vertex. Give it a try! You can click on the link. Choose the “Learner” tab to see some example fractals that were created using the program.
1.7. Lesson 6 Summary
Module 6: Proportional Reasoning
Lesson 6 Summary
Unlike some cartoon characters, scale diagrams require dimensions and areas that are proportional. This ensures that the enlarged or reduced shapes are similar to the original ones. The dimensions of similar 2-D shapes are related by a scale factor.
A common misconception is that the area of two similar shapes is also related by the scale factor. But as you discovered in your Math Lab, the area of two similar shapes are related by the square of the scale factor (k2). The area of the similar shape is the product of the square of the scale factor (k2) and the area of the original shape.
area of similar 2-D shape = k2 (area of original shape)
You can rearrange this formula to isolate the square of the scale factor that relates the two similar 2-D shapes.
![]()
The scale factor can be determined by taking the square root of the area of a shape divided by the area of the original shape.
![]()
In Lesson 7 you will investigate the relationship between the scale factor and the surface area of two similar 3-D objects and the relationship between the scale factor and the volumes of two similar objects.