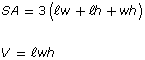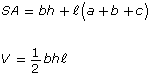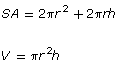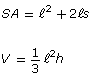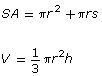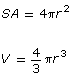Lesson 7
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-2 SS |
| Book: | Lesson 7 |
| Printed by: | Guest user |
| Date: | Tuesday, 30 December 2025, 7:27 AM |
Description
Created by IMSreader
1. Lesson 7
Module 6: Proportional Reasoning
Lesson 7: Scale Factors and 3-D Objects
Focus
Moving can sometimes involve long road trips. Some passengers take this time to read, play games, or solve puzzles. One popular road-trip puzzle is the Rubik’s Cube.
The Rubik’s Cube is a six-sided 3-D puzzle. Each side of the original game includes 3 × 3 small cubes of the same colour. The objective of the game is to twist and turn the small cubes until the colours on each side are all mixed up, and then to twist and turn again until the colours are in their original state—one colour per side of the cube.
There are many versions of the original puzzle, including the Rubik’s Mini Cube, which is a 2 × 2 cube puzzle, and Rubik’s Revenge, a 4 × 4 cube with some special features that make the puzzle even harder to solve.
The 5 × 5 Rubik’s Professor’s Cube might be the toughest of the games. It has been calculated that there are 282 870 942 277 741 856 536 180 333 107 150 328 293 127 731 985 672 134 721 536 000 000 000 000 000 possible arrangements of the Professor’s Cube!
This lesson will help you answer the following critical questions:
- When a 3-D object is enlarged or reduced, what is the relationship between scale factor and the object’s surface area?
- When a 3-D object is enlarged or reduced, what is the relationship between scale factor and the object’s volume?
Assessment
- Math Lab: Scale Factors and Areas and Volumes of 3-D Objects
All assessment items you encounter need to be placed in your course folder.
Materials and Equipment
- calculator
- ruler
1.1. Are You Ready?
Module 6: Proportional Reasoning
Are You Ready?
- What makes a prism different from a pyramid? Answer
- Look at the 3-D objects in the illustration. Identify whether each one is a prism or a pyramid.
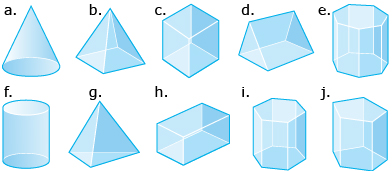
Answer
- Determine the surface area of the following pyramid to the nearest square inch.
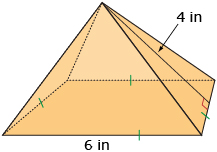
Answer
- Determine the surface area of the cylinder to the nearest square centimetre.
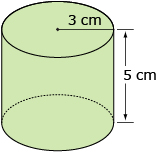
Answer
- Determine the surface area of the following prism, rounded to the nearest square centimetre.
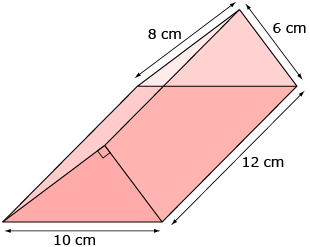
Answer
- Consider the net shown. What does this net represent?
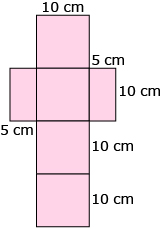
- A cube with a side 10 cm.
- A box with a length and width of 10 cm and a height of 5 cm.
- A box with a length and width of 5 cm and a height of 10 cm.
- This net does not represent a box.
- A cube with a side 10 cm.
- Find the surface area of the following sphere to the nearest square metre.
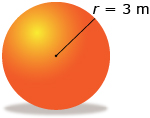
Answer
- Determine the radius of a sphere with a surface area of 64π cm2. Report your answer to the nearest centimetre. Answer
- Determine the surface area of the following cone to the nearest square foot.
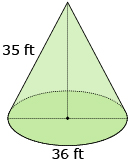
Answer
- What are some differences between area and volume? Answer
- What is the formula for the volume of a rectangular prism? Answer
- Find the volume of a rectangular prism with a length of 14 m, a width of 3 m, and a height of 2 m. Answer
- How could you find the volume of a 3-D object without multiplying or using a formula? Answer
- Find the volume of the triangular prism shown here.
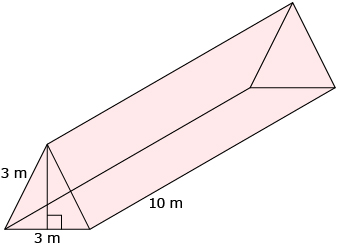
Answer
- Find the volume of the square pyramid shown in the diagram.
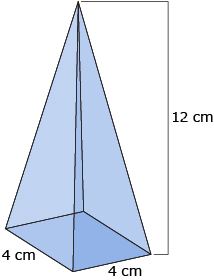
Answer
1.2. Refresher
Module 6: Proportional Reasoning
Refresher
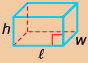
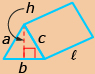
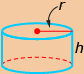
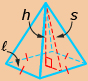
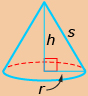
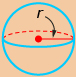
The formulas for determining the surface area and volume of some 3-D objects are shown in the following table.
|
Formulas |
|
|
Object |
Surface Area and Volume |
|
rectangular prism
|
|
|
right triangular prism
|
|
|
right cylinder
|
|
|
right pyramid
|
|
|
right cone
|
|
|
sphere
|
|
Source: CANAVAN-MCGRATH ET AL. Principles of Mathematics 11, © 2012 Nelson Education
Limited. p. 495. Reproduced by permission.
You may find it helpful to add these formulas to the Formula Sheet document that you saved to your course folder. Remember to save your updated Formula Sheet document to your course folder.
If you feel you need more of a refresher on calculating surface area and volume of 3-D objects, you can refer to Math 10C Learn EveryWare: Module 1: Lesson 4 (Surface Area of 3-D Objects) and Math 10C Learn EveryWare: Module 1: Lesson 5 (The Volume of 3-D Objects). These courses can be accessed through the T4T tab on LearnAlberta.ca. You will need your school’s LearnAlberta username and password to access these resources. If you don’t know these, contact your teacher.
Additional resources on calculating surface area and volume of 3-D objects can be found by doing an Internet search using keywords such as “surface area of 3-D objects” and “volume of 3-D objects.” Interactive animations help you to visualize and calculate surface area and volume of 3-D objects.
1.3. Discover
Module 6: Proportional Reasoning
Discover

Polka Dot/Thinkstock
There are 27 individual cubes in the original 3 × 3 Rubik’s Cube. These “cubelets” or “cubies” are similar to the Rubik’s Cube itself. The scale factor between the length of a side of a cubelet and the length of a side on the Rubik’s Cube is 3.
The 4 × 4 Rubik’s Revenge is made up of 56 small cubes. The scale factor between the length of a side of a cubelet and the length of a side on the 4 × 4 cube is 4. The 5 × 5 Rubik’s Professor’s Cube contains 98 cubelets. If the smaller cubelets and the larger cubes are similar, what do you think the scale factor is between the dimensions of the cubelets and the dimensions of the 5 × 5 cube? That’s right—it’s 5!
As you know, each cube is made up of similar, smaller cubes. What do you think the relationship is between the scale factor and the surface areas of these two similar objects? What about the relationship between the scale factor and the volumes of the original cube and the cubelets? If there is a relationship, do you think it applies to other 3-D objects such as rectangular prisms, right cylinders, or cones?
Math Lab: Scale Factors and Areas and Volumes of 3-D Objects
This Math Lab will help you answer the questions from the Discover section. Once you complete the Math Lab, you will be issued a certificate of completion that you can hand in to your teacher for the assessment in this lesson.
1.4. Lesson 7 Summary
Module 6: Proportional Reasoning
Lesson 7 Summary
You started this lesson by looking at the different versions of the Rubik’s Cube. (For more review about the Rubik’s Cube, you can turn to page 506 of the textbook.)
In Math Lab you gathered evidence that further supported the relationships between the surface area and volume of similar 3-D objects. You discovered that the surface area of a similar object is related to the original object by the square of the scale factor (k2). The volume of a similar object is related to the volume of the original object by the cube of the scale factor (k3). These relationships can be stated as shown.
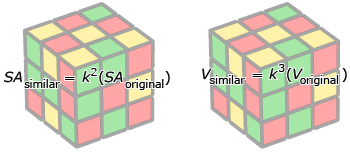
If you know the surface areas or volumes of two similar objects, you can determine the scale factor that relates their dimensions. The scale factor is the square root of the ratio of the surface areas, or the cube root of the ratio of the volumes, of the two similar objects.
In Lesson 8 you will use the relationships you have identified to solve problems involving scale factor and 2-D shapes or 3-D objects.