Lesson 8
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-2 SS |
| Book: | Lesson 8 |
| Printed by: | Guest user |
| Date: | Tuesday, 30 December 2025, 9:24 AM |
Description
Created by IMSreader
1. Lesson 8
Module 6: Proportional Reasoning
Lesson 8: Solving Spatial Problems
Focus

Brand X Pictures/Thinkstock
Moving from one home to another is a complicated process requiring organization and planning. Imagine that you need to move: You need to determine how to get all your stuff from your old location to your new location. Then you have to figure out whether it all fits in your new place. This involves spatial reasoning.
Planning for a move might involve estimating how many and what size of boxes you will need to pack up all your belongings. You then have to determine how you are going to get it all there. Will the belongings all fit in the back of a few pick-up trucks? Or will you need to rent a larger moving van? Maybe you decide to hire professional movers with a semi-trailer.
Packing requires a clear plan of attack. How can you arrange the boxes and furniture so that you have to do the least number of loads? You also need to take into account the capacity and weight of each box. Your friends will never help you move again if you make the boxes so heavy no one can lift them!
Once you get to your new place, the unpacking begins. You have to find places for all your stuff, including your furniture.
In this lesson you will use your understanding of scale factor, area, and volume to solve problems involving 2-D objects and 3-D shapes.
This lesson will help you answer the following critical question:
- How can the relationships among scale factors, areas, and volumes be used to solve problems?
Assessment
- Lesson 8 Assignment
- Module 6 Project: Part 3
All assessment items you encounter need to be placed in your course folder.
Save a copy of the Lesson 8 Assignment to your course folder. You will receive more information about how to complete the assignment later in this lesson.
In this lesson you will also be directed to work on Part 3 of the Module 6 Project.
Materials and Equipment
- calculator
- ruler
1.1. Explore
Module 6: Proportional Reasoning
Explore
The process of moving involves a lot of “making sure things fit.”

Comstock/Thinkstock
Akuti has decided to decorate one of the walls in her new room with a mural. The wall is 11 ft long by 8 ft high. Akuti wants the mural to be centred on the wall and has decided to make it a similar rectangle to the wall with a scale factor of 1:2.
Try This 1
Use the interactive animation Drawing a Mural to help Akuti determine the area and placement of the mural on her bedroom wall.
Did You Know?
Murals can be found all over Alberta. Some towns like Trochu, Three Hills, and High River have murals painted on the outside of buildings. The artists need to ensure that the images on the murals are proportional. Can you find other examples of murals in your community?

© Travel Alberta
The strategy Akuti used to determine the area of her mural is only one way of solving the problem. Equations can also be used to solve for the unknown area.
Read “Example 1: Reasoning about scale factor and area” on pages 476 and 477 of the textbook. Jasmine and Hank used different strategies to determine the actual area. As you read over the example, think about why the value of k is greater than 1 in Jasmine’s solution but less than 1 in Hank’s solution.
The relationship between area and scale factor of two similar objects can also be used to determine dimensions.
Read “Example 2: Reasoning about scale factor and area to determine dimensions” on pages 477 and 478 of the textbook. As you look at Rani’s solution, consider the following questions:
- How did Rani know that the rectangles were similar?
- Why did Rani need to determine the square root of k2?
Self-Check 1
- Complete “Your Turn” on page 478 of your textbook. Answer
- Complete “Practising” questions 6, 7, 9, 10, and 15 on pages 480 and 481 of your textbook. For question 15, the measurements of the rectangle are 2.6 cm by 0.75 cm. Answer
- If you want a challenge, try “Extending” questions 18 and 19 on page 482 of your textbook. Answer
1.2. Explore 2
Module 6: Proportional Reasoning

Comstock/Thinkstock
Hemera/Thinkstock
A large part of the moving process is figuring out whether things will fit in the new home. This also applies to the unpacking stage. For instance, moving into a new house will likely require a new arrangement of existing furniture or it may even require buying new furniture that fits properly in the new location.
Rajesh is responsible for setting up the family’s entertainment unit in the downstairs living room. The family ordered a new 52 in LCD panel TV to go in their old entertainment unit. The entertainment unit is modular and can be arranged in a variety of different ways.
Try This 2
Use the applet Assembling a TV Cabinet to help Rajesh determine what size of opening he needs for the TV in the entertainment unit.
1.3. Explore 3
Module 6: Proportional Reasoning
There are several strategies that Rajesh could have used to determine what size of opening he needs for the TV in the entertainment unit. Three possible strategies follow.
| Strategy 1 | Strategy 2 | Strategy 3 |
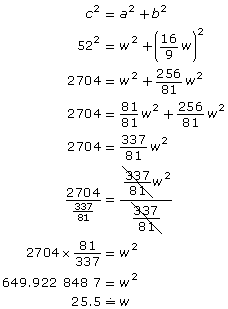 |
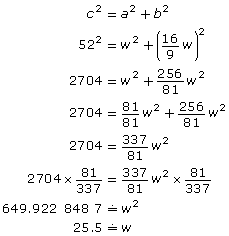 |
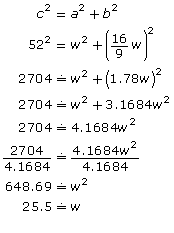 |
Self-Check 2
1.4. Explore 4
Module 6: Proportional Reasoning
In Lesson 7 you made conjectures about the relationships among scale factor, surface area, and volume.
Turn to page 496 of the textbook and read “Connor’s Solution: Proving the conjecture for surface area” to see a proof of the surface area conjecture. (Connor’s solution appears in the first section of “Example 1: Reasoning about relationships among scale factor, surface area, and volume.”)
The relationships among surface area and volume of similar 3-D objects can be used to solve problems.
Read “Example 2: Solving a surface area problem” on pages 497 and 498 of the textbook to see how the relationship between scale factor and surface area can be used to determine how much glass is needed to create a replica of the Great Pyramid of Giza.

Hemera/Thinkstock
Did You Know?
The Great Pyramid of Giza is the largest pyramid ever built. It incorporates about 2.3 million stone blocks. The stone blocks weigh an average of 2.5 to 15 tons each! It is estimated that the workers would have had to set a stone block every 2.5 minutes.1
1 © National Geographic Society. Reproduced with permission.
For more information on the pyramids, search for “Egypt pyramids facts” using an Internet search engine.
Self-Check 3
Complete “Your Turn” on page 498 of your textbook. Answer
Return to pages 496 and 497 of the textbook and read “Isabel’s Solution: Proving the conjecture for volume” to see a proof of the volume conjectures you made in the last lesson. (Isabel’s solution appears in the second section of “Example 1: Reasoning about relationships among scale factor, surface area, and volume.”)
1.5. Explore 5
Module 6: Proportional Reasoning
Did You Know?
Algarrobo, Chile claims to be home to the world’s largest swimming pool. The San Alfonso del Mar pool, which was constructed in 2006, is 1012 m long.
A common misconception is that volume and capacity are the same when, in fact, they are not. Volume is the amount of space that is occupied by an object. Capacity is the amount that a container holds. So the volume of a swimming pool is the amount of space the entire pool takes up (including the walls) while the capacity of a swimming pool is the amount of water it holds.

Comstock/Thinkstock
Rajesh, Kunal, and Akuti’s new neighbors, the Jones family, are building an in-ground pool and hot tub in their backyard. Once the pool was dug, Mr. Jones decided that it just wasn’t big enough. He told the contractor to make the whole thing 25% larger.
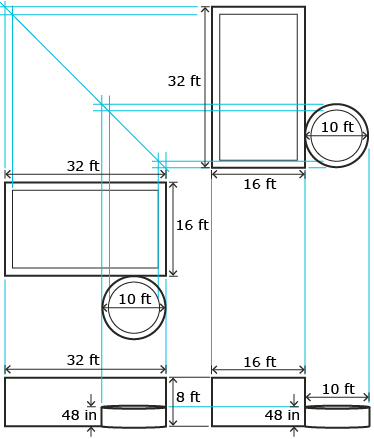
Try This 3
Mr. Jones didn’t specify to the contractor what was to be 25% larger: the dimensions, the surface area, or the volume of the pool. Use the applet Scaling Up a Pool to determine the difference between increasing the dimensions of the pool by 25%, increasing the area of the pool by 25%, or increasing the volume of the pool by 25%.
water: Hemera Technologies/AbleStock.com/Thinkstock;
characters: iStockphoto/Thinkstock
Share 1
Work with a partner to determine the new dimensions of the hot tub when the dimensions are increased by 25%, the area is increased by 25%, and the volume in increased by 25%. Assume that the hot tub is shaped like a right cylinder. Go back and look at Scaling Up a Pool if you are having trouble.
1.6. Explore 6
Module 6: Proportional Reasoning
In Try This 3 and Share 1 you found out that making a pool and hot tub 25% larger could result in different dimensions depending on whether the dimensions are increased by 25%, the area is increased by 25%, or the volume is increased by 25%.
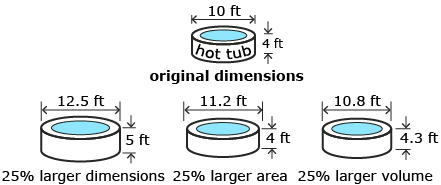
Did you and your partner determine the same new dimensions for making the hot tub 25% larger? If not, compare your answers with the Share 1 Solutions.
Self-Check 4
- Complete “Check Your Understanding” question 2 on page 500 of the textbook. Answer
- Complete “Practising” questions 5, 7, 10, 11, and 14 on pages 501 and 502 of the textbook. Answer
- Complete “Extending” question 20 on page 503 of the textbook. Answer
This is the last lesson in this module. As you have been progressing through each lesson, you have been adding to your Glossary Terms document and your notes organizer. At this point, you may find it helpful to refer to the following items in Chapter 8 of your textbook.
- “In Summary” boxes at the end of each section in the textbook
- “Mid-Chapter Review” on pages 463 and 464 of the textbook
- “Chapter Review” on pages 505 and 506 of the textbook
It would be useful to review these concepts as you prepare to complete this module.
1.7. Connect
Module 6: Proportional Reasoning
Connect
Lesson Assignment
Complete the Lesson 8 Assignment that you saved to your course folder.
Project Connection
You are now ready to complete the rest of the project for this module. Open the Module 6 Project and refer to the instructions in Part 3 of the project.
1.8. Lesson 8 Summary
Module 6: Proportional Reasoning
Lesson 8 Summary

adapted from: iStockphoto/Thinkstock
The process of moving involves a lot of “making sure things fit.” In this lesson you used your understanding of scale factor, area, and volume to solve problems involving 2-D objects and 3-D shapes. You helped Akuti work with scale factors to place her mural in the right place on her wall and make it the correct size. Rajesh needed assistance in making sure his new TV would fit in his entertainment centre before he assembled it.
When trying to determine how dimensions of a 3-D object change with an increase or decrease by a certain factor, an understanding of the relationships among scale factors, area, and volumes is required. In the pool example, you used these relationships to show Mr. Jones that making a 3-D object “25% larger” can mean several things.
You have used proportional reasoning to solve a wide variety of problems in this module. Refer to the Module 6 Summary for an overview of concepts you investigated in this module.