Lesson 2
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-1 SS |
| Book: | Lesson 2 |
| Printed by: | Guest user |
| Date: | Thursday, 4 December 2025, 2:12 AM |
Description
Created by IMSreader
1. Lesson 2
Module 1: Sequences and Series
Lesson 2: Applications of Arithmetic Sequences
Focus

liquidlibrary/Thinkstock
Wouldn’t it be nice to have a money tree? Just plant a penny, water regularly, and watch the tree grow. After a season you could harvest the riches! While you may not have a money tree, you can still grow your money by investing your dollars.
If you are just starting to invest, you might deposit your money into a savings account. You could also buy guaranteed investment certificates or savings bonds. By taking any of these actions, you will earn interest on your money.
Interest is the rate of return that a bank pays you for saving money. The amount you earn depends on several factors, including how much you save, how long you leave your money in the bank, and the interest rate your money earns.
In this lesson you will continue your study of arithmetic sequences. You will discover a relationship between arithmetic sequences and linear functions, a topic you studied in a previous math course. You will also use arithmetic sequences to model and solve a variety of problems.
Outcomes
At the end of this lesson you will be able to
- describe the relationship between arithmetic sequences and linear functions
- solve a problem that involves an arithmetic sequence
Lesson Questions
In this lesson you will investigate the following questions:
- How are arithmetic sequences related to linear functions?
- How are sequences useful in solving problems?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 2 Assignment (Download the Lesson 2 Assignment and save it in your course folder now.)
- course folder submissions from Math Lab, Try This, and Share activities
- additions to Module 1 Glossary Terms and Formula Sheet
- work under Project Connection
Materials and Equipment
You will need a ruler and a pencil.
1.1. Launch
Module 1: Sequences and Series
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? Launch will help you find out.
1.2. Are You Ready?
Module 1: Sequences and Series
Are You Ready?
Complete these questions. If you need help, visit Refresher or contact your instructor.
- For each of the following arithmetic sequences, use the general term tn = a + (n − 1)d to find the indicated variable.
- What is a linear function? Answer
- State what a linear function looks like when the linear function is expressed in each of the following ways:
- For each of the following linear-function graphs, write the corresponding equation.
- State the domain for each of the following graphs:
1.3. Refresher
Module 1: Sequences and Series
Refresher
In Lesson 1 you examined arithmetic sequences. You used specific terms, such as common difference and general term, to describe the properties of these sequences.
Go to page 9 of the textbook to refresh your memory about arithmetic sequences and how you can use the general term to identify the properties of these sequences.
Reread “Example 1” and then try “Your Turn” on pages 10 to 11 of the textbook. If you have any questions, contact your teacher. Answer
Use Graphing and Analyzing Equations to review the properties of linear functions. Select “Linear Functions,” and then select “Graphing and Analyzing Equations.” In the first slide, see if you can discover a definition for linear function. Then work through slides 1 to 7. Focus on how a linear function is represented in a table and in a graph.
Now watch Determining the Equation of a Line: Given the Graph. This interactive lesson will review how you can determine the equation of a line in slope-intercept form when given information from a graph.
The domain of a relation consists of all values of the independent variable. The range of a relation consists of all values of the dependent variable. Use Domain and Range to check your knowledge of domain and range.
Work through the following pages: (1) Domain and Range
(2)
Domain and Range from Graphs
Use Percent to review concepts relating to percentage. In the first topic you will review the definition of percent. In the second topic you will practise determining equivalent percents, fractions, and decimals. In the final topic, you will have the opportunity to play a game that tests not only your knowledge of percents, but also your reflexes! To begin, select “Percent (Food)” under the “Number” column, and then start with the first topic.
Go back to the Are You Ready? questions and try them again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 1: Sequences and Series
Discover

© foto76/24001220/Fotolia
Look at the unfurling fern tip in the photo. How would you describe the fern tip's shape? The spiral is found everywhere in nature. Besides the shape of fern tendrils, the spiral is also found in these places in the animal kingdom: a giraffe's intestine, a centipede's death pose, and a butterfly's tongue.
How do spirals relate to arithmetic sequences? Prepare to find out in the following Math Lab. You will investigate Archimedes' Spiral, one of the simplest spiral forms.
Problem Question
How are arithmetic sequences related to linear functions?
Materials
You will need
- a ruler
- Archimedes' Spiral Template
- a pencil
Hypothesis
Form a hypothesis to answer the problem question. Do you remember what a hypothesis is? ![]()
Procedure
Step 1: Print a copy of Archimedes' Spiral Template, provided in the Materials list.

Step 2: Identify the points along the spiral that intersect the radii (or spokes) of the circle. Mark these with small dots.

Step 3: Use your ruler to measure the length from the centre to the first point of intersection with a spoke as you wind from the centre to the outer edge. Repeat for each intersection point as you continue from the centre and radiate outward. Once you have 12 data values, record your measurements to the nearest millimetre in a table like this one. Then proceed to Analysis.
Radius |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Distance to Intersection |
Analysis
- Study your measurements. What kind of sequence do your measurements form? What is the common difference?
-
- Determine an expression of the form tn = a + (n − 1)d for the sequence. Simplify the expression.
- What does n represent in this expression?
- What does tn represent in this expression?
- Does the simplified form of the expression remind you of any other expression?
- Determine an expression of the form tn = a + (n − 1)d for the sequence. Simplify the expression.
- Plot a graph showing tn versus n.
- Do you think the points should be connected? Why or why not?
- Describe the type of function that is represented by the graph?
- What property of the sequence corresponds to the slope of the graph?
How do your results compare to your initial hypothesis?
![]() Save your results in your course folder.
Save your results in your course folder.
You will use your results again later in the lesson.
1.5. Explore
Module 1: Sequences and Series
Explore

© 2011 Jupiterimages Corporation
When you invest, your money is in turn invested by the bank or investment company. In other words, your money is used to earn money. As a result, you are entitled to a portion of the increase. The portion that you receive is called interest.
The interest you receive is often a percentage of the amount you invest. The more money you invest, the more interest you earn. Simple interest is earned when you earn interest as a percentage of the original investment year after year. If you invest $800 and earn 5% per year, how much simple interest can you expect to receive each year?
In Try This 1 you will see how earning simple interest can be viewed as an example of both an arithmetic sequence and a linear function. You will also investigate how arithmetic sequences are related to linear functions.
You already saved Module 1 Glossary Terms in your course folder. In this lesson you will define these terms, and maybe others, in your copy of Module 1 Glossary Terms:
- linear function
- simple interest
Try This 1

Digital Vision/Thinktock
Imagine that you are investing $1000 in a savings bond that pays 4% simple interest at the end of every year.
- Calculate the simple interest you would earn each year.

- Complete a table like this one.
Year
1 2 3 4 5 6 Total Value of Investment ($) at End of Each Year
1040 1080 
- Graph the year versus the value of the investment.
- Use the graph to find the total value of the investment after 10 years.
- After how many years will the total value of the investment be equal to $1480?
![]() Save a copy of your answers in your course folder.
Save a copy of your answers in your course folder.
Share 1
Discuss your results with a classmate or in a group. In your discussion, address the following points:
- How does this situation represent an arithmetic sequence? How does the situation represent a linear function?
- Is the graph more accurately represented with or without a line drawn through the points? Give reasons to support your answer.
![]() If required by your teacher, save notes from your discussion in your course folder.
If required by your teacher, save notes from your discussion in your course folder.
1.6. Explore 2
Module 1: Sequences and Series
Arithmetic Sequences and Linear Functions
In Try This 1 you saw how investments earning simple interest follow an arithmetic progression that can be expressed in the form tn = a + (n − 1)d. You then represented this as a linear function.
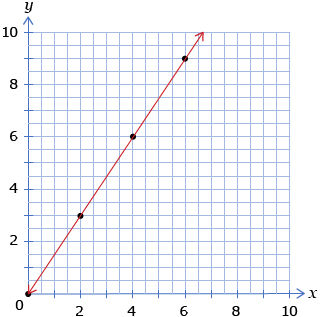
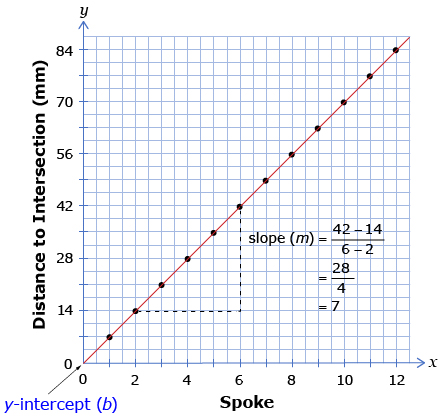
In the Math Lab, you investigated arithmetic progressions based on an Archimedes' Spiral. You may have discovered that the points of intersection with each spoke of the spiral follow an arithmetic progression that can also be expressed in the form tn = a + (n − 1)d. You then plotted a graph showing tn versus n. Retrieve this graph from your course folder. Compare your graph to Figure 1.
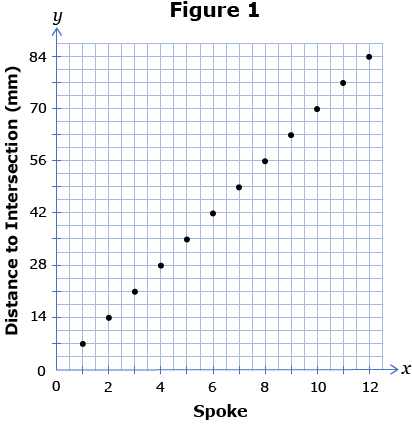
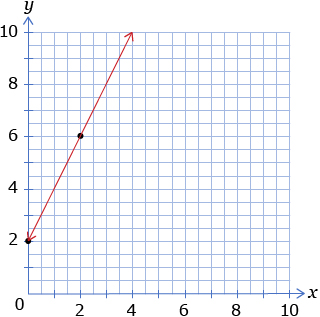
Your graph should also show 12 points positioned along a diagonal. Would it be more or less appropriate to sketch the graph as shown in Figure 2?
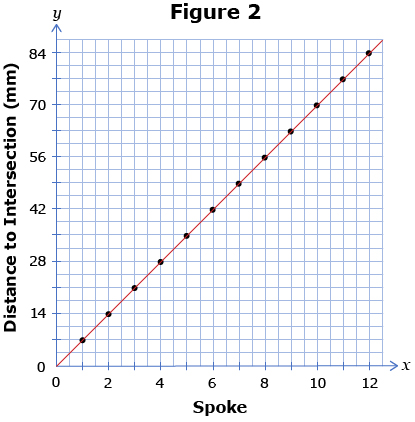
Notice that, in Figure 2, a line is drawn through the points. If a graph is drawn in this way, it is implied that every point on the graph is valid, even the points that occur between the points marked in black.
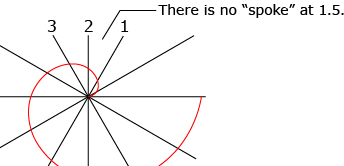
There are many points on the graph that do not have meaning in the context of Archimedes' Spiral. For example, the point (1.5, 10.5) is on the line but has no meaning in the context of the investigation, since there is no spoke between the first and second spoke!
Recall from your previous math studies that the equation of a linear function is given by the form f(x) = mx + b. You can use this formula to determine the equation of the line representing the Archimedes' Spiral.
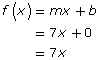
1.7. Explore 3
Module 1: Sequences and Series
Arithmetic Sequences Described by Linear Functions
As you can see, arithmetic sequences can be described by linear functions.
 Watch Direct and Partial Variation: Arithmetic Sequences to further visualize the connection between arithmetic sequences and linear functions. You will see how the general term of an arithmetic sequence is related to the equation of a line.
Watch Direct and Partial Variation: Arithmetic Sequences to further visualize the connection between arithmetic sequences and linear functions. You will see how the general term of an arithmetic sequence is related to the equation of a line.
If you have trouble viewing this video, make sure you have downloaded the necessary software from the LearnAlberta website. For example, you will need the latest version of Java and the APM reader.
From your work in this lesson, you should have discovered that an arithmetic sequence can be defined as a linear function whose domain consists of natural numbers. ![]()
 You may have noticed that the equation of a linear function corresponds to the general-term expression of an arithmetic sequence. Use Arithmetic Sequences Versus Linear Functions to confirm your understanding of the relationship between an arithmetic sequence and a linear function.
You may have noticed that the equation of a linear function corresponds to the general-term expression of an arithmetic sequence. Use Arithmetic Sequences Versus Linear Functions to confirm your understanding of the relationship between an arithmetic sequence and a linear function.Go to pages 14 to 15 of the textbook and work through “Example 4,” which demonstrates the relationship between an arithmetic sequence and a linear function. Read the problem and focus on the wording. Then read the solutions with particular focus on “Method 2: Use a Graph.” As you read, look for answers to the following questions:
- What is the significance of the phrase “plus $42/hr or portion of an hour”?
- When is it appropriate to model a problem using an arithmetic sequence?
- What property of the graph corresponds to the common difference of the arithmetic sequence?
Self-Check 1
Check your understanding of arithmetic sequences by completing Arithmetic Sequences Quiz.
1.8. Explore 4
Module 1: Sequences and Series
Example: Part-Time Job
Now that you have studied the relationship between arithmetic sequences and linear terms, you are ready to investigate the application of these principles in a problem-solving context. Work through Part-Time Job. See how you can use both sequences and linear functions to solve a problem related to earning income.
Throughout this interactive example you will be given a chance to try each step before you see the answer. Once you have tried a step, select the Check button to compare your solution to the solution provided in the example.
In Part-Time Job you should have discovered that you can use the properties of linear functions to set up and solve an arithmetic-sequence problem. Conversely, you can also use an arithmetic sequence to solve a problem involving linear functions!
Try This 2

Photodisc/Thinkstock
Use the photo shown to respond to the following questions.
- What is the significance of a staircase made of money?
- What part of the lesson does the photo remind you of?
- What is the connection between steps in a staircase and arithmetic sequences?
- What other analogies can you think of that could be used to describe arithmetic sequences? You may wish to describe your thoughts in paragraph-form or to find a photo that represents your analogy.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 2
Share your responses to Try This 2 question 4 with a partner or group. Create a combined list of analogies used to describe arithmetic sequences.
![]() Save a copy of this list in your course folder. You will need this list to complete the Lesson 2 Assignment.
Save a copy of this list in your course folder. You will need this list to complete the Lesson 2 Assignment.
Self-Check 2
Complete questions 7, 13, 16, 17, and 19 on pages 17 to 19 of the textbook. Show your work to support your answers. You may find you need to review relevant parts of this lesson as you work through the problems. Answer
1.9. Connect
Module 1: Sequences and Series
Open the Lesson 2 Assignment you saved in your course folder at the start of this lesson. Print one sheet of Polar Grid Paper. Complete the assignment.
Project Connection
In Module 1 Project: Financing Your Dreams, complete Project Connection 2: Budgeting.
![]() Save all of your work in your course folder. You will build on your work in each lesson.
Save all of your work in your course folder. You will build on your work in each lesson.
Going Beyond

© bofotolux/18870189/Fotolia
You have already seen arithmetic sequences applied in several different real-world contexts. These contexts include simple interest, Archimedes' Spiral, and auditorium seating. In fact, you can model situations using an arithmetic sequence whenever you discover a pattern of repetitive addition.
You will now investigate perpetual calendars, another application of arithmetic sequences. Can you figure out what the common difference is when an arithmetic sequence is used to model a calendar?
Part A
- Find a calendar for the current year. For the first two months of the calendar year, construct a table that shows which days of the year fall on a Thursday. Your table might look like the following:
Thursday Day of the Year 1st 3 2nd 10 3rd 4th 5th 6th 7th 8th
- Graph the data from the table. Show the independent values (left-column data) on the horizontal axis and the dependent values (right-column data) on the vertical axis.
- Determine the general term, tn, that relates the day of the year to the Thursday position.
Part B
Check the Internet to learn more about perpetual calendars. Try these questions to help you begin your investigation:
- If January 1 occurs on a Thursday this year, what day of the week will January 1 land on next year? Does the answer depend on any other factors?
- When do leap years occur? How can you determine if a particular year is a leap year?
- How many one-year calendars does a perpetual calendar consist of?
- What are the steps used to calculate the day of the week for a particular date?
- What are each of the World Calendar, the International Fixed Calendar, and the Pax Calendar?
Your search might lead to other questions.
![]() Save your work in your course folder.
Save your work in your course folder.
1.10. Lesson 2 Summary
Module 1: Sequences and Series
Lesson 2 Summary

© sculpies/17156309/Fotolia
In this lesson you investigated the following questions:
- How are arithmetic sequences related to linear functions?
- How are sequences useful in solving problems?
You continued your study of arithmetic sequences. You investigated how arithmetic sequences are related to linear functions. By investigating the properties of an Archimedes' Spiral you found that arithmetic sequences are linear functions whose domains are restricted to natural numbers.
As a result, the graph comparing the term value to the position of the term is linear. Connecting the points in these graphs is inappropriate since points along the graph that are between two consecutive terms are meaningless.
You also analyzed situations that can be modelled by arithmetic sequences. You practised using arithmetic sequences to solve problems involving part-time earnings and investing for simple interest. You studied patterns and constructed tables and graphs to develop equations and formulas that described the context.
You learned that such contexts can be described by the linear equation y = mx + b and by the general term tn = a + (n − 1)d. You used those formulas and equations to solve other problems. By summarizing a pattern in the form of an equation, you can predict future behaviour.
In the next lesson you will continue your study of sequences by focusing on adding the terms of an arithmetic sequence.