Lesson 3
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-1 SS |
| Book: | Lesson 3 |
| Printed by: | Guest user |
| Date: | Thursday, 4 December 2025, 2:08 AM |
Description
Created by IMSreader
1. Lesson 3
Module 1: Sequences and Series
Lesson 3: Arithmetic Series
Focus
Ever consider a career working in finance? Jobs in the finance industry involve working with money. You may know people who work with money, such as cashiers and bank tellers. However, many finance jobs do not involve actually handling bills and coins. In fact, most of the jobs in the finance industry help people or companies manage their money and make good decisions about how to spend or save their money.

© Alexander Raths/20754137/Fotolia
You may think of accounting, financial counseling, or investment banking when discussing occupations related to finance, but there are many more occupations available that are both interesting and fulfilling. For example, you could be an appraiser, controller, or risk manager.
Before you get started on this lesson you may want to search the Internet to find out more about these jobs. Whatever job you accept, whether or not it's in the finance industry, you will want to know how much you get paid and how often you can expect to get a raise.
Some employees earn wages and others are salaried. Employers pay their employees biweekly, monthly, or as individual assignments are completed. For many companies, raises are applied at regular intervals; in other situations, raises may come infrequently and be based on performance.
In this lesson you will look for patterns that occur when the terms of an arithmetic sequence are added together. You will develop and learn to use methods and formulas to find sums efficiently.
Outcomes
At the end of this lesson you will be able to
- derive a rule for determining the sum of n terms of an arithmetic series
- determine t1, d, n, or Sn in a problem that involves an arithmetic series
- solve a problem that involves an arithmetic series
Lesson Questions
You will investigate the following questions:
- How are arithmetic sequences and arithmetic series similar and different?
- How can you visualize the sum of an arithmetic series?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 3 Assignment (Download the Lesson 3 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Module 1 Glossary Terms and Formula Sheet
- work under Project Connection
Materials and Equipment
You will need scissors.
1.1. Launch
Module 1: Sequences and Series
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? Launch will help you find out.
1.2. Are You Ready?
Module 1: Sequences and Series
Are You Ready?
Complete these questions. If you experience difficulty and need help, visit Refresher or contact your teacher.
- What is an arithmetic sequence? Answer
- Consider the arithmetic sequence 17, 21, 25, 29, ….
Determine the following values.
- Rearrange the general term tn = a + (n − 1)d for each of the following variables.
- What is a system of equations? Answer
- Solve the following system of equations.
How did the questions go? Depending on your answer, skip forward to Discover or work through Refresher.
1.3. Refresher
Module 1: Sequences and Series
Refresher
In the video Direct and Partial Variation: Arithmetic Sequences you will encounter the terms direct variation and partial variation. You are not required to know what these terms mean. However, in order to easily follow along, you should know that
- any linear function with a y-intercept of zero exhibits direct variation
- any linear function with a non-zero y-intercept exhibits partial variation
Search the Internet if you would like more information on direct variation and partial variation.
Watch Direct and Partial Variation: Arithmetic Sequences. Work through slides 1 to 11. You will review
-
the basic properties of arithmetic sequences
- the relationship between arithmetic sequences and linear functions
For the next two review pieces, click on “Solving Linear Systems Algebraically” after you click on each play button below. Then click on the “Tutorial” button at the top of the applet. You will then be able to select each of the topics listed here:
- Solving Linear Systems Algebraically: Substitution
- Solving Linear Systems Algebraically: Elimination
Once you have completed the tutorial, select “Example” at the top of the applet in order to try some guided questions.
To further review solving linear systems algebraically, work through Module 7, Lessons 3 and 4 in Mathematics 10C Learn Everywhere.
Go back to the Are You Ready? questions and try them again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 1: Sequences and Series
Discover
Try This 1
Look at the photos showing different human pyramids.

A: Comstock/Thinkstock, B: Photodisc/Thinkstock, C: Photodisc/Thinkstock, D: Photodisc/Thinkstock
- Which two pyramids have people arranged by row in a way that can be described by an arithmetic sequence?
- How many people would it take to create a 100-level pyramid?
Share 1
With a classmate or group, tackle these tasks.
- Share and compare the different strategies used to find the number of people in a 100-level pyramid. What are the benefits and drawbacks of each strategy?
- Develop a method to determine the number of people it would take to build an n-level pyramid, where n is the number of levels in the pyramid.
![]() Save the strategy your group develops in your course folder. You will use your notes later in the lesson.
Save the strategy your group develops in your course folder. You will use your notes later in the lesson.
1.5. Explore
Module 1: Sequences and Series
Explore

AbleStock/Thinkstock
Germany’s Carl Friedrich Gauss was known as the prince of mathematicians. Gauss contributed much to the development of mathematics. Gauss was a child prodigy who had a gift for rapidly calculating complex sums in his head.
Gauss’ mathematical genius did not keep him from misbehaving at school. It is said that one of his teachers disciplined Gauss by assigning him what was thought to be a difficult task—calculating the sum of the first 100 natural numbers; in other words 1 + 2 + 3 + … + 100. Much to the surprise of his teachers and his classmates, Gauss calculated the sum in a matter of seconds! How did he do it?
As impressive as Gauss’ feat was, you don’t have to be a child prodigy to find the answer. In fact, Gauss’ problem-solving approach is simple to understand. Gauss looked at the problem from a different perspective.
In this lesson you will learn how Gauss saw the problem his teacher had given him. You will also learn to solve other problems involving the sum of the terms of arithmetic sequences.
1.6. Explore 2
Module 1: Sequences and Series
Try This 2
Retrieve the strategy you developed in Share 1 to find the number of people in n levels of a pyramid. How is this question similar to the problem posed to young Gauss? In Try This 2 you will see how Gauss saw the problem and how you can develop a way to solve similar problems.
Step 1: Print a copy of Human Pyramid.
Step 2: Use scissors to cut a triangle around each pyramid. Be sure to cut as close to the figures as you can without cutting off an arm or a head!
Step 3: Arrange the two pyramids (or triangles) into the shape of a parallelogram so that all figures are visible. Not sure what a parallelogram is? Search the Internet for an image of a parallelogram.
- How many people are in each row of the parallelogram?
- How many rows are there in the parallelogram?
- Use your answers from questions 1 and 2 to determine the number of people in one pyramid.
- Use this new method to calculate the number of people required for a 100-row pyramid. Compare this answer to the one you calculated in Share 1.

1.7. Explore 3
Module 1: Sequences and Series
Self-Check 1
In Try This 2 you found the sum of all the terms in a sequence (the total number of people in each row of the pyramid). This is referred to as an arithmetic series. Use Interactive Venn Diagram to verify the similarities and differences between arithmetic sequences and arithmetic series.
Try This 3
In Try This 3 you will work towards finding a formula to evaluate arithmetic series.
Part A
Follow these steps to evaluate the series 1 + 4 + 7 + 10 + 13 + 16 + 19.
Step 1: Evaluate the series by finding the sum of the terms on your calculator.
Step 2: Copy the series 1 + 4 + 7 + 10 + 13 + 16 + 19.
Step 3: Write the same arithmetic series underneath the original series from Step 2, but with the terms in reverse order (as shown).

Step 4: Determine the sum of each column of terms. What do you notice?
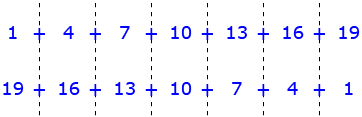
Step 5: Multiply the number of columns by the sum of each column. Compare this sum with the sum you reached in Step 1.
- What additional step should be applied to the answer in Step 5 in order to obtain the sum of the original arithmetic series?

![]() Save your responses in your course folder.
Save your responses in your course folder.
Return to Discover and try using this new method to solve the problem in Try This 1. This will make a great record of your learning for this lesson.
Part B
You will use the method you used in Part A to derive a formula to find the sum of any arithmetic series.
Recall that the general term of an arithmetic sequence is tn = a + (n − 1)d.
- For the arithmetic series 1 + 4 + 7 + 10 + 13 + 16 + 19, identify the parameters a and d.
- When working with a series, think of n as the number of terms in the series. What is the value of n for this series?
- Based on your answer from question 3, what would be the value of tn? What does tn represent in any series?

- In the last steps of Part A, you applied the following operation to find the sum of the arithmetic series:
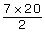
Substitute the parameters and variables you identified in Part B questions 1 to 3 for the numbers in the above expression.
1.8. Explore 4
Module 1: Sequences and Series
Turn to page 24 of the textbook to see another way the formula for determining the sum of an arithmetic series can be obtained. Note that there are two versions. Which version matches the formula you derived in Try This 3? Pay attention to how one version can be obtained from the other version.
In Try This 3 question 5 you derived a formula to find the sum of the first n terms of an arithmetic series. This formula may have looked similar to this one:
sum of the first n terms = ![]()
This formula can be rearranged to look like this:
![]()
As you read in the textbook, you will discover that another version of this formula is this:
![]()
a = the first term
n = the number of terms in the series
d = the common difference
tn = the nth term
Sn = the sum of the first n series
1.9. Explore 5
Module 1: Sequences and Series
Share 2
With a classmate, compare the general term to the series formula. So,
tn = a + (n − 1)d compared to ![]()
Then discuss the following question:
- What does each formula represent? What patterns or connections can you see between the formulas?
![]() Save notes from your discussion in your course folder.
Save notes from your discussion in your course folder.
Another way to express ![]() is
is ![]() .
.
Turn to “Example 1” on page 25 of the textbook to see how you can use either of the following formulas to solve a problem:
![]() or
or ![]()
Note that the textbook uses t1 instead of a in the general term. They are equivalent. Focus on the solution to part b. Try to answer these questions as you read:
- How do you know which formula will work best in a given situation?
- What mathematical errors can be made with each formula if you are not careful?
Add the two Sn formulas to your copy of Formula Sheet. Resave Formula Sheet in your course folder.
Self-Check 2
Complete Understanding Arithmetic Series. Have some scrap paper handy to do rough work. You may wish to save your rough work in your course folder for future reference. If you make a mistake, don’t worry! You can reset the question and then try again!
1.10. Explore 6
Module 1: Sequences and Series
Using the Sn Formulas to Evaluate Other Properties of Arithmetic Series
Besides using the two series formulas to evaluate the sum of arithmetic series, you can also use the formulas to evaluate other properties of arithmetic series. Just as you were able to use the general term tn = a + (n − 1)d to evaluate tn, a, n, and d, you can also determine all of these properties using the series formulas.
Example
Use Building an Obstacle Course to solve a problem that uses the series formulas. Pay attention to how the information provided is used to determine which formula to use.
Try This 4
You have seen an example of how you can use the Sn formulas to determine the properties of an arithmetic series. Apply what you have learned to the next problem, which is based on the same context as the example.

Goodshoot/Thinkstock
Problem
An obstacle course uses 10 log stumps. All of the logs are cut from a single log that measures 7.7 m. The difference in height between consecutive log stumps is 0.1 m. Determine the height of the shortest stump. Show your work and record each step of your solution.
![]() Save your work in your course folder.
Save your work in your course folder.
Share 3
-
Compare your answers with those of a classmate. There are different ways of solving this problem. Keep the following points in mind as you discuss your solutions:
- Do your solutions match? If not, work together to identify the error(s).
- How are your approaches different? If they are different, what are the pros and cons of each method?
- Do your solutions match? If not, work together to identify the error(s).
- Work with your classmate to find the height of the tallest stump. Try to find at least two approaches to solving this problem.
![]() Save your answers in your course folder.
Save your answers in your course folder.
Your teacher may want to look at your work to see how your collaboration with your classmate(s) has affected your learning.
1.11. Explore 7
Module 1: Sequences and Series
Turn to “Example 2” on page 26 of the textbook to see how you can use the clues to a problem and the series formula to set up a system of equations. You may recognize the system of equations from Are You Ready?
You can always use math skills you learned previously to solve problems. In this case, solving a system of equations is a skill you will use later in this course.
Self-Check 3
Complete questions 4.b., 5.a., 6.d., and 17 on pages 27 and 29 of the textbook. Show complete solutions. You may want to review relevant parts of Lesson 3 as you work through the problems. Answer
1.12. Connect
Module 1: Sequences and Series
Open your copy of the Lesson 3 Assignment, which you saved in your course folder at the start of this lesson. Complete the assignment.
Project Connection

lifeguard: Brand X/Thinkstock, Grocier: Comstock/Thinkstock, mechanic: iStockphoto/Thinkstock, yard work: Comstock/Thinkstock, fast food: Comstock/Thinkstock, waitress: Photos.com/Thinkstock,
What better way to save money than by earning it! You are now ready to tackle the next step in your project. You will be going on a job hunt to find out which jobs will be able to support your financial goals. Go to Module 1 Project: Financing your Dreams. Complete Project Connection 3: Earning Income.
Going Beyond

Comstock/Thinkstock
Have you ever helped organize a tournament? There is a lot to consider when hosting a tournament. You need to book spaces, hire referees, and provide food, not to mention working out the details of the tournament structure.
A popular tournament format is a round robin. Each team plays every other team in the tournament once. After all of the games are played, the winning team is the one that has won the most games or accumulated the most points. This is only one way of using the round-robin format.
Other tournaments use a round-robin structure for the preliminary round of play only. The highest-ranked teams after this round advance to a playoff round. In cases where it is not practical for teams to play every other team due to the large number of competitors, teams can be grouped into smaller divisions. The round-robin format is then used in each division.
Part A
You are the organizer for a sports tournament.
- How many games would you need for a round-robin tournament with the following number of teams?
- 4 teams
- 5 teams
- 4 teams
- Describe how the concepts you learned in this lesson can be applied to this problem.
- Develop a formula that can be used to determine the total number of round-robin games for n teams. Be sure to define your variables.
- Compare the formula in question 3 to the formulas you worked with throughout this lesson.
Part B
-
Imagine you are charged with creating a tournament structure for a 10-team tournament. Research the possible ways you could schedule the games. Consider these questions:
- What format will you choose? A round robin or another format?
- Will there be a playoff round after preliminary play?
- How do you seed, or rank, teams? What if there are teams that are tied?
- How many games will need to be played?
- How much space will you need to have?
- What format will you choose? A round robin or another format?
- Based on your answers in question 5, draft a mock tournament schedule that shows the following:
- all matchups in the preliminary round with start times and locations of games
- the playoff structure
- all matchups in the preliminary round with start times and locations of games
1.13. Lesson 3 Summary
Module 1: Sequences and Series
Lesson 3 Summary
© NLshop/27604676/Fotolia.com
In this lesson you investigated the following questions:
- How are arithmetic sequences and arithmetic series similar and different?
- How can you visualize the sum of an arithmetic series?
You extended your understanding of arithmetic sequences to arithmetic series. An arithmetic series is the sum of the terms of an arithmetic sequence. Both arithmetic sequences and arithmetic series have the property that consecutive terms are related by a common difference.
In general, the general term tn = a + (n − 1)d is used to determine properties of an arithmetic sequence. The formulas ![]() and
and ![]() are used to determine the properties of an arithmetic series. In the case of the general term, the parameter n refers to the position of the term; in the series formulas, n refers to the number of terms that will be added together.
are used to determine the properties of an arithmetic series. In the case of the general term, the parameter n refers to the position of the term; in the series formulas, n refers to the number of terms that will be added together.
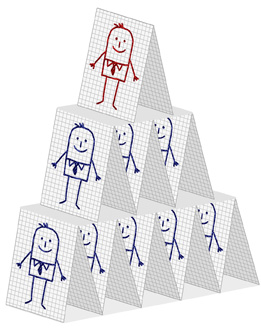
In this lesson you learned about Gauss’ method for evaluating an arithmetic series. You visualized Gauss’ method by placing two images of pyramids together. Later in the lesson you were able to build on that initial discovery to derive formulas that could be used to determine the sum of an arithmetic series.
You used the formulas to solve context-based problems. You practised using the formulas with and without rearranging. You learned to match given information within a problem with the variables of each problem. You discovered that there is more than one correct way to arrive at a solution.
You have now completed half of Module 1. In the second half of Module 1 you will explore a different kind of sequence—geometric. Geometric sequences and series can be used to describe a variety of different phenomenon, including population growth and radioactive decay. You will learn that these sequences have many applications in finance.