Lesson 4
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-1 SS |
| Book: | Lesson 4 |
| Printed by: | Guest user |
| Date: | Thursday, 4 December 2025, 2:15 AM |
Description
Created by IMSreader
1. Lesson 4
Module 1: Sequences and Series
Lesson 4: Geometric Sequences
Focus

© brankatekic/21709824/Fotolia
Do you have your driver’s license? For many people, passing their road test is a huge milestone and another step towards freedom and independence. For many parents, another driver in the family means they can share the responsibility of driving with their children. A new car, however, isn’t cheap. On top of that, there are insurance, fuel, and maintenance costs to owning a vehicle. Nevertheless, buying a car can be a thrilling experience, especially when it’s your first car!
Many people borrow money to buy a vehicle. This is called financing the vehicle. The benefit of financing is that you get to use the vehicle right away. The drawback is that you have to pay the interest on the outstanding balance after each month.
To keep things predictable for the borrower, lenders use the mathematics of sequences to determine monthly payments.
In this lesson you will investigate geometric sequences. Just as you did with arithmetic sequences, you will use discovered patterns to derive rules for determining the general term of a geometric sequence. You will also explore problems, such as those involving compound interest, that can be modelled by geometric sequences.
Outcomes
At the end of this lesson you will be able to
- identify assumptions made when identifying a geometric sequence
- provide and justify an example of a geometric sequence
- derive a rule for determining the general term of a geometric sequence
- solve a problem that involves a geometric sequence
Lesson Questions
You will investigate the following questions:
- How are arithmetic sequences and geometric sequences similar and different?
- How is compound interest an application of geometric sequences?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 4 Assignment (Download the Lesson 4 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Module 1 Glossary Terms and Formula Sheet
- work under Project Connection
Materials and Equipment
You will need a sheet of paper.
1.1. Launch
Module 1: Sequences and Series
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? Launch will help you find out.
1.2. Are You Ready?
Module 1: Sequences and Series
Are You Ready?
Complete these questions. If you experience difficulty and need help, visit Refresher or contact your teacher.
- What is a sequence? Answer
- For each arithmetic sequence, determine the general term and the value of t11.
- What is the order of operations? Answer
- Evaluate each of the following expressions.
How did the questions go? Depending on your answer, skip forward to Discover or work through Refresher.
1.3. Refresher
Module 1: Sequences and Series
Refresher
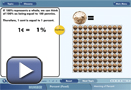
Use Math Continuum: Percent (Food) to review concepts relating to percentage. In the first topic you will review the definition of percent. In the second topic you will practise determining equivalent percents, fractions, and decimals. In the final topic, you will play a game that tests your knowledge of percents and your reflexes!
To get started, select “Percent (Food)” under the “Number” column. Then start with the first topic.
Next, look at the definition in Sequence. You may want to retrieve your copy of Module 1 Glossary Terms to update your definition of sequence.
Review the basic properties of arithmetic sequences by revisiting Direct and Partial Variation: Arithmetic Sequences. This applet also reviews the relationship between arithmetic sequences and linear functions. Work through slides 1 to 11. Remember that any linear function with a y-intercept of zero exhibits direct variation, and any linear function with a non-zero y-intercept represents partial variation.
Use Order of Operations to remind yourself how to evaluate expressions that involve multiple mathematical operations. The applet includes three examples of varying difficulty.
Go back to the Are You Ready? questions and try them again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 1: Sequences and Series
Discover
How many times can you fold a piece of paper in half? You will answer that question in this Math Lab. You will also learn something about another type of sequence.
Problem
Given a sheet of paper, how do the number of half-folds affect the number of layers?
Materials
You will need a sheet of paper.
Procedure
| Step 1: Construct a table similar to the table shown. |
|
|||||||||||||||
| Step 2: Measure the dimensions of the sheet of paper, and calculate the area. Record your answer in the third column of the table. |  |
|||||||||||||||
| Step 3: Fold the paper in half. In your table, record the area of the new rectangle formed and the number of layers of paper. |  |
|||||||||||||||
| Step 4: Repeat Step 3 as many times as possible. You will need to add several rows to your table. |
Analysis
- Identify, compare, and describe all the patterns you observe in the table.
- Develop a method to find the following values:
- the number of layers after the 16th fold
- the area of the rectangle after the 16th fold
- the number of folds required to have 16 384 layers
- the number of layers after the 16th fold
![]() Save your work in your course folder. You will use your notes later in the lesson.
Save your work in your course folder. You will use your notes later in the lesson.
Did You Know?
In 2002, high school student Britney Gallivan (of Pomona, California) folded a very long sheet of toilet paper in half 12 times. Prior to that, it was popularly held that no sheet of paper could be folded more than 7 times. The toilet paper measured approximately 1200 m in length! Britney also derived a formula that related the properties of a piece of paper to the maximum number of times the paper could be folded in half. Ms. Gallivan’s mathematical feat has been featured in television documentaries and even on an episode of the television show Numb3rs.
1.5. Explore
Module 1: Sequences and Series
Explore

A pyramid scheme is a fraudulent money-making scam. These schemes are illegal because they deceive people by promising huge sums of money. The idea of a pyramid scheme is based on a person or group of people recruiting other people. Those who have been recruited pay a fee to the recruiter.
The recruited individuals, in turn, recruit more people who also pay a fee. The fees are distributed to those who are higher up in the pyramid. To make money in this scheme, you must have many levels of recruited individuals beneath you.
The illustration shows an example of how a pyramid scheme works. In this example each recruited person recruits six other people. Do you think this practice can continue on forever?
The number of people recruited at each level forms a sequence. In this lesson you will investigate sequences of this kind. You will discover whether a pyramid scheme is sustainable. You will determine the general term for these sequences, and you will use the general term to solve problems related to finance and other applications.
You already saved Module 1 Glossary Terms in your course folder. In this lesson, you will define the following terms, and maybe others, in your copy of Module 1 Glossary Terms:
- geometric sequence
- common ratio
- compound interest
Geometric Sequence and Common Ratio
As you folded paper in Math Lab, you might have noticed the pattern, or sequence, related to the number of layers after each fold: 1, 2, 4, 8, ….
Can you see a common difference between each term in the sequence? You have already studied arithmetic sequences in which terms always increase or decrease by the same value. In this example, the difference between each term changes; therefore, there is no common difference and the sequence is not arithmetic.
In this sequence, you multiply each value by 2 to obtain the value of the next term. This is an example of a geometric sequence. In this case, the constant, 2, is known as the common ratio.
![]()
1.6. Explore 2
Module 1: Sequences and Series
Try This 1
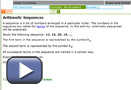
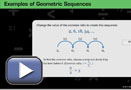
- Work through Examples of Geometric Sequences. Find the common ratio, and then use the common ratio to extend each sequence.
-
Consider the following sequences.
A 3, 15, 75, 375, 1875, … B 8, 12, 18, 27, … C −5, −10, 20, 40, −80, −160, … D 1215, 405, 135, 45, …, 
E 2, 4, 8, 16, 32, 64, 128, 254, 508
-
How are the first three sequences different?
- Which of the sequences are geometric? How do you know?
-
How are the first three sequences different?
Challenging Assumptions
Not all sequences that appear to be geometric are, in fact, geometric. This lesson has assumed that if the first few terms of an infinite sequence show a geometric pattern, the rest of the sequence is also geometric.
Generally, the more terms a sequence shows, the safer it is to assume the sequence has a particular pattern. On the other hand, if only a few terms are shown, there may be other possible patterns governing the progression.
How many terms must be revealed in a sequence before you can confidently identify the sequence as geometric? Think about this as you complete Try This 2.
Try This 2
- Consider the sequence 1, 2, …. What are some possible values for the next term in the sequence? State two possibilities and describe the reasons behind your choices.
- Consider the sequence 1, 2, 4, …. Are there enough terms shown that you can be certain this is a geometric sequence? Can you find any other pattern in these three terms that would not result in 8 as the 4th term?
![]() Save your answers in your course folder.
Save your answers in your course folder.
You will explore this concept further if you choose to complete Going Beyond later in this lesson.
Self-Check 1
Check your understanding by completing the following interactive activities:
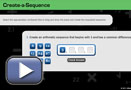
- Create-a-Sequence
- Combining Sequences
- Identifying the Common Ratio
1.7. Explore 3
Module 1: Sequences and Series
Try This 3

© Vasiliy Koval/259778/Fotolia
Retrieve your work from the Math Lab. You may have found that you can only fold a sheet of paper fewer than 10 times. Assume that you can fold a piece of paper indefinitely. You could then use the pattern to determine a formula for the general term of a geometric sequence.
- Copy the information from the “Layers” column of your table into the second column of the following table. The first three rows have been done as an example. Complete all rows in your table.
Term Position Term Value Expression t1 1 1 t2 2 1 × 2 t3 4 1 × 2 × 2
- Now you can repeat the same exercise in the general case. Create and complete a second table, such as the one shown here. Assume that the first term is a, and the common ratio is r. Rewrite the expressions from the table in question 1 using a and r. The first three rows have been completed for you.
Term Position Expression t1 a t2 a × r = ar t3 a × r × r = ar2
-
Compare the term position in the sequence and the expression. What pattern do you see?

-
Use the pattern you identified to determine an expression for the general term tn.
Share 1
Work with a classmate or in a group.
- Compare your expression for the general term tn from Try This 3. If the expressions vary, discuss reasons for the differences and try to agree on the correct expression. You may want to search the textbook or the Internet for a formula for the general term of a geometric sequence.
- Use your expression to build the general term that could be used to describe the geometric sequence representing the number of people in each level of the pyramid scheme introduced at the beginning of Explore.

- Consider the sequence 24, 36, 54, 81, ….
- How do you know this is a geometric sequence? What assumption are you making?
- What is the common ratio?
- What is the general term that describes the sequence?
- How do you know this is a geometric sequence? What assumption are you making?
![]() Save your work in your course folder. Ask your teacher if you should submit your work for feedback.
Save your work in your course folder. Ask your teacher if you should submit your work for feedback.
1.8. Explore 4
Module 1: Sequences and Series
The General Term of a Geometric Sequence
Recall that the general term is the formula that describes the terms of a sequence. In Try This 3, you may have discovered that the general term of a geometric sequence is as follows:
tn = arn−1 ![]()
As a rule, you can use the general term to solve problems related to specific terms of a geometric sequence.
tn = the value of the nth term
a = the first term of the sequence
r = the common ratio
n = the position of the term
Turn to page 35 of the textbook. Read “Example 2” and study the solution. Pay careful attention to the following:
- how the general term is established
- the order in which the number operations are performed
Remember that the general term in the textbook uses t1 in place of a.
Self-Check 2
Complete Geometric Sequence Self-Check.
1.9. Explore 5
Module 1: Sequences and Series
Try This 4

iStockphoto/Thinkstock
The world’s largest free-standing totem pole is located in Beacon Hill Park in Victoria, British Columbia. The pole is approximately 128 ft tall.
Imagine that an eagle with a golf ball clasped in its talons is perched at the top of the totem pole. As it flies away, the eagle drops the ball. The ball bounces to 65% of its previous height.
Figure 1
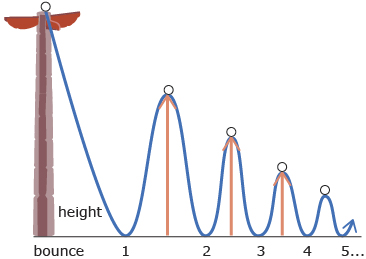
Assume that the ball continues to bounce to 65% of its previous height.
- Calculate and label the first four bounce heights shown in Figure 1.

- The bounce heights in this problem form a sequence. Write the general term for the sequence.

- Use the general term to find the height the ball reaches after the 9th bounce.

![]() Save your work in your course folder.
Save your work in your course folder.
1.10. Explore 6
Module 1: Sequences and Series
Compound Interest
Recall that a pyramid scheme is a fraudulent money-making scam that cheats many people out of their money. Despite the existence of pyramid schemes and other scams, there are a large number of legitimate ways to invest your money. For example, you may invest your money in a savings account, Guaranteed Investment Certificate (GIC), or Canada Savings Bond to name a few. These investments pay compound interest.
In Try This 3 and Share 1 you derived the general term of a geometric sequence. Now you can derive the formula for evaluating compound interest. As you watch Deriving a Formula for Compound Interest, think about how you would answer the following questions:
- How is compound interest an example of a geometric sequence? What is the first term? What is the common ratio?
- How was the process of deriving the formula for compound interest similar to the process for deriving the general term of a geometric sequence?
- How would you use the formula to determine the following?
- P
- i
- P
- How is the formula A = 800(1.1)n different from the general term tn = 800(1.1)n−1?
Share 2
With a classmate, answer the four questions you thought about as you watched Deriving a Formula for Compound Interest. Record your solutions and show support for your reasoning.
![]() Save your work in your course folder.
Save your work in your course folder.
Your teacher may look at your work to gauge your progress and provide feedback.
1.11. Explore 7
Module 1: Sequences and Series
Try This 5

Go to your course folder and retrieve your work from Lesson 2 Try This 1. In that exercise you investigated the investment of $1000 in a savings bond that pays 4% simple interest at the end of every year. The investment earned $40/yr. The value of the investment at the end of each year formed an arithmetic sequence.
In the video Deriving a Formula for Compound Interest, you solved a problem involving the investment of $1000 in a savings bond that pays 4%/yr compounded annually. The value of the investment at the end of each year formed a geometric sequence.
- In what ways are these problems similar? In what ways are they different?
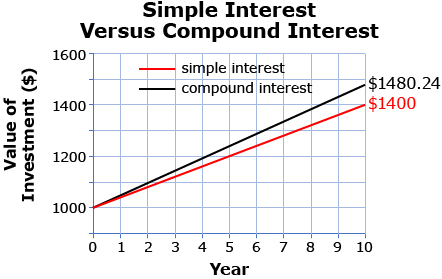
- In Lesson 2 Try This 2, you created a graph relating the value of the investment over the first 10 yr. Create a new graph relating the value of the compound-interest investment over the first 10 yr.
- What conclusions can you draw about compound interest as compared to simple interest?
- Which investment, the investment with simple interest or the investment with compound interest, is worth more at the end of 10 yr? By approximately how much?

1.12. Explore 8
Module 1: Sequences and Series
Go to the textbook to see how you can use either logical reasoning or the general term to solve a problem related to geometric sequences. On pages 36 to 37, work through “Example 3.” This problem is different from what you have already encountered because you are given neither the first term nor the common ratio. Instead, these are the very values that you are required to find! Which method do you like better? What other variations are there for solving the problem?
Try This 6
You have derived and applied the general term tn = arn−1 to solve problems involving geometric sequences. What is the key characteristic of geometric sequences? Try This 6 challenges your understanding of geometric sequences.
Your task is to solve the problem. Think about the problem, and then try one or more ways of solving the problem. If you get stuck, ask for a hint.
Three terms of a geometric sequence are x + 4, x, x − 3. Determine the value of each term.
![]()
![]()
![]()
![]()
![]()
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 3
With a partner, compare and discuss your solutions. Use the following questions as a guide for your discussion.
- What is the key understanding that is required to solve this type of problem?
- Is the common ratio greater than 1 or less than 1? How could you have determined the answer to this question without solving for r?
- Compare your method with your partner’s method. In what ways are your methods similar? In what ways are your methods different? Are the methods based on the same key principles?
- In what ways can you verify that you have the correct solution?
![]() Save your responses in your course folder.
Save your responses in your course folder.
Self-Check 3
Complete questions 9, 14, 23, and 25 on pages 40 to 44 of the textbook. Remember to show your work and review parts of this lesson if you need to. Answers
1.13. Connect
Module 1: Sequences and Series
Open the Lesson 4 Assignment you saved in your course folder at the start of this lesson. Complete the assignment.
Project Connection
In this lesson you investigated the formula for compound interest. In your Module 1 Project you will research different investment vehicles, or ways to invest. You will create an investment plan to help finance your goals. Go to Module 1 Project: Financing Your Dreams. Complete Project Connection 4: Investing.
Going Beyond
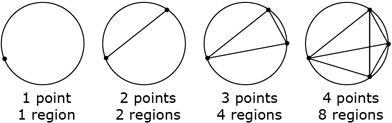
Some patterns that appear to be geometric may not be! Study the illustration, and then complete the following tasks.
- Construct a 5th circle that passes through 5 points. Draw line segments joining each pair of points, making sure that no three line segments ever intersect at a common point within the circle. Count the number of regions in this circle. Does this satisfy the geometric pattern?
- Predict how many regions you would expect to find on a circle with 6 points.
- Repeat the steps in question 1 for a circle with 6 points. Compare your result with your prediction from question 2.
- Continue to investigate the number of regions when there are 7 and 8 points on the circle. Research to find out if you can determine a formula for the pattern.
![]() Save your results in your course folder.
Save your results in your course folder.
1.14. Lesson 4 Summary
Module 1: Sequences and Series
Lesson 4 Summary
In this lesson you investigated the following questions:
- How are arithmetic sequences and geometric sequences similar and different?
- How is compound interest an application of geometric sequences?
You studied geometric sequences. The following table summarizes the similarities and differences between arithmetic and geometric sequences.
| Arithmetic Sequence | Geometric Sequence | ||
An arithmetic sequence is a sequence in which the next term equals the preceding term plus or minus a common difference (d).
Recall the general term formula is
where a is the first term, n is the position of the term, and d is the common difference. Common difference: d = t2 − t1 (or any term minus the previous term) |
A geometric sequence is a sequence in which the next term is equal to the preceding term multiplied or divided by a constant ratio (r).
Recall the general term formula is
where a is the first term, n is the position of the term, and r is the common ratio. |
Geometric sequences can be applied in many situations. One such situation is compound interest. You compared the formula for compound interest, A = P(1 + i)n, to the general term. In the case of compound interest, the first term is the principal and the common ratio is 1 + i.
You also compared simple-interest growth to compound-interest growth. Over time, an investment earning compound interest increases in value more rapidly than the same investment earning simple interest.
In the next lesson you will extend your study of geometric sequences to geometric series.