Lesson 5
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-1 SS |
| Book: | Lesson 5 |
| Printed by: | Guest user |
| Date: | Thursday, 4 December 2025, 2:08 AM |
Description
Created by IMSreader
1. Lesson 5
Module 1: Sequences and Series
Lesson 5: Geometric Series
Focus

Stockbyte/Thinkstock
In an earlier lesson you started to think about your financial goals. These may include major purchases, such as a house or a car. You may have also considered putting money away for college or university, or for an overseas trip.
While each of these goals is worthwhile in its own right, the goals are not equal from an investment perspective. The value of the car depreciates over time—in other words, the car’s value goes down as the car ages. A backpacking trip to Europe may provide a lifetime of memories and character-building experiences; however, there is no monetary return on the investment—you cannot make any money from the trip.
There are also examples of financial goals that appreciate, or increase, in value over time. One example of this is your post-secondary education. In fact, generally speaking, the more education you have, the higher your earning power after graduating. Another example of an appreciating asset is a house. Homes these days are expensive, but past experience shows that houses increase in value over the long run.
This lesson is about geometric series. A geometric series can be used to determine the value of an investment when monthly contributions are made. You will derive and use formulas relating to geometric series. You will study the contexts in which those formulas can be applied, and you will gain an understanding of how geometric series relate to finance.
Outcomes
At the end of this lesson you will be able to
- derive a rule for determining the sum of n terms of a geometric series
- determine t1, r, n, or Sn in a problem that involves a geometric series
- solve a problem that involves a geometric series
Lesson Questions
You will investigate the following questions:
- In what ways can mathematical formulas be derived?
- How are geometric series used in finance?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 5 Assignment (Download the Lesson 5 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Module 1 Glossary Terms and Formula Sheet
- work under Project Connection
1.1. Launch
Module 1: Sequences and Series
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? Launch will help you find out.
1.2. Are You Ready?
Module 1: Sequences and Series
Are You Ready?
Before beginning this lesson you should be able to
- solve problems involving geometric sequences
- apply the product law of exponents
Complete these questions. If you experience difficulty and need help, visit Refresher or contact your teacher.
- Consider this geometric sequence:
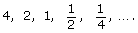
- What is the difference between a sequence and a series? Give an example of each. Answer
- Use the product law of exponents to simplify the following expressions:
How did the questions go? Depending on your answer, skip forward to Discover or work through Refresher.
1.3. Refresher
Module 1: Sequences and Series
Refresher
Work through Geometric Sequences and Exponential Functions to review geometric sequences and the variables and parameters associated with them.
To review problem solving using geometric sequences, read the example questions on pages 34 and 35 of the textbook.
To review arithmetic series, go to page 24 of the textbook and look at the two blue boxes containing formulas that can be used to evaluate the sum of an arithmetic series. See how these formulas are applied in “Example 1” and “Example 2” on pages 25 and 26.
Use Exploring Laws of Exponents to review the product law of exponents. Select the first box, which represents the product law. You may also want to explore some of the other laws.
Go back to the Are You Ready? section and try the questions again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 1: Sequences and Series
Discover

© Gyuzel/12025674/Fotolia
Try This 1
Legend has it that the game of chess was invented for a Persian king by one of his servants. The king asked the servant how he would like to be paid for the game. The servant stated that he would like one grain of rice to be placed on the first square of the chessboard, two grains of rice to be placed on the second square, four grains of rice on the third square, eight grains of rice on the fourth square, and so on. Each subsequent square was to have twice as many grains of rice than the previous square.
- Complete the chart.
Square
1 2 3 4 5 6 7 8 9 10 Number of Grains of Rice in the Square
1 2 4
- Write an expression that represents the numbers of grains of rice, R, on the nth square of the chessboard.
- Determine the total number of grains of rice in the first
- 5 squares
- 9 squares
- 5 squares
- Analyze your answers to question 3. Describe a strategy that could be used to determine the total number of grains of rice in the first n squares.
![]() Save your results in your course folder.
Save your results in your course folder.
Share 1
- Share your strategies with a partner. Find out the total number of grains of rice up to and including 15 squares or more. Compare your strategies with your partner's strategies to see if both strategies yield identical results.
- Describe how the strategy could be adapted to solve the following similar problem:
A second servant solved another problem for the king. Granted the same wish as his companion, the second servant asked for 2 grains of rice on the 1st black square, 8 grains of rice on the 2nd black square, 32 grains on the 3rd black square, and so on. Each subsequent black square was to have four times as many grains of rice than the previous black square.
![]() Save your results in your course folder. You will use these results later in the lesson.
Save your results in your course folder. You will use these results later in the lesson.
1.5. Explore
Module 1: Sequences and Series
Explore
How would you like to put your money to work for you? Compound interest has the power to make you rich! In the last lesson you compared graphs of simple-interest growth to graphs of compound-interest growth. You saw that, as time passes on, the value of a compound-interest investment grows at a much faster rate than that of a simple-interest investment.

© DIDEM HIZAR/13714776/Fotolia.com
In fact, a 15-year-old who invests $200/mo for 10 yr will have earned more money by the time she is 65 years old than a 25-year-old who invests $200/mo for 40 yr! It really pays to start investing early!
In this lesson you will study geometric series. You will derive formulas for evaluating any given geometric series, and you will apply those formulas to relevant contexts. You will also see that, if you make monthly contributions to your investment plan, the power of compound interest can make your money work for you.
You already saved Module 1 Glossary Terms in your course folder. In this lesson, you will define the following term, and maybe others, in your copy of Module 1 Glossary Terms:
- geometric series
Recall that an arithmetic series is the sum of the terms of an arithmetic sequence. Does this help you define a geometric series? Remember to check your definition against information you find on the Internet, in the textbook, or elsewhere.
1.6. Explore 2
Module 1: Sequences and Series
Determining the Sum of a Geometric Series
In Lesson 3 you derived the formulas for evaluating an arithmetic series by applying Gauss’ method. The method was first applied to a specific series, and then the method was applied to the general case.
Watch Sum of a Series Pop! to see one strategy for determining the sum of a geometric series. As you watch, pay attention to the pop-up bubbles that appear. You may want to pause the video at these points in order to think about the questions in the pop-ups.
You have now been exposed to two possible ways to find the sum of a series:
- the way used in the chessboard activity from Try This 1
- the way used in Sum of a Series Pop!
Try This 2
In Try This 2 you will construct a formula to describe the sum of any geometric series. You will use the method from Sum of a Series Pop! However, instead of beginning with a specific geometric series, you will begin with a general geometric series made up of variables.
Begin with a general geometric series written in full:
Sn = a + ar + ar2 + ar3 + ![]() + arn−1
+ arn−1
Use this general series and Geometric Series Proof Sorter to construct a formula to describe the sum of any geometric series.
1.7. Explore 3
Module 1: Sequences and Series
Formula for a Geometric Series
You should have discovered that the formula for the sum of a geometric series can be expressed as
![]()
This is a good time to add the formula for the sum of a geometric series to your copy of Formula Sheet.
Note that one part of this formula is rn − 1. Do not mistake this for rn−1, which is an expression that you would find in the general term tn = arn−1. You should make a note of this in your copy of Formula Sheet.
Examine the variables in the formula for finding the sum of a geometric series.
![]()
![]()
Why is there a restriction on this formula that r ≠ 1? What happens if r = 1? Find out by replacing r with 1.
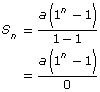
You can see that when r = 1, the denominator of the fraction becomes 0. This is undefined and is not possible. That is why r ≠ 1.
Can you create a geometric sequence where r = 1? What would the series look like? ![]()
Try This 3
Retrieve your work from Try This 1. In question 3.b. you had to determine the total sum of the grains of rice on 9 squares of a chessboard. Use the geometric series formula to confirm your answer from Try This 1.
You will need to identify the values for t1, r, and n. Substitute the appropriate values into the series formula, and then evaluate. Need a hint?
What is t1? ![]()
What is r? ![]()
What is n? ![]()
How do I substitute values? ![]()
How many grains of rice are there in total? ![]()
Mistakes can easily be made when working with negative numbers. Watch Evaluating a Power with a Negative Base to see a common error that arises when using the series formula to evaluate a power with a negative base, such as −23.
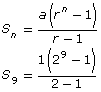
Sn = the sum of the first n terms of the geometric series
a = the first term of the geometric series
r = the common ratio
n = the number of terms in the geometric series
1.8. Explore 4
Module 1: Sequences and Series
Self-Check 1
Complete Geometric Series Formula Self-Check. Have some scrap paper handy to do rough work. You may wish to save your rough work in your course folder for future reference. If you make a mistake, don’t worry! You can reset each question, and then try again!
Try This 4
You have derived a formula that can be used to evaluate the sum of a geometric series when given the first term (a), the common ratio (r), and the number of terms (n) in the series. Is it possible to determine the sum of a geometric series if you are not given all of these values?
Use Find the Parameter Values to explore this problem.
1.9. Explore 5
Module 1: Sequences and Series
Try This 5
In Try This 4 you most likely had to determine the number of terms in the series before using the geometric series formula you derived earlier in the lesson. Instead, you could have solved the problem by using a formula that doesn’t contain the variable n but will still find the sum of the series. You will create a formulato do this by combining two formulas in this Try This activity.
Using the formulas ![]() and tn = arn−1, try to construct a new formula that does not include the variable n. Need help? Take a hint.
and tn = arn−1, try to construct a new formula that does not include the variable n. Need help? Take a hint.
![]()
![]()
![]()
Turn to pages 50 and 51 in the textbook to review an example of how the sum of a geometric series can be evaluated when you do not know how many terms are in the series. Two methods are presented. Which method do you prefer?
As you read, try to duplicate the results with your calculator. This will ensure you are entering the information into your calculator the right way.
Take a moment to add the alternate geometric series formula to your copy of Formula Sheet.
Self-Check 2
Complete Geometric Sum Formula Self-Check. Have some scrap paper handy to do rough work. You may wish to save your rough work in your course folder for future reference. If you make a mistake, don’t worry! You can reset each question, and then try again!
1.10. Explore 6
Module 1: Sequences and Series
Geometric Series and Investing
In the introduction to Explore you read that a 15-year-old who invests $200/mo for 10 yr will have earned more money by the time she is 65 years old than a 25-year old who invests $200/mo for 40 yr. You now have the mathematical know-how to be able to prove this statement.
The following example will show you the total value of the 15-year-old’s investment. Work through the example to see how the concepts of geometric series are used to determine the answer. Then use the same principles to determine the value of the 25-year-old’s investment.
Example
Ming, a 15-year-old, contributes $200/mo towards an investment that pays 9%/yr compounded monthly. She pays $200 at the beginning of every month for 10 yrs. She then stops contributing to the investment, allowing the investment to continue accumulating interest. Determine the total value of the investment when Ming is 65 years old.
Solution
| Value to be Determined | Calculation | Reasoning |
| number of months in 10 yr | 10 yr × 12 mo/yr = 120 mo | There are 120 mo in 10 yr. |
| interest rate per month | 9% ÷ 12 = 0.75% | The monthly interest is 0.75%. For the purposes of calculations using the compound interest formula, you will use 0.0075 to represent i. |
| value of the 1st $200 contributed | 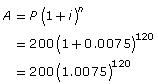 |
The first $200 will earn interest for the full 10 yr, or 120 mo. |
| value of the 2nd $200 contributed | 200(1 + 0.0075)119 = 200(1.0075)119 |
The second $200 will earn interest for the full 10 yr less 1 mo, or 119 mo altogether. |
| value of the 3rd $200 contributed | 200(1 + 0.0075)118 = 200(1.0075)118 |
The third $200 will earn interest for the full 10 yr less 2 mo, or 118 mo altogether. |
A geometric series can be formed, where the first three terms are:
200(1.0075)120 + 200(1.0075)119 + 200(1.0075)118 + ![]() + 200(1.0075)2 + 200(1.0075)1
+ 200(1.0075)2 + 200(1.0075)1
| Value to be Determined | Calculation | Reasoning |
| sum of the geometric series |  |
The total value of the investment after 10 yr is $38 993.13. |
| amount of time the investment is allowed to earn interest after the initial 10 yr of contributions | 65 − 25 = 40 yr 40 yr = 40 × 12 = 480 mo |
Ming will be 25 years old when she pays her final $200 contribution. The investment will now gain interest for 40 more years until she is 65 years old. |
| value of the investment when Ming is 65 | 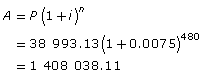 |
Ming’s investment will be worth $1 408 038.11. |
1.11. Explore 7
Module 1: Sequences and Series
Self-Check 3
To score an eagle in the game of golf means to score two under par. This means that the ball was hit into the hole using two strokes less than expected. Eagles typically occur on par-5 holes.

Hemera/Thinkstock
Mrs. Richards, Ming’s math teacher, is 25 years old. She contributes $200/mo towards a similar investment that pays 6%/yr compounded monthly. The difference is that Mrs. Richards plans to continue contributing $200/mo until she retires at 65 years of age.
- Determine the total value of the investment when Mrs. Richards is 65 years old. Answer
- Who has earned more money? By how much? Answer
- Compare the amount of money that Ming will have invested versus the amount that Mrs. Richards will have invested. Explain who will be the more successful investor. Answer
Self-Check 4
Recall the problem in Lesson 4 of the eagle dropping the golf ball from the top of a totem pole. In that lesson you considered the height of the ball after each bounce. In this Self-Check you will revisit that problem in order to determine the total vertical distance travelled by the ball after a given number of bounces.
![]() Go to your course folder. Retrieve your answers to Lesson 4 Try This 3.
Go to your course folder. Retrieve your answers to Lesson 4 Try This 3.
Work through Bouncing Ball to reacquaint yourself with the situation. At certain places in the animation, you will be asked to type in responses. Use your solutions from Lesson 4 and the knowledge you have gained in this lesson to complete the questions.
Self-Check 5
Turn to pages 54 and 56 in the textbook. Complete questions 9, 10, 11, and 15. You may want to review relevant parts of the lesson as you work through the problems. Answers
1.12. Connect
Module 1: Sequences and Series
Open the Lesson 5 Assignment you saved in your course folder at the beginning of this lesson. Complete the assignment.
Project Connection
In this lesson you investigated geometric series. In your Module 1 Project you will use geometric series to develop a monthly savings plan. Go to Module 1 Project: Financing Your Dreams, and complete Project Connection 5: Monthly Savings Plan.
Going Beyond

In Lesson 4 and Lesson 5 you considered the height of a bouncing ball. You can test the assumptions of these problems by conducting your own experiment with a bouncing ball.
One of the assumptions in these problems is that a ball will consistently bounce to a certain fraction of the previous height. Do you think this is true? Test your hypothesis on several balls with different bounce heights. You may want to try a tennis ball, a ping-pong ball, or a basketball.
Design an experiment to see how consistently a ball bounces to a percentage of the previous height. For how many bounces does this consistency last? What is the maximum number of countable bounces before the ball stays on the ground?
In the next lesson you will consider the sum of an infinite number of terms. If a ball were to bounce infinitely, what would be the total vertical distance travelled by the ball? How could you verify your prediction?
![]() Save your experimental design and your results in your course folder.
Save your experimental design and your results in your course folder.
Check with your teacher to see if your work should be submitted.
1.13. Lesson 5 Summary
Module 1: Sequences and Series
Lesson 5 Summary
In this lesson you investigated the following questions:
- In what ways can mathematical formulas be derived?
- How are geometric series used in finance?
Geometric series represent the sum of the terms of a geometric sequence. It is not always convenient to add the individual terms of a geometric series due to the large number of terms. In this lesson you derived two formulas that can be used to determine the sum of any number of terms in a geometric series.
You practised two commonly accepted approaches for formula derivation. The first approach is to start with a specific case using actual numerical values. The general case, or formula, is then deduced by substituting variables for the numerical values. This is the method you used to derive the first geometric series formula, ![]()
The second approach involves combining known formulas or relationships to create a new formula. This is the method you used to derive the second geometric series formula. For the second formula, you combined the general term of a geometric sequence with the first geometric series formula. This created ![]()
You also investigated problems that can be solved with geometric series, such as the problem of the bouncing ball and the investment questions in Project Connection.
In the final lesson of this module you will consider how you can add the terms of an infinite geometric series.