Lesson 6
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-1 SS |
| Book: | Lesson 6 |
| Printed by: | Guest user |
| Date: | Thursday, 4 December 2025, 2:15 AM |
Description
Created by IMSreader
1. Lesson 6
Module 1: Sequences and Series
Lesson 6: Infinite Geometric Series
Focus

Boat: iStockphoto/Thinkstock, Skydivers: Photodisc/Thinkstock, Family: liquidlibrary/Thinkstock
Do you have a list of goals you dream of accomplishing one day, perhaps when you retire? Some people refer to these goals as a bucket list. To others, they are just a list of goals. Either way, your dreams will need to be financed.
Visiting exotic destinations or embarking on a once-in-a-lifetime adventure costs money. Maybe your idea of a satisfying retirement is to stay close to home and indulge in a hobby or volunteer in your community. Either way, you will still need a steady income to maintain your daily expenses.
All working Canadians contribute to the Canada Pension Plan, which pays Canadians a monthly pension. Many Canadians also invest additional income in retirement savings plans. Upon retirement, Canadians draw on their pension, savings, and investments to provide a steady source of income. Ideally, this income will allow them to live comfortably and enjoy items on their bucket lists!
In this lesson you will investigate infinite geometric series. You will see that it is possible to predict the sum of an infinite number of terms. You will also learn how you can apply infinite geometric series to calculate the value of annuities paid over an indefinite period. By doing this, you can make informed decisions to secure your financial future.
Outcomes
At the end of this lesson you will be able to
- generalize, using inductive reasoning, a rule for determining the sum of an infinite geometric series
- explain why a geometric series is convergent or divergent
- solve a problem that involves an infinite geometric series
Lesson Questions
In this lesson you will investigate the following questions:
- When is it possible to add an infinite number of terms?
- How are infinite sums used in finance?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 6 Assignment (Download the Lesson 6 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Module 1 Glossary Terms and Formula Sheet
- work under Project Connection
1.1. Launch
Module 1: Sequences and Series
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? Launch will help you find out.
1.2. Are You Ready?
Module 1: Sequences and Series
Are You Ready?
Before beginning this lesson you should be able to
- convert decimals to reduced fractions
- define terms related to sequences and series
- solve problems involving geometric sequences
Complete these questions. If you experience difficulty and need help, visit Refresher or contact your teacher.
- Complete a table like this one by converting each of the following decimals into fractions in the form
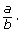 Reduce to the simplest form where possible.
Reduce to the simplest form where possible.
Decimal
Fraction
0.3
3.78
0.012
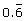
Answer
- Identify the difference between each of the following terms.
-
Consider the geometric sequence 5, 10, 20, 40, ….
- Define the word “infinite.” Give an example of something that is infinite. Answer
How did the questions go? Depending on your answer, skip forward to Discover or work through Refresher.
1.3. Refresher
Module 1: Sequences and Series
Refresher
Watch “Decimals and Fractions” to review converting decimals into reduced fractions.
Go to Sequence to review the definition of sequence and the difference between a finite sequence and an infinite sequence. You might also review your copy of Module 1 Glossary Terms to review the differences between arithmetic sequences and geometric sequences, and sequences and series.
To review how to construct and evaluate the general term of a geometric sequence, turn to “Example 2” on page 35 of the textbook. To review how to determine the sum of a geometric series, turn to “Example 1.a.” on page 49 of the textbook.
Search the Internet for a definition of infinite. You can type “define: infinite” to find definitions.
Go back to the Are You Ready section and try the questions again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 1: Sequences and Series
Discover
Try This 1
- Assume you order a small pizza for lunch. The pizza is cut into four slices. You eat one slice of pizza in the first minute. After that, you don’t feel as hungry. In the next minute, you eat only one-quarter of a slice. In the third minute, you eat one-quarter of a quarter-slice. If this pattern continues, when will you finish the pizza? Is it possible that you will not finish the pizza even if you had all the time in the world?

© Joe Gough/4922965/Fotolia
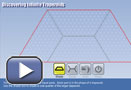
In mathematics, if you add an infinite number of terms together, will the sum always be equal to infinity? Use Discovering Infinite Trapezoids to simulate the addition of an infinite number of terms.
- If you were to continue dividing and shading the trapezoid according to the procedure in Discovering Infinite Trapezoids, what fraction of the original trapezoid will be shaded after an infinite number of steps? You may want to go back to the applet to try shading different parts of the trapezoid in order to better estimate the fraction of the original trapezoid that is shaded.
![]() Save your response in your course folder.
Save your response in your course folder.
Capture the final image of your partially shaded trapezoid and save that image in your course folder.
Not sure how to capture the image? You might use the PrtSc key on your keyboard, which is to the right of the F12 key. When the image you want to capture is on your computer monitor, press the PrtSc key. Open a blank document, such as a Word document, and paste the image into the document.
Remember to save the document containing your image. You will revisit this information later in the lesson.
1.5. Explore
Module 1: Sequences and Series
Explore

Comstock/Thinkstock
The money you save towards your retirement years is often referred to as your nest egg. The nest egg is built up during your working years. The nest egg increases in size as a result of regular contributions to your investment and interest earnings.
In retirement, you can have your nest egg paid out to you in a series of regular payments, called an annuity. Depending on the amount of money in the nest egg and the size of the annuity, you could make your retirement savings last a very long time.
An annuity that continues forever is called a perpetuity. Do you see a way you could turn your retirement savings into a perpetuity?
In this lesson you will study infinite geometric series. You will extend your knowledge of geometric series to an infinite number of terms. You will learn how to identify those infinite geometric series with sums versus those without. You will derive formulas for evaluating an infinite geometric series. You will also solve problems involving these types of series.
1.6. Explore 2
Module 1: Sequences and Series
What Is the Sum of an Infinite Number of Terms?
Think back to Lesson 5 Try This 1. In that activity you investigated a geometric pattern involving grains of rice on consecutive squares of a chessboard. You discovered that each time you advanced to the next square, the total number of grains of rice increases. Indeed, the sum of the series did not get close to any particular number—the sum only increased in size dramatically as more terms were added.
It would seem logical that as you add more terms to an existing sum, the resulting sum grows larger. As you continue to add even more terms, the result approaches infinity. Therefore, you can assume that the sum of an infinite number of terms is infinity. Despite this logic, however, Try This 1 in this lesson shows that this does not hold true in all cases.
Watch Discovering Infinite Trapezoids Video to see one way in which a student might have completed Try This 1. The video only shows the process of dividing and shading trapezoids a few times. Ask yourself what the diagram would look like if it were actually possible to shade an infinite number of trapezoids.
- How would you describe the shape of the shaded area?
- What fraction of the whole trapezoid would this shaded area represent?
You have seen in the video that the sum of an infinite number of terms can approach a finite number! It seems that as you add more area, the total area does not get closer to infinity; instead the total area approaches one-third.
A series whose sum approaches a finite number is said to be convergent. In contrast, a series whose sum does not approach any particular number is called divergent.
How do you know if a series will be convergent or divergent? In this Math Lab you will investigate the properties of series in order to identify them as convergent or divergent.
Materials
You will need a graphing calculator or graphing software.
Problem
How do you know if an infinite geometric series is convergent or divergent?
Procedure
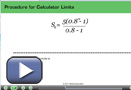
Watch Procedure for Calculator Limits to see how you should carry out the steps in this Math Lab. The procedure should be applied to each of the series given in the table.
Table
Complete a table like this one:
| Series | Standard Form | Common Ratio | Sn | Sum Limit |
| A | 2 + 6 + 18 + 54 + … | |||
| B | ||||
| C | 10 000 − 1000 + 100 − 10 + … | |||
| D | 0.6 − 4.2 + 29.4 − 205.8 + … |
Analysis
- Which series seemed to approach a number as the number of terms increased? Which ones did not approach any particular number?
- Review the pattern in the table. What property of a series can be used to separate geometric series that have a limit from geometric series that do not have a limit. Explain.
1.7. Explore 3
Module 1: Sequences and Series
Geometric Sum Limit
In the Math Lab you may have discovered the following points about infinite geometric series:
- when the common ratio is greater than 1 or less than −1, a limit to the sum does not exist (r > 1 or r < −1, no limit)
- when the common ratio is between −1 and 1, the sum of the series does have a limit (−1 < r < 1, limit)
Self-Check 1
Complete Geometric Series: Sum or No Sum.
Try This 2
In previous lessons you constructed formulas based on arithmetic and geometric patterns. You derived formulas by studying specific examples and combining formulas. In this activity you will determine a formula for evaluating the sum of an infinite geometric series where a sum exists.
- Choose any value for a common ratio, r, which would result in a convergent series.

- Evaluate r10, r20, r50, and r100 on your calculator. What do you notice about the value of rn as n increases? What number does rn approach as n gets larger?
- Substitute your result for rn from question 2 into the following formula:
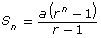
What does the expression for Sn begin to look like as n increases?
1.8. Explore 4
Module 1: Sequences and Series
Infinite Geometric Series Formula
In Try This 2 you may have discovered that for values between −1 and 1, the expression rn approaches zero as n increases. This causes the sum of a geometric-series expression to approach ![]() It is assumed that when n reaches infinity, the sum of the infinite geometric series will be
It is assumed that when n reaches infinity, the sum of the infinite geometric series will be ![]() By multiplying both the numerator and the denominator of this expression by −1, you get
By multiplying both the numerator and the denominator of this expression by −1, you get
![]()
If the sum of an increasingly greater number of terms in an infinite series approaches a finite number, this number is the sum of the infinite series.
Now is a good time to add the formula for the sum of an infinite geometric series to your copy of Formula Sheet.
Turn to “Example 1” on page 61 of the textbook to learn how you can evaluate an infinite geometric series using the formula you just derived. Pay attention to the notation used to show that a series is convergent. In part b., find out what would happen if you tried to apply the formula to a divergent series. At what point in the process will you realize that the infinite series cannot be evaluated?
1.9. Explore 5
Module 1: Sequences and Series
Try This 3
Retrieve your results from Try This 1. Your task in that activity was to determine the fraction of the original trapezoid that was shaded. You can now use the formula for evaluating the sum of an infinite geometric series to confirm your answer to that activity.
- Represent the shaded areas with the first few terms of an infinite series.
- Use the expression
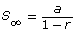 to evaluate the total shaded area. Does the answer confirm the result you obtained in Try This 1?
to evaluate the total shaded area. Does the answer confirm the result you obtained in Try This 1?
If your results do not match, return to your work in Try This 1. Retrace the steps you followed to determine the shaded area. You can try counting the number of grid triangles. Then divide this number by the total number of grid triangles in the original trapezoid.
![]() Make any necessary revisions to your work, and then save your work in your course folder.
Make any necessary revisions to your work, and then save your work in your course folder.
Self-Check 2
Complete Sum of Infinite Geometric Series.
There are many applications of infinite geometric series. One such application that is relevant to another area of math is converting repeating decimals into fractions.
Try This 4
- Write the number
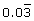 as an expanded number to 8 decimal places.
as an expanded number to 8 decimal places.
- Write this number as the sum of an infinite geometric series.

- Identify the first term and the common ratio for the series.
- Substitute the parameters into the infinite geometric series formula.
- Write an equivalent fraction for the expression in question 4. Check your answer by using a calculator to evaluate the fraction. Is the result the same as the original decimal?
- Describe how you would convert the decimal
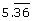 into a reduced fraction.
into a reduced fraction.
![]() Save your answers in your course folder.
Save your answers in your course folder.
Share 2
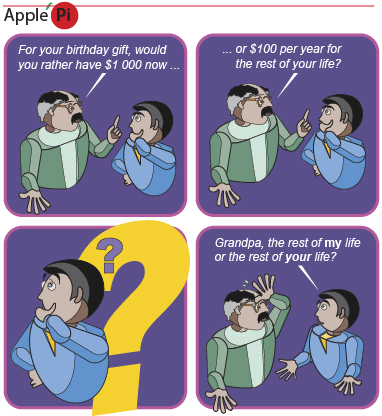
Another useful application of infinite geometric series is found in economics. If you were given the same choice as the boy in the cartoon, what would you choose?
With a classmate, discuss which option is better. Assume that the second option pays $100 at the end of each year. You may need more information before a decision can be made. Write down any additional questions that need to be asked. List one distinct advantage and one distinct disadvantage for each option. Based on your discussion, choose an option to support. Provide reasons to support your choice.
![]() Save your work in your course folder.
Save your work in your course folder.
Check with your teacher to see if you need to submit a copy for his or her review.
1.10. Explore 6
Module 1: Sequences and Series
Perpetuity
In the introduction to Explore, you learned that a perpetuity is a series of regular payments that last forever, much like the $100/yr option that the man offers his grandson in the cartoon. It may seem like a no-brainer to take a perpetuity of $100/yr as opposed to a one-time offer of $1000. After all, if you collect $100/yr for more than 10 yr, you will have more than $1000.
However, you need to consider the earning power of your money. Watch Perpetuities Explained to see the impact of investing your money.
Share 3
- The video explained how to determine the value of a perpetuity. With a classmate, discuss what you learned from the video. Ask any questions about parts of the presentation that you may not have fully understood.
- Answer the question posed at the end of the video. How much is a perpetuity of $100/yr worth?
- Revisit your responses from Share 2 and the question posed in the cartoon. Which one is the better option? Do you still stand by your original response? If you have changed your mind, why? Give reasons to support your answer.
![]() Save your work in your course folder.
Save your work in your course folder.
Did you know that some people borrow money to invest? This investment strategy makes sense as long as the interest paid on the investment is higher than the interest owed on the loan. The profit is the difference!
Self-Check 3
Complete questions 3, 12, 14, 16, and 18 on pages 63 and 64 of the textbook. Answer
1.11. Connect
Module 1: Sequences and Series
Open the Lesson 6 Assignment you saved in your course folder at the beginning of this lesson. Complete the assignment.
Project Connection
In this lesson you learned how infinite geometric series can be used to calculate the value of perpetuities. In your Module 1 Project you will interview someone who is retired. You will then begin to develop your own retirement plan.

© JJAVA/8861143/Fotolia
Go to Module 1 Project: Financing Your Dreams. Complete Project Connection 6: Retirement.
Going Beyond
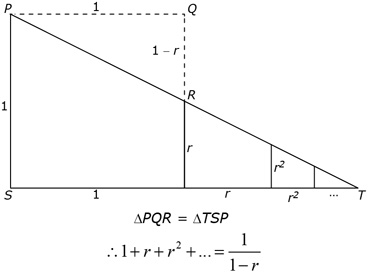
In mathematics, a proof is a series of statements that are logically related to one another and that, as a whole, establish the truth of a claim. The recreational mathematician and writer Martin Gardner once said the following:
There is no more effective aid in understanding certain [proofs] than a good diagram . . . . In many cases, a proof can be supplemented by a geometric analogue so simple and beautiful that the truth of a theorem is almost seen at a glance.
Source: Martin Gardner. “Mathematical Games,”
Scientific American, October 1973.
The diagram shown is an example of what Gardner was talking about. The diagram illustrates a proof of the formula for any infinite geometric series with a first term equal to 1. Note the two statements below the diagram. The first is a statement based on the diagram. The second is a natural outcome of the first statement.
Study the diagram. Describe the details of the proof.
- What is the logic behind the diagram?
- What does the first statement mean?

- How does the second statement follow from the first?
- How do the statements relate to the diagram?
Did You Know?
Recreational mathematics focus on the math underlying games and puzzles. Despite never taking any math course after high school, Martin Gardner maintained a deep interest in mathematics.

c 2.0 Mathematisches Forschungsinstitut Oberwolfach gGmbH – attribution - sharealike
Gardner was the author of the “Mathematical Games” column for the publication Scientific American for almost three decades. He wrote articles on topics such as flexagons, tangrams, cryptanalysis, and fractals. Did you know that fractals may be described as shapes whose properties can be described by geometric series?
Gardner passed away on May 22, 2010, at the age of 95.
Search the Internet for more “proofs without words.” You may find there are some very elegant ways of demonstrating a mathematical truth by using only a well-constructed diagram. Share your discoveries with classmates or your teacher.
![]() Save your work in your course folder.
Save your work in your course folder.
1.12. Lesson 6 Summary
Module 1: Sequences and Series
Lesson 6 Summary
In this lesson you investigated the following questions:
- When is it possible to add an infinite number of terms?
- How are infinite sums used in finance?
You investigated how the terms of an infinite geometric series could be added together. You discovered that, in some cases, adding an infinite number of terms does not result in a sum that increases without limit as the number of terms increases. In fact, by using applets and calculators you found that some sums approach a limit.
As more terms are added according to the geometric pattern in a series, rather than increasing without bound, the sum actually gets closer and closer to a finite number. This number is defined as the sum of that series.
If −1 < r < 1 for an infinite geometric series, its sum will exist and the series is considered convergent. On the other hand, if r > 1 or r < −1, the sum will not exist and the series is considered divergent.
Like finite geometric series, infinite geometric series have practical applications. You learned how to use the infinite geometric series formula to convert repeating decimals into reduced fractions.
A key application of infinite sums in the finance industry is in the computation of perpetuities. Infinite geometric series can be used to determine the present value of a perpetuity or a long-term annuity. This knowledge can help people make decisions about their investments and financial future.
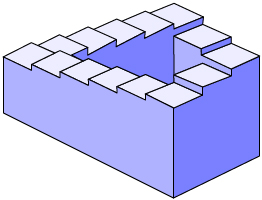
You investigated the concept of infinity and limits. The illustration of the never-ending staircase is an artistic example of the concept of infinity as being without end. You will continue to encounter these concepts in your future math courses, particularly if you study calculus.