Lesson 1
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-1 SS |
| Book: | Lesson 1 |
| Printed by: | Guest user |
| Date: | Thursday, 4 December 2025, 2:12 AM |
Description
Created by IMSreader
1. Lesson 1
Module 2: Trigonometry
Lesson 1: Foundations of Trigonometry
Focus

iStockphoto/Thinkstock
As mentioned in Module Introduction, trigonometry can be used to determine distances and angles when it is not feasible to measure them directly.
Stone arches in the shape of a semicircle are popular historic sites. Some of these are regularly repaired in order to preserve history. Repair of England’s Lune Aqueduct, similar to the arches pictured and first constructed in the 1700s, is currently planned. Measuring the heights at various angles inside the arches is an important part of the restoration. Later in this lesson you will see how trigonometry can help measure these heights.
In Lesson 1 you will learn about an extension of trigonometry that does not require right triangles and can be used for angles greater than 90°.
Outcomes
At the end of this lesson you will be able to
- describe how cosine, sine, and tangent are defined for angles greater than 90°
- determine the sign (positive or negative) of cosine, sine, and tangent for any angle without using your calculator
- state the number of solutions to a linear trigonometric equation, such as sin θ = 0.4
Lesson Questions
You will investigate the following questions:
- How can you use cosine, sine, and tangent for angles greater than 90°?
- How does the definition of cosine, sine, and tangent for angles greater than 90° affect the solution of equations?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 1 Assignment (Download the Lesson 1 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Module 2 Glossary Terms and Formula Sheet
- work under Project Connection
Self-Check activities are for your own use. You can compare your answers to suggested answers to see if you are on track. If you are having difficulty with concepts or calculations, contact your teacher.
1.1. Launch
Module 2: Trigonometry
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? This section, which includes Are You Ready? and Refresher, will help you find out.
Before beginning this lesson you should be able to
- understand and use the Pythagorean theorem (a2 + b2 = c2)
- understand and use the primary trigonometric ratios (SOH CAH TOA)
- understand the Cartesian plane, including coordinates of points and quadrants
1.2. Are You Ready?
Module 2: Trigonometry
Are You Ready?
Complete these questions. If you experience difficulty and need help, visit Refresher or contact your teacher.
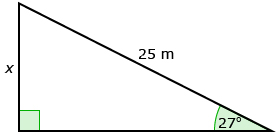
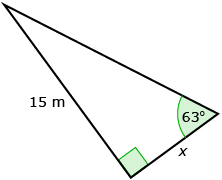
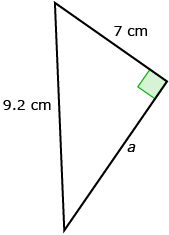
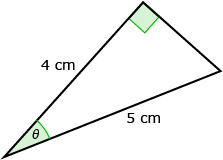
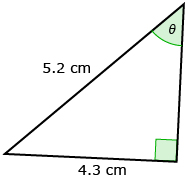
- Find the unknown length. State your answers rounded to the nearest tenth.
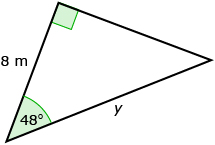
- Find the unknown angle. State your answers rounded to the nearest whole number.
- Locate the ordered pairs on the following grid.
- The Cartesian plane is divided into four quadrants. For each of the following, indicate the quadrant number in which the ordered pair is located.
How did the questions go? If you feel comfortable with the concepts covered in the questions, skip forward to Discover. If you experienced difficulties, use the resources in Refresher to review these important concepts before continuing through the lesson.
1.3. Refresher
Module 2: Trigonometry
Refresher
Review the use and meaning of the formula a2 + b2 = c2 in Pythagorean Theorem.
Print or save Primary Trigonometric Ratios Chart to review and keep handy.
Practise identifying the sides of a triangle by dragging and dropping the opposite, adjacent, and hypotenuse sides into their correct locations in Exploring Trigonometry.
Review examples of different types of trigonometry problems in Introduction to Trigonometry.
Review the four quadrants and the coordinates of a point on the plane in Cartesian Plane.
![]()
Your calculator must be set to degree mode for all calculations in Mathematics 20-1.
Just like there are different units of measure for distance (for example, kilometres and centimetres), there are different units of measure for angles (for example, degrees and radians). And just like you would get an incorrect answer if you used kilometres where centimetres were expected, you will get incorrect answers if you use radians or grads instead of degrees.
Have a look at your calculator screen. Typically, calculators will show “Deg,” “Rad,” or “Grad.” If your calculator shows “Deg,” it is in degree mode. If your calculator shows “Rad” or “Grad,” you need to press the Mode or DRG button until you see “Deg.”
If you cannot determine how to set your calculator to degree mode, you will need your calculator’s manual. These manuals can often be found on the Internet by entering your calculator’s make and model number into a search engine.
Go back to the Are You Ready? questions and try them again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 2: Trigonometry
Discover
In Try This 1 you will gain experience with different definitions for the primary trigonometric ratios. These definitions involve circles—not triangles! Since a circle has 360°, circles allow you to determine cosines, sines, and tangents of angles between 0° and 360°. The math that allows you to consider angles greater than 90° will be discussed later in this lesson. The goal right now is to get experience with this new approach to cosine and sine.
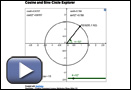
Try This 1
With a partner, use Cosine and Sine Circle Explorer to answer the questions below. The goal of Try This 1 is to get you thinking. Don’t worry if you can’t answer all of the questions.
There are two sliders you can use in this applet:
- Use the Radius slider (bottom left) to change the radius of the circle.
- Use the θ slider (bottom right) to change the angle shown. If you have trouble moving the slider precisely, click on the slider and use the arrow keys on your keyboard.
- As θ increases from 0° to 90°, sin θ increases from 0 to 1. What happens to sin θ as θ increases from 90° to 360°?
- What happens to cos θ as θ increases from 0° to 360°?
- Use the Radius slider to make the radius of the circle 1.0. Then examine the cosine and sine of different angles. Why is a radius of 1.0 special?

- Why does the equation cos θ = 0.2 have two solutions?
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.5. Explore
Module 2: Trigonometry
Explore
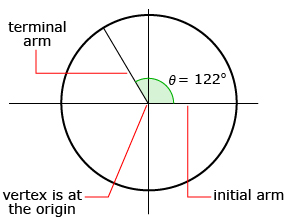
Try This 1 is based on an extended definition of cosine and sine that allows for any angle 0° ≤ θ ≤ 360°. ∠θ in Try This 1 is an example of an angle in standard position. Before going further, it is important to discuss angles in standard position.
Angles in standard position
- have their vertex at the origin (point (0, 0) on the Cartesian plane)
- are formed by an initial arm on the positive x-axis and a terminal arm
- are “swept out” in a counterclockwise direction from the initial arm to the terminal arm
![]() Save Module 2 Glossary Terms in your course folder now.
Save Module 2 Glossary Terms in your course folder now.
Here are some of the words you will want to define in Module 2 Glossary Terms in this lesson:
- standard position
- vertex
- initial arm
- terminal arm
- unit circle
1.6. Explore 2
Module 2: Trigonometry
Two Equal Heights on a Semicircle
Consider an engineer working on the Lune Aqueduct restoration project. The restoration of one of the semicircular arches with a radius of 5 m requires that anchors be installed. Installing the anchors requires using a special tool attached to a rotating boom. If the boom is positioned in the middle of the arch, at what angle must the boom rotate in a counterclockwise direction so that its endpoint is 4 m off the ground?
This situation can be modelled using a diagram.
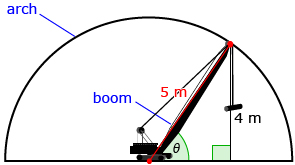
There is a second angle where the boom will be at a height of 4 m, as shown in the next diagram.
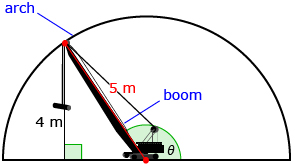
As you can see from the two diagram models, there are two places where the boom could be found 4 m above the ground. ∠θ could be within a right triangle (as in the first diagram) or outside a right triangle and greater than 90° (as in the second diagram).
If ∠θ is outside a right triangle, the trigonometry you learned in your last math course can’t be used to calculate the measure directly. ![]()
Self-Check 1
1.7. Explore 3
Module 2: Trigonometry
Formal Definitions for Primary Trigonometric Ratios
You are ready for the formal definition of the primary trigonometric ratios. Don’t worry that the definitions look different from what you learned with right triangles—you’ll soon see how the definitions are compatible with one another.
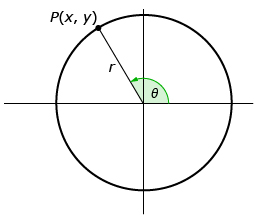
Given ∠θ drawn in standard position, with P being any point on the terminal arm, the primary trigonometric ratios are defined as follows:
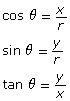
where
- x is the x-coordinate of point P.
- y is the y-coordinate of point P.
- r is the distance from the origin to point P (found by rearranging the Pythagorean formula
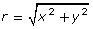 ).
).
![]()
Here is a way to help you remember that the definition for cosine uses the x-coordinate of P and the definition for sine uses the y-coordinate of P:
- Write x and y in alphabetical order and write cosine and sine in alphabetical order.
- x, y
- cosine, sine
- Both x and cosine come first, so the cosine definition involves the x-coordinate of P.
- Similarly, y and sine come second, so the sine definition involves the y-coordinate of P.
When P is on a circle of radius 1, these definitions simplify as follows:
cos θ = x ![]()
sin θ = y ![]()
![]()
![]()
Explore these definitions using Primary Trigonometric Ratios: Formal Definitions.
As you may have learned in Try This 1, some interesting facts can be seen using these definitions:
- When P is on a circle of radius 1, cosine and sine are simply, and respectively, the x- and y-coordinates of P.
- Equations of the form cos θ = k, where −1 ≤ k ≤ 1, usually have two solutions. The same is true for equations of the form sin θ = k and tan θ = k.
Note that these definitions only use circles—no triangles are required.
Remember that the cosine and sine of an angle are the coordinates of point P only if P is on a circle of radius 1. This is important to remember. Since the radius of the circle can be any value, the radius does not have to be 1.
The formal definitions for primary trigonometric ratios form the foundation of this module. Make sure you have added these formulas and any other information you think will be useful to your copy of Formula Sheet.
Self-Check 2
Use Primary Trigonometric Ratios: Formal Definitions to answer the following questions.
- Draw a right triangle in standard position with its terminal arm in quadrant 1.
- Write the tangent ratio you learned in your previous math course,
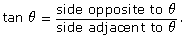
- The length of the side opposite to θ is the same as the y-coordinate of the endpoint of the terminal arm.
- The length of the side adjacent to θ is the same as the x-coordinate of the endpoint of the terminal arm.
- Replacing “side opposite to θ” to “y” and “side adjacent to x” with “y” results in the definition you learned in this lesson,
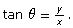
- Write the sine ratio you learned in your previous math course, SOH for

- The length of the side opposite to θ is the same as the y-coordinate of the endpoint of the terminal arm.
- The length of the hypotenuse is 1 since the hypotenuse is the radius of the circle.
Replacing “side opposite to θ” with “y” and “hypotenuse” with “1” results in the definition you learned in this lesson ![]()
- Write the cosine ratio you learned in your previous math course, CAH for
 .
.
- The length of the side adjacent to θ is the same as the x-coordinate of the endpoint of the terminal arm.
- The length of the hypotenuse is 1 since the hypotenuse is the radius of the circle.
Replacing “Side Adjacent to θ” with “x” and “hypotenuse” with “1” results in the definition you learned in this lesson ![]()
1.8. Explore 4
Module 2: Trigonometry
You may be wondering how the formal definitions of primary trigonometric ratios are different from what you learned about right triangles in previous math courses. You will investigate this question in Try This 2.
Try This 2
For angles between 0° and 90°, are the formal definitions for primary trigonometric ratios based on circles different from the definitions based on triangles?
SUMMARY OF PRIMARY TRIGONOMETRIC RATIO DEFINITIONS |
|
| Ratios Based on a Circle | Ratios Based on a Triangle |
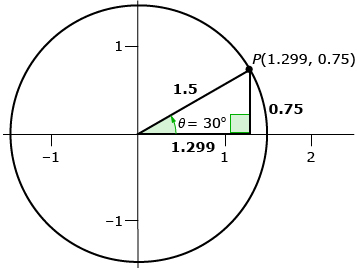
- Investigate the sine, cosine, and tangent of a 30° angle. Use the image of the triangle and Primary Trigonometric Ratios: Formal Definitions to complete a table like the following.
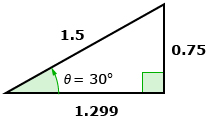
Trigonometric Function Trigonometric Ratio Based on a Triangle Trigonometric Ratio Based on a Circle
How do you know what length to make the circle radius?
sin 30° cos 30° tan 30° - How do the trigonometric ratios based on a circle and the ratios based on a triangle compare for sin 30°, cos 30°, and tan 30°?
- Explore this relationship further for other triangles using Relation to SOH CAH TOA. Add more rows to your table to record your observations.
- Do you think this relationship is true for other angles between 0° and 90°?
- Do you think this relationship is true for angles greater than 90°? Explain.
- Do you think this relationship is true for other angles between 0° and 90°?
![]() Save your responses in your course folder.
Save your responses in your course folder.
This triangle can also be drawn within a circle of radius 1.5. So, use a circle with a radius of 1.5.
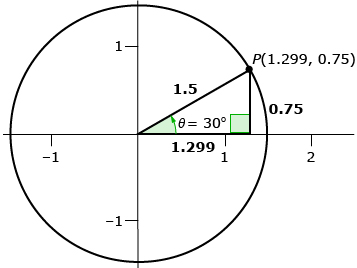
1.9. Explore 5
Module 2: Trigonometry
The Trigonometric Definitions Are Equivalent
As you may have noticed in Try This 2, the formal definitions for trigonometric ratios you’ve just been introduced to and the definitions you learned in your previous math courses (commonly remembered with SOH CAH TOA) are equivalent for angles 0° ≤ θ ≤ 90°.
You will get the exact same fractions whether you use a triangle with SOH CAH TOA or a circle with the same radius as the triangle’s hypotenuse and the new trigonometric definitions ![]() .
.
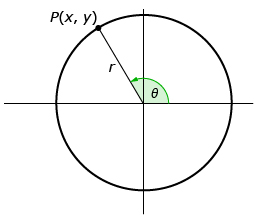
The definitions of the trigonometric ratios are identical because
- the side opposite to θ is always the same as the y-coordinate of point P
- the side adjacent to θ is always the same as the x-coordinate of point P
- the hypotenuse is always the same as the radius of the circle
With these new definitions of the primary trigonometric ratios, you can revisit the semicircle arch problem from Focus.
Example: Boom Angle

iStockphoto/Thinkstock
An engineer is working on the restoration of a semicircular arch with a radius of 5 m. As part of the repair, anchors must be installed at a height of 4 m using a special tool attached to a rotating boom. If the boom is positioned in the middle of the arch, at what angle must the boom rotate in a counterclockwise direction so the boom’s endpoint is 4 m off the ground?
Solution
You saw that there are two places where the boom could be found 4 m above the ground. ∠θ could be within a right triangle (as in the diagram on the left) or outside a right triangle and greater than 90° (as in the diagram on the right).
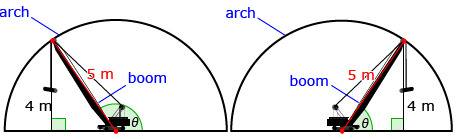
Because the new trigonometric definitions are based on a circle, you can show a slightly different diagram using the new definition for sine:
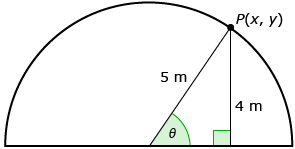
Using the circle-based definition for sine, the calculation is as follows:
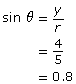
You know from this lesson that there are two solutions to this problem. In other words, there are two angles that make this situation true.
If you use Primary Trigonometric Ratios: Formal Definitions, you will find that the two values of θ that make this equation true are θ = 54° and θ = 126°. (These are approximate because the applet does not allow for exact solutions.) Check these angles using Primary Trigonometric Ratios: Formal Definitions.
1.10. Connect
Module 2: Trigonometry
Open your copy of Lesson 1 Assignment, which you saved in your course folder at the beginning of this lesson. Complete the assignment. Remember to show your work when completing assignments.
![]() Save all your work in your course folder.
Save all your work in your course folder.
Project Connection
At the end of Lesson 5 you will be prompted to complete Module 2 Project: Mars Rover Simulation, which is presented to you as a multimedia piece. As you work through the multimedia piece, you will collect information necessary to answer the questions in Module 2 Project Question Sheet.
You will need to conduct research in order to answer the first six questions. Conduct that research on the Internet or at the library now.
![]() Save all your work in your course folder.
Save all your work in your course folder.
Going Beyond

© jeff gynane/184206/Fotolia
A beautiful rose window completed in intricate stained glass! A rose window is a circular window found in the major Gothic cathedrals of Northern France. The window illustrated is found in Paris’ Notre Dame Cathedral, which was constructed in the medieval period. The construction of such windows has an interesting connection to your current study of trigonometry.

iStockphoto/Thinkstock
Using your knowledge of angles from 0° to 360°, can you figure out how students from an Alberta Mathematics 20 classroom created artwork similar to rose windows?
1.11. Lesson 1 Summary
Module 2: Trigonometry
Lesson 1 Summary
In this lesson you investigated the following questions:
- How can you use cosine, sine, and tangent for angles greater than 90°?
- How does the definition of cosine, sine, and tangent for angles greater than 90° affect the solution of equations?
You learned the formal definitions for the primary trigonometric ratios.
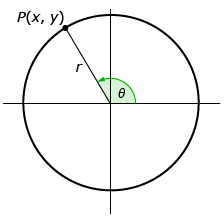
If given ∠θ drawn in standard position, with P being any point (x, y) on the terminal arm, the primary trigonometric ratios are defined as follows:
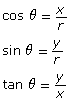
where
- x is the x-coordinate of point P
- y is the y-coordinate of point P
- r is the distance from the origin to point P
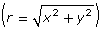
These new definitions are compatible with the right-triangle definitions you learned in your last math course. These definitions allow the use of angles greater than 90°. In Mathematics 20-1 you will only deal with 0° ≤ θ ≤ 360°; however, the formal definitions are valid for any angle.
This definition creates two interesting results (which you will use in Lessons 2 and 3):
- When P is on a circle of radius 1, cosine and sine are simply, and respectively, the x- and y-coordinates of P.
- Equations like cos θ = 0.2 usually have two solutions (similarly for sine and tangent).
In Lesson 2 you will learn how to solve equations like this algebraically rather than by using Primary Trigonometric Ratios: Formal Definitions.