Lesson 2
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-1 SS |
| Book: | Lesson 2 |
| Printed by: | Guest user |
| Date: | Thursday, 4 December 2025, 2:08 AM |
Description
Created by IMSreader
1. Lesson 2
Module 2: Trigonometry
Lesson 2: Solving Linear Trigonometric Equations
Focus

Calgary tower: Photodisc/Thinkstock; Tower of Pisa: AbleStock.com/Thinkstock
As shown with the semicircular arches, architecture makes extensive use of symmetry. Some of the world’s more impressive buildings are based on circle geometry. The Calgary Tower and the Leaning Tower of Pisa are significantly based on circle symmetry—the same symmetry you’re using to study trigonometry.
The circle symmetry in the Calgary Tower makes the Tower’s famous revolving restaurant possible. Circle symmetry also makes the structure resistant to earthquakes and strong winds. The Tower of Pisa could be seen as circle symmetry gone wrong. On closer examination, however, the symmetry is sound—an engineering error causes the tilt. The fact that the Leaning Tower of Pisa stands nearly 1000 years after construction was started speaks to the strength of the circle.
In Lesson 1 you used Primary Trigonometric Ratios: Formal Definitions to determine the two angles at which a boom repairing a semicircular arch would be 4 m above the ground. The equation to be solved was sin θ = 0.8. In Lesson 2 you will learn to use your calculator and symmetry to solve equations like these.
Outcomes
At the end of this lesson you will be able to
- explain how symmetry can be used to solve equations of the form sin θ = k, where −1 ≤ k ≤ 1
- solve equations of the form sin θ = k, where −1 ≤ k ≤ 1 (for each of sine, cosine, and tangent)
Lesson Question
In this lesson you will investigate the following question:
- How does circle symmetry help solve equations of the form sin θ = k, where −1 ≤ k ≤ 1?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 2 Assignment (Download the Lesson 2 Assignment and save it in your course folder now.)
- course folder submissions from Math Lab, Try This, and Share activities
- additions to Module 2 Glossary Terms and Formula Sheet
Materials
You will need the following supplies:
- three copies of Circle of Angles
- a pencil
- a ruler
1.1. Discover
Module 2: Trigonometry
Discover
In Lesson 1 you used the applet Primary Trigonometric Ratios: Formal Definitions to solve equations like cos θ = 0.7. You found that there were always two answers to this equation. In previous math courses you may have found one solution to this by writing θ = cos−1(0.7) then entering cos−1(0.7) into your calculator to get the answer 46°. How do you get the second solution (314°) without having to use the applet Primary Trigonometric Ratios: Formal Definitions?
In Try This 1 you will explore the relationship between the answer given by your calculator and the second answer given by the applet.
Try This 1
Print three copies of Circle of Angles. You will use one copy in each part of Try This 1. Do you prefer to work digitally? If so, you can paste a screenshot of Circle of Angles into a drawing program on your computer.
You will be using Primary Trigonometric Ratios: Formal Definitions, which you first used in Lesson 1.
Part 1
Step 1: Use Primary Trigonometric Ratios: Formal Definitions to determine the two values of θ that make the equation cos θ = 0.309 true.
Step 2: Draw these two angles in standard position on one of the Circle of Angles worksheets you printed. Mark a large point where each terminal arm intersects the circle. ![]()
Step 3: Fold the worksheet along the thick horizontal line (the x-axis). Record what you notice, if anything, about the two points on the terminal arms.
Step 4: Fold the worksheet along the thick vertical line (the y-axis). Record what you notice, if anything, about the two points on the terminal arms.
Repeat Steps 1 to 4 for the following equations.
- cos θ = 0.9135
- cos θ = −0.6691
- cos θ = −0.9976
Part 2
Step 1: Use Primary Trigonometric Ratios: Formal Definitions to determine the two values of θ that make the equation sin θ = 0.4695 true.
Step 2: Draw these two angles in standard position on the second Circle of Angles worksheet you printed. Mark a large point where each terminal arm intersects the circle.
Step 3: Fold the sheet along the thick horizontal line (the x-axis). Record what you notice, if anything, about the two points on the terminal arms.
Step 4: Fold the sheet along the thick vertical line (the y-axis). Record what you notice, if anything, about the two points on the terminal arms.
Repeat Steps 1 to 4 for the following equations:
- sin θ = 0.9613
- sin θ = −0.9272
- sin θ = −0.4384
Part 3
Step 1: Use Primary Trigonometric Ratios: Formal Definitions to determine the two values of θ that make the equation tan θ = 1.8807 true.
Step 2: Draw these two angles in standard position on the third Circle of Angles worksheet you printed. Mark a large point where the terminal arms intersect the circle.
Step 3: Fold the sheet along the thick horizontal line (the x-axis). Record what you notice, if anything, about the two points on the terminal arms.
Step 4: Fold the sheet along the thick vertical line (the y-axis). Record what you notice, if anything, about the two points on the terminal arms.
Repeat Steps 1 to 4 for the following equations:
- tan θ = 0.364
- tan θ = −0.2126
- tan θ = −2.4751
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 1
For each part of Try This 1, discuss the following questions with a partner or group.
- Does there appear to be a pattern to the relationship between each pair of angles you plotted?
- Can you see any relationship between the patterns you identified in Try This 1 and the primary trigonometric ratios introduced in Lesson 1?
![]() Save a summary of the patterns and relationships you discussed in your course folder.
Save a summary of the patterns and relationships you discussed in your course folder.
You will refer to your notes in Explore.
Your sheet will look similar to this:
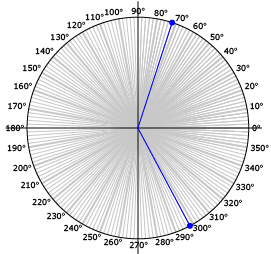
1.2. Explore
Module 2: Trigonometry
Explore
In Try This 1 you worked through three activities to identify some patterns for finding the solutions to equations in the form cos θ = k; sin θ = k, where −1 ≤ k ≤ 1; and tan θ = a, ![]() . In Try This 2 you will identify and confirm the patterns you may have noticed in Try This 1.
. In Try This 2 you will identify and confirm the patterns you may have noticed in Try This 1.
Try This 2
- Work through Cosine Reflection Equation to help you identify methods for finding solutions to equations of the form cos θ = k, where −1 ≤ k ≤ 1.
- Work through Sine Reflection Equation to help you identify methods for finding solutions to equations of the form sin θ = k, where −1 ≤ k ≤ 1.
- Work through Tangent Reflection Equation to help you identify methods for finding solutions to equations of the form tan θ = a,
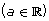 .
.
- Look back at the patterns you described in Share 1. How do they compare with the patterns you observed in the animations above?
- Summarize your observations by creating three general rules that describe the relationship between the axis of reflection of the two solutions for cos θ = k, sin θ = k (−1 ≤ k ≤ 1), and tan θ = a,
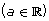 .
.
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.3. Explore 2
Module 2: Trigonometry
The Relationship Between the Solutions and the Axis of Reflection
In Try This 2 you developed three general rules to describe the relationship between the solutions for cos θ = k, sin θ = k (−1 ≤ k ≤ 1), and the axis of reflection. Compare the rules you developed to the following rules.
Cosine Equations
- The terminal arms of the two solutions to equations of the form cos θ = k, where −1 ≤ k ≤ 1, are always reflections of each other in the x-axis.
Sine Equations
- The two solutions to equations of the form sin θ = k, where −1 ≤ k ≤ 1, are always reflections of each other in the y-axis.
Tangent Equations
- The two solutions to equations of the form tan (θ) = a, (a ∈
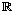 ) are always reflections of each other in both the x-axis and the y-axis. This always results in the two terminal arms forming a straight line.
) are always reflections of each other in both the x-axis and the y-axis. This always results in the two terminal arms forming a straight line.
Here is a way to help you remember which trigonometric ratio is reflected in which axis:
- The definition for cosine involves the x-coordinate of the endpoint of the terminal arm P(x, y),
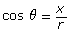 . The second solution of an equation like cos θ = k is a reflection in the x-axis.
. The second solution of an equation like cos θ = k is a reflection in the x-axis.
- The definition for sine involves the y-coordinate of the endpoint of the terminal arm P(x, y),
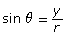 . The second solution of an equation like sin θ = k is a reflection in the y-axis.
. The second solution of an equation like sin θ = k is a reflection in the y-axis.
- The definition for tan involves both the x- and y-coordinates of the endpoint of the terminal arm P(x, y),
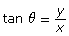 . The second solution to an equation like tan θ = k is a reflection in both the x- and y-axes.
. The second solution to an equation like tan θ = k is a reflection in both the x- and y-axes.
The solution method for equations of the form cos θ = k, where −1 ≤ k ≤ 1, used in this resource is significantly different from the method shown in the textbook. Be aware that other strategies exist but that the Self-Check activities in this lesson reflect the solution method presented in this resource.
The relationships described in this section can be used to solve linear trigonometric equations. The next examples illustrate an approach using this knowledge.
1.4. Explore 3
Module 2: Trigonometry
Example 1: Equations of the Form cos θ = k, Where −1 ≤ k ≤ 1
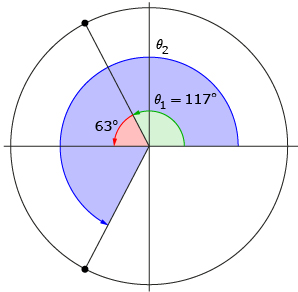
Nasreen has been asked to solve the equation cos θ = −0.45 to the nearest degree. She knows that there must be two solutions to this equation.
Solution
Step 1: Nasreen determines the first solution by entering cos−1(−0.45) in her calculator and rounds it to the nearest degree.

Step 2: She sketches the angle given by her calculator (117°).
She knows that the terminal arm of the second solution, θ2, must be a reflection in the x-axis of θ1’s terminal arm. Therefore, she sketches θ2 with its terminal arm in quadrant 3.
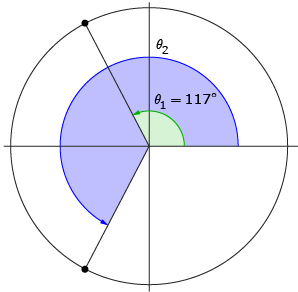
Step 3: Nasreen knows that a straight line is an angle of 180°; thus, the angle between θ1’s terminal arm and the x-axis must be 180° − 117° = 63°.
Step 4: Because the terminal arm of θ2 is a reflection in the x-axis of θ1’s terminal arm, Nasreen knows the angle between the x-axis and θ2’s terminal arm must also be 63°.
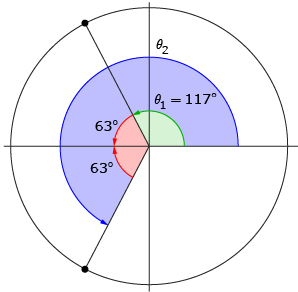
Step 5: Nasreen determines the second solution:
θ2 = 117° + 63° + 63° = 243°
The two solutions to the equation cos θ = −0.45 are θ1 = 117° and θ2 = 243°.
1.5. Explore 4
Module 2: Trigonometry
Example 2: Equations of the Form sin θ = k, Where −1 ≤ k ≤ 1
David has been asked to solve the equation sin θ = −0.61 to the nearest degree. He knows there must be two solutions to this equation.
Step 1: David determines the first solution by entering sin−1(−0.61) in his calculator and rounds the answer to the nearest degree.
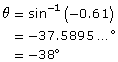
Step 2: How can an angle be negative?
In the context of angles in standard position, negative angles correspond to rotations in the clockwise direction. (Up until now, you’ve been dealing with rotations in the counterclockwise direction).
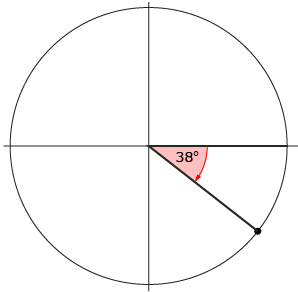
Mathematically, there is nothing wrong with negative angles. However, in the context of Mathematics 20-1, angles are always expressed in their equivalent positive form.
Since an angle that is a full revolution is 360°, David concludes that an angle of −38° is equivalent to an angle of 360° − 38° = 322°.
David sketches this angle, calling it θ1.
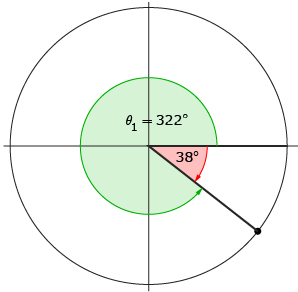
Step 3: He knows that the terminal arm of the second solution, θ2, must be a reflection in the y-axis of θ1’s terminal arm. Therefore, he sketches θ2 with its terminal arm in quadrant 3.
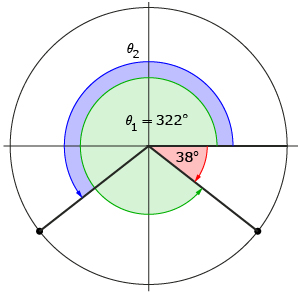
Step 4: Because the terminal arm of θ2 is a reflection in the y-axis of θ1’s terminal arm, David knows the angle between the x-axis and θ2’s angle must also be 38°.
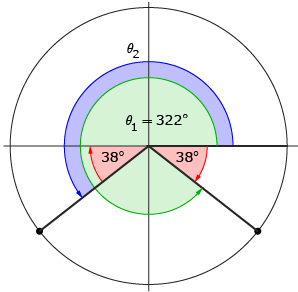
Step 5: David knows that a straight line is an angle of 180° and uses this to determine the second solution:
θ2 = 180° + 38° = 218°
The two solutions to the equation sin θ = −0.61 are θ1 = 322° and θ2 = 218°.
1.6. Explore 5
Module 2: Trigonometry
Self-Check 1
- Determine the two solutions to the equation cos θ = 0.27 rounded to the nearest degree. Explain each step in the process. Answer
- Solve the equation sin θ = 0.86 to the nearest degree. Explain each step in the process. Answer
- Solve the equation tan θ = 4.01 to the nearest degree. Explain each step in the process. Answer
- For each of the following equations, sketch a diagram with all appropriate angles labelled and determine the solutions.
- The equation sin θ = 1 has only one solution. State the solution and explain why there are not two solutions. Answer
- Solve the following equations.
1.7. Connect
Module 2: Trigonometry
Open the Lesson 2 Assignment you saved in your course folder at the start of this lesson. Complete the assignment.
![]() Save all your work in your course folder.
Save all your work in your course folder.
Going Beyond

Hemera/Thinkstock
You have likely heard of cloud computing and how it is likely to change the way you work with word processing, spreadsheets, graphics, and many other applications. A new style of forum, called the circle cloud forum, has also recently emerged. The roots of this way of working is found in circle talk, an important part of the First Nations’ culture.
In a First Nations’ circle talk, a talking stick is passed around. Only the person holding the talking stick can speak. A circle is a whole made up of equally valuable parts. Everyone is the same distance from the middle of the circle, so there is no sense of hierarchy. The point of reference changes as each person speaks. The circle helps make everyone a part of a community of equals striving for sharing and understanding.
You may wish to use an Internet search engine to learn more about this interesting feature of a circle as a metaphor for human connection.
1.8. Lesson 2 Summary
Module 2: Trigonometry
Lesson 2 Summary
In this lesson you learned that, with the exception of sin θ = ±1 and cos θ = −1, all equations of the form cos θ = k, where −1 ≤ k ≤ 1, have two solutions when angles are limited to 0° ≤ θ ≤ 360°.
You learned about each type of equation.
Sine: sin θ = k, where −1 ≤ k ≤ 1
- The first solution, θ1, can be obtained by entering sin−1(k) in your calculator.
- The second solution will have a terminal arm that is a reflection in the y-axis of θ1’s terminal arm.
- Your calculator may give you a negative angle. This negative angle corresponds to a clockwise rotation and can be converted to a positive angle using 360° − θ1.
Cosine: cos θ = k, where −1 ≤ k ≤ 1
- The first solution, θ1, can be obtained by entering cos−1(k) in your calculator.
- The second solution will have a terminal arm that is a reflection in the x-axis of θ1’s terminal arm.
Tangent: tan θ = a, a ∈ ![]()
- The first solution, θ1, can be obtained by entering tan−1(k) in your calculator.
- The second solution will have a terminal arm that is a reflection in the x-axis and y-axis of θ1’s terminal arm. As a result, the two terminal arms form a straight line.
In all cases, circle symmetry was used to determine the second solution.



