Lesson 3
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-1 SS |
| Book: | Lesson 3 |
| Printed by: | Guest user |
| Date: | Thursday, 4 December 2025, 2:08 AM |
Description
Created by IMSreader
1. Lesson 3
Module 2: Trigonometry
Lesson 3: Trigonometry Without Technology
Focus

Hemera/Thinkstock
Bridges have always been needed to cross rivers and ravines. Bridges require sturdy trusses. The exact origin of the truss web, made up of identical repeating triangles, is unclear. Today, many other types of trusses exist. Triangles are one element all the different types of trusses have in common. You probably don’t have to look hard to see the triangles that make up the truss bridge shown in the photo.
In 1848, James Warren obtained a British patent for a design of repetitive equilateral triangles that could support a roadbed on either its top or bottom dimension. Warren's name became synonymous with this form of truss design.
How did the mathematicians and engineers who worked on bridges solve trigonometric equations without calculators? The vast majority of them used tables of values. One of the oldest known tables of values was created by the Greek astronomer and mathematician Hipparchus (ca. 190 BC to 120 BC). How were those tables created?
This lesson will help you understand how to calculate the cosine, sine, or tangent of a number of special angles without a calculator.
Outcomes
At the end of this lesson you will be able to
- determine, without the use of technology, the cosine, sine, or tangent of 0°, 30°, 45°, 60°, and 90° angles, and their reflections in the other three quadrants of the Cartesian plane
- determine the cosine, sine, or tangent of angles given the coordinates of a point on the terminal arm
Lesson Question
You will investigate the following question:
- How can the cosine, sine, or tangent of an angle be determined without technology?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 3 Assignment (Download the Lesson 3 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Module 2 Glossary Terms and Formula Sheet
1.1. Discover
Module 2: Trigonometry
Discover
Consider the following circle of radius 2 units.
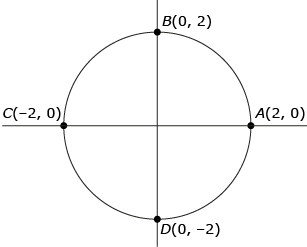
One could imagine superimposing angles in standard position on top of this circle. For instance, this is what a 180° angle would look like:
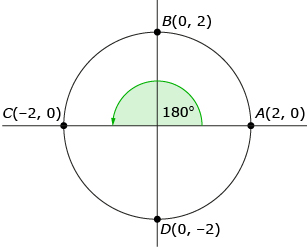
Since you know the coordinates of a point on the terminal arm and the distance from that point to the origin (r), you can determine the cosine, sine, and tangent of 180° without technology by using the definitions introduced in Lesson 1.
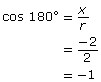 |
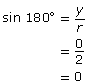 |
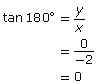 |
Try This 1
Use the definitions process to determine the cosine, sine, and tangent of the following angles.
| θ | cos θ | sin θ | tan θ |
| 0° | |||
| 90° | |||
| 180° | −1 | 0 | 0 |
270° |
|||
| 360° |
![]() Save your chart in your course folder.
Save your chart in your course folder.
Share 1
Compare your results with a partner.
- Discuss any differences and try to come to agreement on all values in the table.
- How would your values change if the circle had been drawn with a radius of 3 or with any other radius?
![]() If required, save a copy of your discussion in your course folder.
If required, save a copy of your discussion in your course folder.
1.2. Explore
Module 2: Trigonometry
Explore
In Discover you determined the cosine, sine, and tangent for 0°, 90°, 180°, 270°, and 360° angles using points on a circle with a radius of 2. In Share 1 you may have discussed the fact that the values for these trigonometric ratios are always the same and don’t depend on the radius of the circle.
Finding the trigonometric ratios for these angles was straightforward because the terminal arms of each angle landed on either the x- or y-axis, making the point P(x, y) easily known. But what about other angles whose terminal arms do not lie on the x- or y-axis?
You already saved Module 2 Glossary Terms in your course folder. In this lesson you will define the following terms, and maybe others, in your copy of Module 2 Glossary Terms:
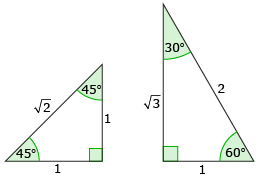
- 45-45-90 special triangle
- 30-60-90 special triangle
In the following activities you will investigate special triangles and explore how they can help identify trigonometric ratios for angles that do not lie on the x- or y-axis.
Try This 2
Follow the steps and answer the questions.
Step 1: Consider a square of side length 1 unit.
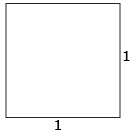
Step 2: When a diagonal is drawn in the square, what are the angles θ1 and θ2? ![]()
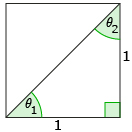
Step 3: The diagonal splits the square into two right triangles. What is the length of the hypotenuse? ![]()
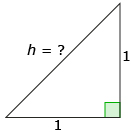
Step 4: Your diagram should now look like this:
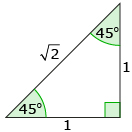
Step 5: Use this triangle to determine cos 45°, sin 45°, and tan 45°. ![]()
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.3. Explore 2
Module 2: Trigonometry
Using Special Triangles to Find Angles
In Try This 2 you saw how cosine, sine, and tangent can be determined for a 45° angle without using technology. Watch Finding Trigonometric Ratios for 30° and 60° Angles Without Technology.
You can now create a very basic table of trigonometric values based on the ratios found using
- angles with terminal arms that lie on the x- or y-axis of a circle (0°, 90°, 180°, 270°, and 360°)
- angles found in special triangles (30°, 45°, 60°)
| θ | cos θ | sin θ | tan θ |
| 0° | 1 | 0 | 0 |
| 30° | |||
| 45° | 1 | ||
| 60° | |||
| 90° | 0 | 1 | undefined |
| 180° | −1 | 0 | 0 |
| 270° | 0 | −1 | undefined |
| 360° | 1 | 0 | 0 |
So far you have used these special triangles only for angles in the first quadrant (0° ≤ θ ≤ 90°). These triangles can be used to find angles in other quadrants too. The key is to use one of these special triangles to determine the coordinates of a point on the terminal arm of the angle in question. Watch Using a 30-60-90 Triangle for a 150° Angle.
Sometimes it’s not as obvious to see how to use one of the special triangles. Watch Using a 30-60-90 Triangle for a 300° Angle to see how a similar process can be used for a 300° angle.
1.4. Explore 3
Module 2: Trigonometry
Special Angles Around a Circle
Recall the question posed in Focus. Historically, how did mathematicians and engineers solve trigonometric equations without calculators or other forms of modern technology? The answer is that they used special triangles!
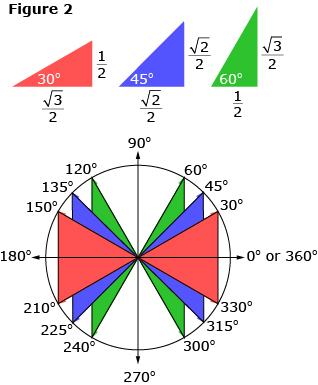
These two special triangles (45-45-90 and 30-60-90) were used by trigonometric table makers to determine the exact trigonometric values for all the angles shown in the diagram.
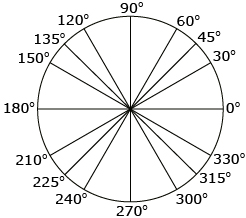
Other techniques, including trigonometric identities, were used to add more angles to their tables. These developments will be discussed in Mathematics 30-1.
For convenience, you often use a calculator to find the sine, cosine, or tangent of an angle. The resulting answer is often given as a decimal, which is an approximation of the value rather than the exact answer. For some special angles, you can find the exact answer as a fraction or a radical.
Take, for example, cos (30°) = 0.866 025 403. This is an approximation to cos (30°). The exact value can be found using the special triangle and is ![]() which is not a finite decimal.
which is not a finite decimal.
You can find the exact value when the angle is 30°, 45°, or 60°.
Self-Check 1
1.5. Explore 4
Module 2: Trigonometry
Finding Angles from a Point on the Terminal Arm
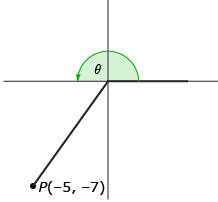
In Try This 1 you were given the coordinates of endpoints on terminal arms of 0°, 90°, 180°, 270°, and 360° angles and asked to determine the cosine, sine, and tangent of these angles. This process can be extended to other angles where a point on the terminal arm of the angle is known. Consider the following example.
Point P(−2, 3) is on the terminal arm of an unknown angle, θ. Determine the exact values for cos θ, sin θ, and tan θ.
The first step is to draw a picture.
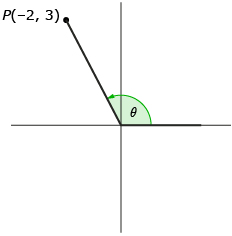
Recalling the primary trigonometric ratio definitions, you can write the following ratios:
The only piece missing is r, the distance from the origin to P(−2, 3). This can be determined by imagining that the terminal arm is the hypotenuse of a right triangle.
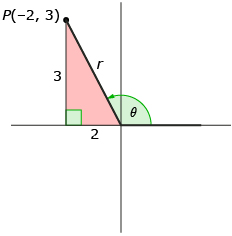
The Pythagorean theorem can be used to determine r.
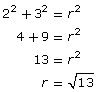
The primary trigonometric ratios of this angle can now be written in full.
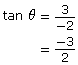 |
Note that ![]() and
and ![]() are mathematically equivalent. By convention, the negative sign is normally written with the numerator.
are mathematically equivalent. By convention, the negative sign is normally written with the numerator.
Self-Check 2
Complete questions 3, 8.a., and 8.c. on page 96; and question 13 on page 84 of the textbook. Answers
1.6. Connect
Module 2: Trigonometry
Open your copy of the Lesson 3 Assignment, which you saved in your course folder at the start of this lesson. Complete the assignment.
![]() Save all your work in your course folder.
Save all your work in your course folder.
Going Beyond
Geodesic domes are elegant and sophisticated structures. They are lightweight, extremely strong, and earthquake proof, and these domes make an efficient use of materials. Domes are ideal structures to create unobstructed internal space or for their use in challenging building sites, like the Arctic. If you look carefully at the photographs, you will likely notice triangles are once again a major component of the design.

clear dome: iStockphoto/Thinkstock; white dome: iStockphoto/Thinkstock
The construction of these domes uses spherical trigonometry to figure out the angles at which triangles are joined to create the three-dimensional spherical structure in a geodesic dome. You may want to further investigate spherical trigonometry and this unique type of construction.
1.7. Lesson 3 Summary
Module 2: Trigonometry
Lesson 3 Summary
In this lesson you investigated the following question:
- How can the cosine, sine, or tangent of an angle be determined without technology?
You learned how to determine the side lengths of 30-60-90 and 45-45-90 special triangles and how using triangles can be used to determine the cosine, sine, and tangent for each of the following angles.
You also learned how to determine the exact values of cosine, sine, and tangent in situations where you only know the coordinates of a point on the terminal arm.
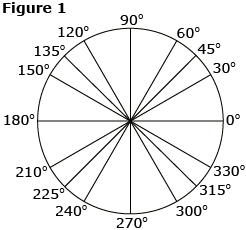
You don’t have to memorize the exact values for cosine, sine, and tangent for all sixteen angles shown in Figure 1.
- The values for 0°, 90°, 180°, 270°, and 360° can be easily determined using the coordinates of any point on their terminal arms.
- The values for 30°, 45°, and 60° can be determined using the special triangles shown above.
- All other values can be determined by using either 45-45-90 or 30-60-90 special triangles.
Another way to remember the ratios is to remember the red, blue, and green triangles.
The special triangles, 30-60-90 and 45-45-90, can be drawn in the unit circle, as shown in Figure 2. Knowing the ratios of the special triangles will determine the exact value of sin θ and cos θ and thus the x- and y-coordinates that lie on the edge of the circle.