Lesson 4
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-1 SS |
| Book: | Lesson 4 |
| Printed by: | Guest user |
| Date: | Thursday, 4 December 2025, 2:15 AM |
Description
Created by IMSreader
1. Lesson 4
Module 2: Trigonometry
Lesson 4: The Sine Law
Focus
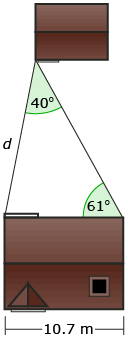
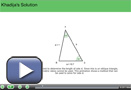
Khadija is building a walkway from her back door to her shed, which is located at the back of the yard. She needs to provide the length to a contractor in order to get a phone estimate for the cost of building the walkway. She knows her house is 10.7-m wide, and she has measured two angles as shown in the diagram.
How would you solve this problem to find the distance? In previous math courses, you solved triangle problems that involved right triangles—or triangles that had a 90° angle. But what about non-right triangles, as shown in this scenario?
There is a triangle in this problem, but it is not a right triangle. So, the primary trigonometric ratios cannot be used. In this lesson you will investigate the sine law, which can be used for oblique triangles.
Outcomes
At the end of this lesson you will be able to
- use the sine law to solve for sides or angles in oblique triangles
- determine how many solutions are possible in a situation called the ambiguous case with the sine law
Lesson Questions
You will investigate the following questions:
- How can angles and sides in any triangle—oblique and right—be found?
- How does your knowledge of solutions to equations of the form sin θ = k (from Lessons 1 and 2) affect solutions using the sine law?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 4 Assignment (Download the Lesson 4 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Module 2 Glossary Terms and Formula Sheet
1.1. Discover
Module 2: Trigonometry
Discover
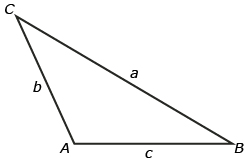
The math in this lesson relies on a standard way of labelling triangles:
- Sides are named with lowercase letters.
- Angles are named with uppercase letters.
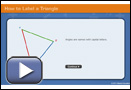
Sides and their opposite angles are named with the same letter (for example, side b and ∠B are opposite each other). The animation How to Label a Triangle shows this naming convention in more detail.
Watch Khadija’s Solution to see a way to create and use right triangles to solve Khadija’s problem.
Share 1
With a partner, discuss and try to agree on the answers to the following questions. The goal of Share 1 is to get you thinking; don’t worry if you can’t answer all the questions.
At the end of the animation, Khadija concludes with the equation ![]()
- What, if anything, would change if Khadija’s triangle had the measurements a = 6, ∠A = 52°, and ∠D = 53°?
- What, if anything, would change if Khadija’s triangle had the measurements a = 15.2, ∠A = 63°, and ∠D = 46°?
- Is there any conclusion you can draw from your answers to questions 1 and 2? Explain.
Try This 1
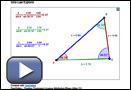
Khadija concluded with an equation involving ratios of sines: ![]() The applet Sine Law Explorer also shows ratios involving sines. In Sine Law Explorer, drag the points of the triangle to change the measure of the angles and lengths of sides. Observe what happens to the ratios.
The applet Sine Law Explorer also shows ratios involving sines. In Sine Law Explorer, drag the points of the triangle to change the measure of the angles and lengths of sides. Observe what happens to the ratios.
Share 2
Compare your observations with a partner. With your partner, describe an equation or relationship that appears to be true for all triangles.
![]() Place a copy of your conclusion in your course folder. Your teacher may ask to see your conclusion later.
Place a copy of your conclusion in your course folder. Your teacher may ask to see your conclusion later.
1.2. Explore
Module 2: Trigonometry
Explore
The relationship you discovered in Try This 1 is called the sine law and is valid for all triangles—both right triangles and oblique triangles. The sine law is usually written in the following way:
The sine law can also be written as three separate equations:
This mathematical expression can be expressed in words as follows:
The length of a side divided by the sine of the opposite angle is the same for all side-angle pairs in any triangle. |
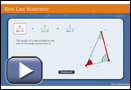
Watch Sine Law Illustrator to see the sine law explained.
Add the formula for the sine law to your copy of Formula Sheet.
1.3. Explore 2
Module 2: Trigonometry
Using the Sine Law to Solve for Distance

iStockphoto/Thinkstock
This is a photo of a trig point at Old Man of Coniston in England.
The sine law is valid for all triangles, but the law is especially useful for oblique triangles. This is because the sine law is the first formula you have encountered that is valid for oblique triangles and not all problems involve right triangles.
Trigonometry using oblique triangles was important in the early twentieth century when the British government wanted its maps (based on survey work done between 1783 and 1853) to be more accurate. The triangulation method of surveying was used to complete the Retriangulation of Britain between 1935 and 1962.
Concrete pillars called trig points were created all around the country. These pillars became the vertices of triangles that were used to create accurate maps of Britain. Trigonometry played an important role in helping to calculate the angles and distances between trig points.
Example 1: Lake Claire
Today, if you were to use triangulation to measure distances around Lake Claire in northeast Alberta, you might end up with trig points and corresponding triangles in the locations shown in the diagram.
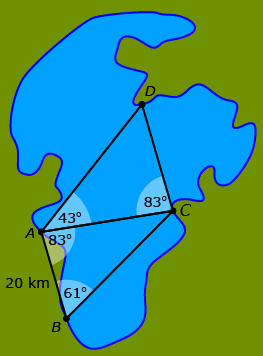
The sine law could be used to determine all the unknown distances. The following steps show the calculation of the distance across the lake, ![]() using
using ![]()
![]() is the only known side. Thus, to use the sine law, the angle opposite
is the only known side. Thus, to use the sine law, the angle opposite ![]() must be calculated.
must be calculated.
Write the sine law using a side-angle pair that you know and the side-angle pair with your unknown distance.
![]()
Multiply both sides by sin 61° in order to isolate ![]()
![]()
Cancel sin 61° to isolate ![]()
![]()
![]() = 29.7598…
= 29.7598…
Unless stated otherwise, distances should be rounded to the nearest tenth.
![]() = 29.8 km
= 29.8 km
Canada’s First Nations people were the first map makers in Canada. Undoubtedly, their maps were useful to the early European explorers in what would become Canada. However, these maps had two significant differences to what the Europeans would have been used to:
- The First Nations’ maps were usually memorized and only drawn when required to communicate locations and distances with others.
- The scale of First Nations’ maps often corresponded to travel times rather than absolute distances. As a result, two identical real-world distances would not be identical on the map if one route required more travel time due to rough terrain.
Self-Check 1
- Determine the length of
 in Example 1: Lake Claire. Answer
in Example 1: Lake Claire. Answer
- Complete question 15 on page 110 of the textbook. Answer
1.4. Explore 3
Module 2: Trigonometry
Using the Sine Law to Solve for Angles
The sine law can also be used to solve for angles. When using the sine law, solving for an unknown is easier when the unknown is in the numerator. For this reason, the following equivalent form of the sine law is usually used when solving for angles:

Courtesy NASA/JPL-Caltech
You have looked at mapping land surface with examples from England, Alberta, and early First Nations peoples. The same mathematics is also useful in exploring outer space! In July 2003, NASA launched the Mars exploration rovers Spirit and Opportunity. The rovers’ 90-day missions were designed to investigate the history of water on Mars using a number of onboard science instruments.
At the beginning of each Mars day, each rover receives a set of instructions that tells the rover where to go and what scientific experiments to perform at each location. It is up to the rovers’ hazard avoidance software to determine how to get to each location. Look at Mars Terrain Images to see examples of the types of terrain the rovers must navigate around. The multimedia piece shows real images from Mars—none are artist’s conceptions. In each image, see if part of a Mars rover is visible.
Sending instructions from Earth on where the rovers should go and what experiments should be performed takes time. Round-trip communication time ranges from 6 min (when Mars is closest to Earth) to 44 min (when Mars is farthest from Earth). This time delay is much too long to allow real-time control of the rovers. For this reason, the rovers must determine their own paths for getting to targets.
Example 2: Mars Exploration Rover
The Mars exploration rover Opportunity has been given instructions to go from point A directly east to point B. Due to obstacles in its path, the Rover Hazard Avoidance software has picked a path that has the rover going at an angle of 41° for 5 m toward C and then going 3.5 m to get to B.
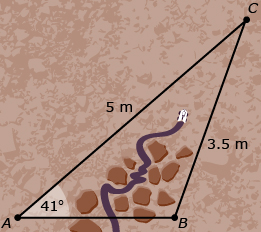
The rover software must determine ∠C so it can determine the correct angle to rotate once the rover reaches point C. The first step is to determine ∠B using the sine law. You will complete the last step, calculating ∠C, after Try This 2.
Step 1: Determine ∠B using the sine law. In other words, write the sine law using a side-angle pair that you know and the side-angle pair with the unknown angle.

Wait a minute! ∠B in the initial diagram is clearly greater than 90°, but a value of 70° was calculated. How can this be? It turns out that the math is correct, but there is something subtle going on. You might like to think back to finding solutions for sin θ = k, where −1 ≤ k ≤ 1.
Try This 2
The given information in Example 2: Mars Exploration Rover was as follows:
- ∠A = 41°
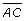 = 5 m
= 5 m
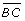 = 3.5 m
= 3.5 m
Use Mars Rover Example to see if another solution is possible—a solution that resembles the oblique triangle shown in the image at the beginning of Example 2: Mars Exploration Rover. The applet allows you to move point B while keeping the measurements provided as given information.
You should have been able to construct two triangles: one with ∠B = 70° and the other with ∠B = 110°. Mars Rover Triangle: Given Information will help you understand why there are two triangles with the measurements specified.
Knowing that the correct value for ∠B is 110° allows you to complete the final step of your calculation.
Step 2: Calculate ∠C using the fact that the sum of angles in any triangle always adds to 180°.
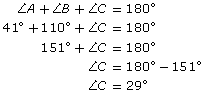
1.5. Explore 4
Module 2: Trigonometry
The Sine Law Ambiguous Case
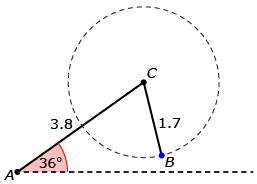
The ambiguous case is the name mathematicians use for scenarios like Example 2: Mars Exploration Rover. The ambiguous case occurs whenever you are trying to solve a triangle problem and the only given information is two sides and an angle opposite one of those sides. Whether or not a triangle falls under the ambiguous case depends on the measures of the sides and angle given.
Try This 3
You will use Ambiguous Case Explorer to investigate the different possibilities in a similar scenario.
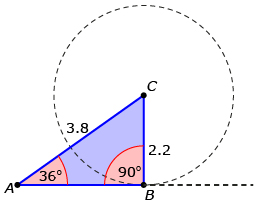
In this scenario the given information is as follows:
- ∠A = 36°
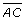 = 3.8
= 3.8
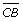 = a value that you specify
= a value that you specify
By changing the length of ![]() using the slider at the bottom, you also change the number of triangles that can be created with the specified sides and angles.
using the slider at the bottom, you also change the number of triangles that can be created with the specified sides and angles.
Answer the following questions using Ambiguous Case Explorer.
- What are the conditions for the length of
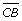 that result in no possible triangles?
that result in no possible triangles?
- What are the conditions for the length of
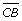 that result in one possible triangle?
that result in one possible triangle?
- What are the conditions for the length of
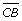 that result in two possible triangles?
that result in two possible triangles?
- Are there values for the length of
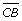 that result in more than two possible triangles?
that result in more than two possible triangles?
- Based on your observations, create a rule that relates the length of
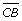 to the number of possible triangles.
to the number of possible triangles.
Share 3
Share your observations in question 5 of Try This 3 with a partner. Try to come to agreement on the rule.
1.6. Explore 5
Module 2: Trigonometry
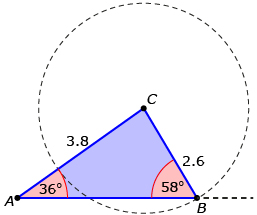
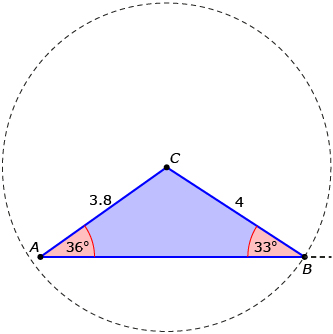
What you may have concluded is that, depending on the length of CB, there may be zero, one, or two possible triangles whose sides and angle match the given values. The following table summarizes your findings.
In this example, a length of 2.2 for CB can be thought of as a dividing line.
If CB is exactly equal to 2.2, then there is only one triangle possible—a right triangle. |
c GeoGebra Creative Commons Attribution-Share Alike 3.0 or later |
| If CB is less than 2.2, there are no possible triangles. |
c GeoGebra Creative Commons Attribution-Share Alike 3.0 or later |
| If CB is greater than 2.2 but less than 3.8, there are two possible triangles. | Triangle 1
c GeoGebra Creative Commons Attribution-Share Alike 3.0 or later
Triangle 2
c GeoGebra Creative Commons Attribution-Share Alike 3.0 or later |
| If CB is greater than 3.8, only one triangle is possible. |
c GeoGebra Creative Commons Attribution-Share Alike 3.0 or later |
This discussion has been in the context of two particular triangles. In order to solve problems in the future, you need to understand how these different cases (zero, one, or two triangles) can result, regardless of what measurements you are given.
The key to understanding this is that the “dividing” point in the above example (a = 2.2) corresponds to a right triangle.
c GeoGebra Creative Commons Attribution-Share Alike 3.0 or later
You used Ambiguous Case Explorer to determine the dividing point of 2.2 (side a above). Since a length of 2.2 corresponds to a right triangle, finding the length of a can be easily calculated:
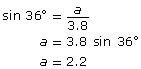
Using standard triangle notation, this can be written as a = b sin A.
Read “The Ambiguous Case,” starting on page 104 of the textbook, for a discussion of how to determine the number of possible triangles for any situation. In this discussion the textbook labels the dividing point as h (because it is the height of a right triangle). Notice that there are two scenarios:
- when ∠A is acute
- when ∠A is obtuse
“Key Ideas” on page 107 of the textbook provides an excellent summary of the sine law and, in particular, the ambiguous case. Read that section and update your copy of Formula Sheet.
Read “Example 3” on page 106 of the textbook for an example of determining measurements of a triangle when the ambiguous case occurs. Ensure that you understand all the steps before moving on to Self-Check 2.
Self-Check 2
Complete questions 6.a., 6.b., 8.a., 8.b., and 11 on pages 108 and 109 of the textbook. Answers
1.7. Connect
Module 2: Trigonometry
Open the Lesson 4 Assignment you saved in your course folder at the start of this lesson. Complete the assignment.
![]() Save all your work in your course folder.
Save all your work in your course folder.
Going Beyond
Read “Proof” on page 102 of your textbook. This is only valid for acute triangles. Write a proof of the sine law for an obtuse triangle, such as the one shown.
Start by extending segment ![]() and drawing a perpendicular segment to vertex C.
and drawing a perpendicular segment to vertex C.
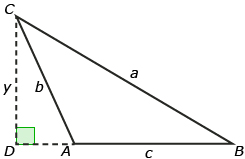
Write the sine ratio for ∠B using ![]() and also for ∠DAC using
and also for ∠DAC using ![]()
1.8. Lesson 4 Summary
Module 2: Trigonometry
Lesson 4 Summary
In Lesson 4 you investigated the following questions:
- How can angles and sides in any triangle—oblique and right—be found?
- How does your knowledge of solutions to equations of the form sin θ = k (from Lessons 1 and 2) affect solutions using the sine law?
You learned and applied a new formula, the sine law, that is valid for all triangles—both right and oblique.
![]()
You also learned that when using the sine law to solve for angles, you must be aware of something called the ambiguous case—depending on the angle and side measurements given in your problem, it may be possible to construct zero, one, or two triangles. Refer to “Key Ideas” on page 107 of the textbook for a summary of the conditions that result in zero, one, or two triangles.
In the next lesson you will learn about the cosine law.