Lesson 5
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-1 SS |
| Book: | Lesson 5 |
| Printed by: | Guest user |
| Date: | Monday, 15 September 2025, 2:28 PM |
Description
Created by IMSreader
1. Lesson 5
Module 2: Trigonometry
Lesson 5: The Cosine Law
Focus
© shiyana/30449451/Fotolia
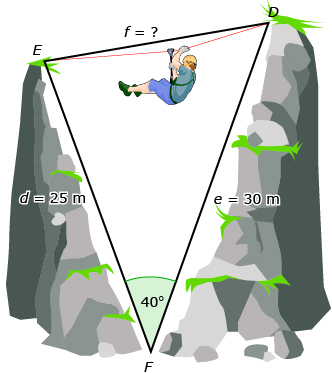
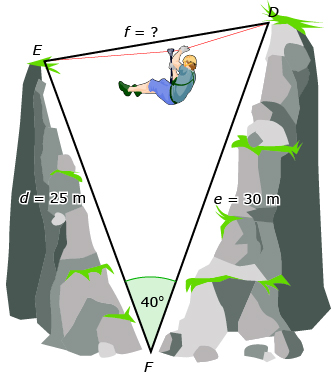
David and Jennifer are designing an obstacle course. They have a number of different tasks that participants need to complete along the course. David and Jennifer need to determine what supplies to purchase in order to construct the course. They are able to directly measure angles and distances for many of the tasks, but some of the angles and distances aren’t easily measured directly.
For the first task, participants will hang onto a rope while crossing a rapidly flowing stream that is about 1 m deep. David and Jennifer need to know the distance across the stream to be sure that the rope is long enough.
They don’t have a tape measure long enough to measure this distance, so they decide to calculate this value by creating a triangle using measurements they can make. If you can create a triangle using values that can be measured, you can often calculate the missing value using trigonometry.
David and Jennifer know the measures of the canyon walls and the angle at the bottom, as shown in the following diagram. The rope corresponds to
You will discover as you work through the lesson how David and Jennifer can determine the value of
Outcomes
At the end of this lesson you will be able to
- use the cosine law to solve for sides or angles in oblique triangles
Lesson Questions
You will investigate the following questions:
- How can angles and sides in any triangle—oblique and right—be found?
- How do you determine when to use the sine law and when to use the cosine law?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 5 Assignment (Download the Lesson 5 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Module 2 Glossary Terms and Formula Sheet
- work under Project Connection
1.1. Discover
Module 2: Trigonometry
Discover
In Lesson 4 you learned that the sine law can be used for any triangle, including oblique and right triangles. Although it is true that the sine law can be applied to any triangle, sometimes you are not given all of the information you need to use the sine law.
Consider Jennifer and David’s problem. They have not been given enough information to conclude that their triangle is a right triangle, so they know that they can’t use the primary trigonometric ratios or the Pythagorean theorem. In math class, they learned that the sine law can be used for any triangle. However, they are not sure that they have enough information to use the sine law.
Share 1
Consider the triangle that David and Jennifer created to help them find the length of the rope they need to purchase.
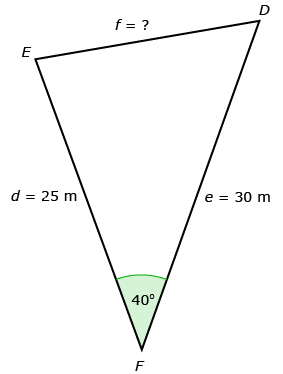
With a partner, write the three equations for the sine law you learned in Lesson 4. Why can’t the sine law be used to find the length of 
If required, save a copy of your discussion in your course folder.
1.2. Explore
Module 2: Trigonometry
Explore
David and Jennifer don’t have enough information to use the sine law. However, there is another formula, the cosine law, which is also valid for any triangle.
The cosine law is usually written in the following way:
a2 = b2 + c2 − 2bc cos A |
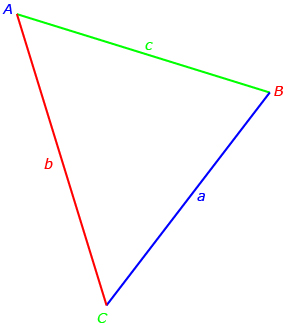
Recall from Lesson 4 that mathematicians typically label sides with lowercase letters and angles with uppercase letters. Furthermore, sides and angles with the same letter are across from one another. For instance, side a is across from ∠A.
Keep this naming convention in mind. The variable, A, in the equation must be the measure of the angle across from side a, which is the measure you’ll be trying to determine. Look closely at the equation a2 = b2 + c2 − 2bc cos A. In order to determine the length of side a in the equation, you must know the
- lengths of the other two sides (b and c)
- angle across from the side you are trying to determine (A)
Try This 1
c GeoGebra Creative Commons Attribution-Share Alike 3.0 or later
Use Cosine Law Explorer to see if the cosine law is valid for any triangle. Drag the vertices of the triangle, and confirm that the left side of the cosine law is always equal to the right side. Can you create a triangle where the cosine law will not work?
Save your response in your course folder.
1.3. Explore 2
Module 2: Trigonometry
Understanding the Relationships in the Cosine Law
Cosine Law Illustrator may help you better understand the relationships among a, b, c, and ∠A in the cosine law.
Read “Link the Ideas: The Cosine Law” on page 116 of the textbook. This section includes a proof of the cosine law for acute triangles. In the Going Beyond section of this lesson you will complete a proof of the cosine law for obtuse triangles.
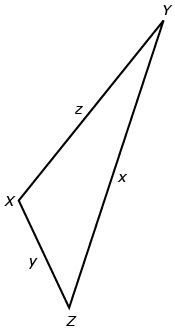
Self-Check 1
Given the following triangle, state three different ways the cosine law can be written, depending on which angle you are working with. Answer
Example 1: The Obstacle Course
The cosine law can be used to solve the problem given in the Focus section.
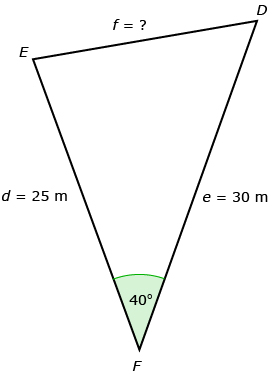
Start by stating the correct cosine law for the question.
f 2 = d2 + e2 − 2de cos F
Remember that the angle in the equation is the angle across from the side you are trying to determine. In this example, ∠F is across from the side you are trying to determine.
f 2 = 252 + 302 − 2(25)(30) cos 40°
You might enter the equation above in more than one step. Remember that most calculators can deal with complicated expressions. Just enter the equation above, exactly as you see it. You will get this answer:
f 2 = 375.9333…
You must use the unrounded answer from your previous step. Many calculators let you do this using the ANS key, which stands for “answer from previous step.” For some calculators, you would enter 
Consult your calculator manual if you can’t find the ANS key on your calculator.
The unrounded value for f is 19.3890…. Round the final answer to one decimal place unless instructed otherwise.
f = 19.4 m
Read “Example 1: Determine a Distance” on page 116 of your textbook. Ensure that you are comfortable with the steps in this solution before moving on.
Self-Check 2
Complete questions 1.a., 1.c., 5.b., and 6.a. on pages 119 and 120 of the textbook. Answers
1.4. Explore 3
Module 2: Trigonometry
Using the Cosine Law to Solve for Angle Measures
The cosine law can also be used to determine angle measures. Because the formula includes one angle, if you are given all three sides, you can use the cosine law to solve for any angle in a triangle.
Read “Example 2: Determine an Angle” on page 117 of the textbook. Notice the two methods for using the formula.
- In Method 1, values are substituted directly into the formula.
- In Method 2, the formula is rearranged before the values are substituted.
Many students prefer Method 2—substituting values after the formula has been rearranged. As shown in your textbook, the rearranged form is
Self-Check 3
Given the following triangle, state three different ways the cosine law can be written when all three sides are given and you are solving for unknown angles. Answer
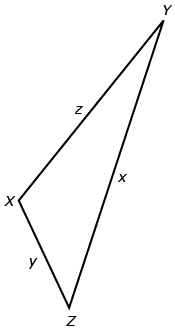
Try This 2
Rahim is learning how to use a compass in an orienteering course. He is standing at checkpoint C and knows distances to two other checkpoints, as shown in the diagram. In order to walk in the correct direction, Rahim needs to determine the angle between checkpoints A and B (∠θ on the diagram).
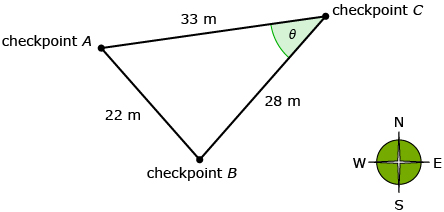
Rahim used the cosine law to determine ∠θ. Each step he used is described below. Write the mathematical formula or calculation described in each of the steps. Use the hints if you are stuck or if you need to check your progress.
Step 1: Write a correct version of the cosine formula. 
Step 2: For this problem, ∠θ is across from the side that is 22 m long. Rahim replaces C in the formula with θ because that’s how the angle is labelled in his diagram. Then Rahim substitutes all the variables for values from the triangle.
Step 3: Rahim calculates what cos θ is equal to using his calculator.
When entering fractions on a calculator, extra care must be taken with brackets. The easiest approach is to always put the numerator in brackets and the denominator in brackets.
For this example, you would enter the following in your calculator:
(332 + 282 − 222)/(2(33)(28))
Step 4: Rahim uses his calculator to find θ.
Step 5: Rahim remembered to round his answer to the nearest degree.
Save your responses in your course folder.
Self-Check 4
After you answer the questions, make sure you check the suggested answers carefully to ensure you understand the solution process. If you are still having trouble, contact your teacher.
Complete questions 2.a., 2.c., 5.c., and 17 on pages 119 to 122 of the textbook. Answers
Add both forms of the cosine law to your copy of Formula Sheet.
1.5. Connect
Module 2: Trigonometry
Open the Lesson 5 Assignment you saved in your course folder at the start of this lesson. Complete the assignment.
Save all your work in your course folder.
Project Connection
images: Courtesy NASA/JPL-Caltech
You are now ready to complete the remaining questions, 7 to 11, of Module 2 Project: Mars Rover Simulation.
Save all your work in your course folder.
Going Beyond
The proof in “Link the Ideas: The Cosine Law” on page 116 of the textbook is only valid for acute triangles. Here is a partial proof for the cosine law for obtuse triangles.
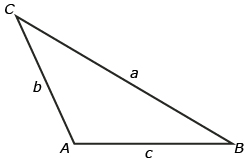
The first step is to extend AB and draw a perpendicular segment to vertex C.
Two expressions can be written using 
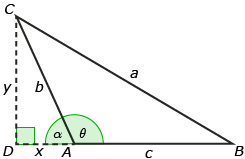
equation 1: 
equation 2: b2 = x2 + y2
The Pythagorean theorem can be used again in 
equation 3: a2 = y2 + (x + c)2
Equation 2 can be rearranged to obtain y2 = b2 − x2. Substituting this rearrangement into equation 3 and then simplifying results in the following equation:
equation 4: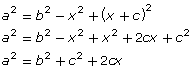 
Equation 1 can be rearranged to obtain x = b cos α. Substituting this rearrangement into equation 4 results in the following equation:
a2 = b2 + c2+ 2bc cos α
This is close to the cosine law. If you can show that cos α = −cos θ, then the cosine law results:
Your task in this Going Beyond is to explain why cos α = − cos θ.
Save your response in your course folder.
1.6. Lesson 5 Summary
Module 2: Trigonometry
Lesson 5 Summary
In this lesson you learned that although the sine law is valid for all triangles, sometimes you are not given enough information to use the sine law.
You also learned the cosine law, which is valid for all triangles (just like the sine law):
a2 = b2 + c2 − 2bc cos A or 
When deciding whether to use the sine law or the cosine law, consider which values are given and which values you need to find.
- If you have a side-angle pair (i.e., one side and its opposite angle), then you can use the sine law.
- If you do not have a side-angle pair, then you will likely need to use the cosine law.
If you think back to the obstacle course in the Focus section, David and Jennifer did not have a side-angle pair. Therefore, the cosine law was used to find the length of rope needed.
Khan Academy (CC BY-NC-SA 3.0)
For a summary review of how to come up with the cosine law, watch “Law of Cosines” from the Khan Academy.