Lesson 2
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-1 SS |
| Book: | Lesson 2 |
| Printed by: | Guest user |
| Date: | Thursday, 4 December 2025, 2:15 AM |
Description
Created by IMSreader
1. Lesson 2
Module 4: Quadratic Equations and Inequalities
Lesson 2: Solving Quadratic Equations by Factoring
Focus

iStockphoto/Thinkstock
Have you ever taken something apart because you wondered how it worked? Maybe your motivation was not to uncover the design of the object but to repair the object instead. Whether you are modifying, repairing, or just satisfying your curiosity, reducing something to its parts is a common strategy for problem solving.
This strategy lets you focus your attention on smaller parts of the problem or object. By figuring out the problem one piece at a time, you can figure out the whole problem.
In this lesson you will use the reduction strategy to solve quadratic equations. You will use factoring to break a quadratic equation into its parts.
Outcomes
At the end of this lesson you will be able to
- factor a given polynomial expression that requires the identification of common factors
- factor a given polynomial expression of the form ax2 + bx + c, a ≠ 0, and a2x2 − b2y2, a ≠ 0
- factor a given polynomial expression that has a quadratic pattern
- solve a quadratic equation of the form ax2 + bx + c = 0 by factoring
Lesson Questions
You will investigate the following questions:
- How can previous patterns of factoring be extended to polynomial expressions?
- How does the zero-product property relate to solving quadratic equations by factoring?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 2 Assignment (Download the Lesson 2 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Module 4 Glossary Terms and Formula Sheet
- work under Project Connection
1.1. Launch
Module 4: Quadratic Equations and Inequalities
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? This section, which includes Are You Ready? and Refresher, will help you find out.
Before beginning this lesson you should be able to
- factor polynomials
- factor difference of squares
- factor trinomials
1.2. Are You Ready?
Module 4: Quadratic Equations and Inequalities
Are You Ready?
Complete these questions. If you experience difficulty and need help, visit Refresher or contact your teacher.
- What does it mean to factor? Answer
- Factor the following polynomials.
-
Factor the following differences of squares.
-
Factor the following trinomials.
-
Factor the following trinomials.
How did the questions go? If you feel comfortable with the concepts covered in the questions, skip forward to Discover. If you experienced difficulties, use the resources in Refresher to review these important concepts before continuing through the lesson.
1.3. Refresher
Module 4: Quadratic Equations and Inequalities
Refresher
To understand the concepts presented in this lesson, you need to understand factoring binomials and trinomials. Carefully review factoring using the following Refresher resources.
Go to Factor and focus on the first definition that is given.
Review factoring polynomials, factoring difference of squares, and factoring trinomials. Factoring Strategies Chart summarizes some factoring strategies you may have learned in previous math courses. The chart includes examples and provides information and tips about when and how best to use each strategy. You can print this chart for your use as you complete Lesson 2.
Factoring Flowchart can help you make decisions, based on the properties of the polynomial, about when to use each of the factoring strategies. You may have created and saved something similar in a previous math course. If so, feel free to use the flowchart you created. If not, you can print and use Factoring Flowchart.
In Factoring Special Products you will choose the correct steps to factor a polynomial. Feedback is given if you choose incorrect steps.
Review three lessons about factoring from Mathematics 10C Learn EveryWare:
- Lesson 3: Common Factors
- Lesson 4: Factoring Trinomials of the Form ax2 + bx + c
- Lesson 5: Factoring Special
Both pictures: Larrie Thomson/www.nightphotographer.com
Go back to the Are You Ready? questions and try them again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 4: Quadratic Equations and Inequalities
Discover

Try This 1
- Read the Apple Pi cartoon shown. On a scale of 1 to 10, rate how impressed you are that the girl guessed the correct integers?
- One of the numbers is easy to guess from the clue that is given. Which number is it and why should it be easy to guess that number?
- Consider the three quadratic equations in the chart. For each equation, determine the roots from the graph then factor the equation. You can use the chart to summarize your work.
Quadratic Equation Graph Roots Factored Form a. x2 + 3x − 4 = 0 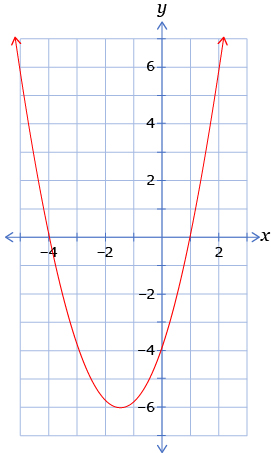
b. x2 − 4 = 0 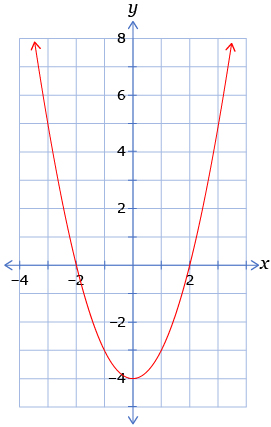
c. 2x2 − 5x + 2 = 0 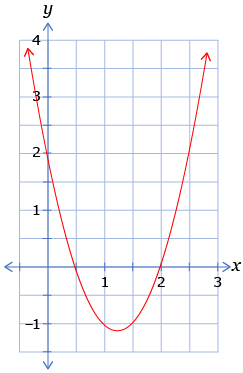
-
How are the roots of a quadratic equation related to the factored form of the equation?
- Suppose the roots of a quadratic equation are 8 and –5. Given these roots, what are the possible factors and a possible quadratic that satisfies the roots?
![]() Save your responses in your course folder.
Save your responses in your course folder.
You will need to retrieve your work later in the lesson.
Share 1
With a partner or in a group, discuss your responses to Try This 1 questions 3 and 4. Summarize your discussion by answering the following question: How is the clue given in the cartoon related to finding the roots of a quadratic equation by factoring?
![]() If required, save your response in your course folder.
If required, save your response in your course folder.
1.5. Explore
Module 4: Quadratic Equations and Inequalities
Explore
Reverse engineering is the process by which an object is taken apart and examined for the purpose of understanding its design and how it is made. Roll over each image in Reverse Engineering Rollover to learn more about each step in the reverse engineering of a car.
In this lesson you will use reverse engineering to unpack a quadratic equation by factoring. You will break quadratic functions into smaller parts by expressing the functions as a product of factors.
1.6. Explore 2
Module 4: Quadratic Equations and Inequalities
In Launch you practised your factoring skills. The patterns you used to factor differences of squares and trinomials in previous math courses can be applied to polynomial expressions that have a quadratic form. Can you see the quadratic form in this polynomial?
4(x + 2)2 − 9(x − 1)2
This polynomial is actually a difference of squares.
Try This 2 will help you factor polynomials with a quadratic form by applying the factoring methods reviewed in Launch.
Try This 2
The table shows two columns. The left column shows a trinomial, or difference of squares, that should look familiar to you. The right column shows a corresponding polynomial in the same quadratic form.
| Examples of Quadratic Expressions |
Examples of Polynomial Expressions with a Quadratic Form |
| 4x2 − 9y2 | 4(x + 2)2 − 9(x − 1)2 |
| x2 − 3x + 2 | (a2)2 − 3(a2) + 2 |
| 3x2 + 8x − 3 | 3(x − 1)2 + 8(x − 1) − 3 |
- Factor each quadratic expression in the column on the left using an appropriate factoring strategy.
- Adapt the same strategy to factor the corresponding polynomial expression in the column on the right. Leave your answer in factored form.

Compare your responses to Try This 2 to similar problems in the textbook. Work through “Example 2” on page 222. Did you use one of the two methods shown?
To check your strategy, confirm your final factored form.
4(x + 2)2 − 9(x − 1)2 = (5x + 1)(−x + 7)
(a2)2 − 3(a2) + 2 = (a2 − 2)(a + 1)(a − 1)
3(x − 1)2 + 8(x − 1) − 3 = (3x − 4)(x + 2)
1.7. Explore 3
Module 4: Quadratic Equations and Inequalities
Equations of the Quadratic Type
Can you see the quadratic form in this polynomial: 4(x + 2)2 − 9(x − 1)2?
What if you let t = (x + 2) and r = (x − 1)? Now can you see the quadratic form 4t2 − 9r2?
As you saw in part a of “Example 2” in the textbook, you can use a method of replacing a binomial with a single variable to temporarily “declutter” the quadratic. You can then factor the quadratic using a method your are familiar with. When the math is done, the expressions t = (x + 2) and r = (x − 1) are placed back into your final expression.
It is important to include the brackets around the binomials when placing the binomials back into your expression because, in some cases, a sign may change.
In Try This 2 you may have used a factoring strategy similar to the one used in “Example 2,” part b. This strategy applies the difference-of-squares factoring pattern P2 − Q2 = (P − Q)(P + Q) to any polynomial in quadratic form.
It does not matter which method you choose; the final factored form will be the same.
Self-Check 1
1.8. Explore 4
Module 4: Quadratic Equations and Inequalities
Zero-Product Property
In the cartoon in Discover, the girl was able to guess that one of the two integers was zero based on the clue that the product of the two integers was zero. This is an example of the zero-product property.
If the product of two or more numbers is zero, the value of at least one of those factors is zero. For example, if a × b = 0, one of the following must be true:
- a = 0
- b = 0
- both a = 0 and b = 0
The zero-product property is a key idea in solving quadratic equations by factoring. Watch Zero-Product Property in Action to see why. Before you begin watching, retrieve your work from Try This 1. Compare the process you used with what you see in the video.
In the last lesson you learned that the solution of a quadratic equation could contain one root, two roots, or no roots. In the next part of the lesson you will investigate the relationship between the factored form of a quadratic equation and the number of roots in the solution.
Turn to “Example 3” on pages 223 to 225 in the textbook. Work through the example, paying attention to the following:
- the reasoning for each step
- the different factoring methods presented
- the number of distinct roots in each solution
Complete Try This 3 based on what you have read. You will find some of the same equations that you encountered in the textbook. Keep your textbook handy in case you need to refer to those pages.
Try This 3
For each of the quadratic equations in the first column, graph the corresponding quadratic function and indicate the number of distinct roots. Then express the quadratic equation in factored form.
Note: You may encounter quadratic equations that cannot be factored normally. In those cases, you can write “Not factorable.”
| Quadratic Equation | Solution by Graphing | Number of Distinct Roots | Solution by Factoring |
| x2 + 6x + 9 = 0 | |||
| 2x2 − 9x − 5 = 0 | |||
| 2x2 + 4 = 0 | |||
| 2x2 + 2x + 1 = 0 |
Share 2
With a classmate, share and compare your charts from Try This 3, and then discuss the following questions.
- How can you tell from the factored form of a quadratic equation whether the equation has one, two, or no roots?
- When will a quadratic equation not have roots? Explain this situation in terms of the graph of the function and the ability to factor the equation.
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.9. Explore 5
Module 4: Quadratic Equations and Inequalities
Solving Quadratic Equations by Factoring
Use Solving by Factoring for guided instruction in solving quadratic equations by factoring. Pay attention to the sequence of steps for this strategy. Don’t be afraid to make a mistake—the applet will give you feedback and a chance to correct your errors.
To get started, do the following:
- Click on Solving Quadratic Equations: Factoring.
- Select the puzzle-piece icon at the top.
- Select Solving by Factoring.
- Choose to do additional examples by pressing the “+” button at the bottom of the window.
Self-Check 2
Check your understanding by completing Do You Know Your Roots?
Try This 4
Now that you have an understanding of how factoring and the zero-product property can help you solve quadratic equations, you are ready to apply the strategies you have learned to real-life contexts.
A uniform tile border is to be constructed around the perimeter of a rectangular swimming pool. The total dimensions of the pool and border are to be 30 m by 15 m. If the pool itself has an area of 324 m2, what is the width of the border?
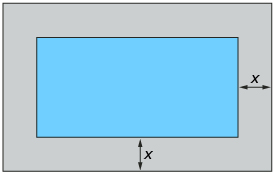
- Copy the diagram of the swimming pool above. What does x represent?
- Complete your diagram by labelling the diagram’s properties with appropriate numbers from the problem description.
- Determine an expression for the length and width of the pool surface.
- Construct a quadratic equation that can be used to determine the width of the border.
![]() Save your work in your course folder.
Save your work in your course folder.
1.10. Explore 6
Module 4: Quadratic Equations and Inequalities
Surprise! You get to check your work from Try This 4 in Swimming Pool Border Solution. Pay attention to how the quadratic equation is set up. Also pay careful attention to the way in which the quadratic equation is factored.
Self-Check 3
Complete questions 11, 12, 17, and 20 on pages 230 to 232 in the textbook. Answers
1.11. Connect
Module 4: Quadratic Equations and Inequalities
Open your copy of Lesson 2 Assignment, which you saved in your course folder at the beginning of this lesson. Complete the assignment.
Project Connection
In Module 4 Project: Imagineering, continue working on Blue Sky. You will complete Blue Sky in Lesson 3.
Going Beyond

There are many methods of factoring a quadratic equation. You may have used algebra tiles to factor polynomials in your previous math studies. That method is also valid for quadratic equations.
An interesting method of factoring a quadratic equation was developed by François Viète, a 16th-century French mathematician. You may remember Monsieur Viète, from Mathematics 10C Learn EveryWare, as the code-cracking King’s advisor who used his math skills to decipher enemy correspondence in France’s war with Spain. The factoring algorithm he used is based on substitution.
Watch Factoring by Substitution to see the steps of the algorithm. Then try applying the steps to any of the quadratic equations you have encountered in this lesson.
1.12. Lesson 2 Summary
Module 4: Quadratic Equations and Inequalities
Lesson 2 Summary

In this lesson you investigated the following questions:
- How can previous patterns of factoring be extended to polynomial expressions?
- How does the zero-product property relate to solving quadratic equations by factoring?
In the real world you may take apart an object or reduce the object to its component parts in order to troubleshoot problems. An engine can be rebuilt in this way. The beautiful sound of a piano may be restored after a professional piano tuner has taken the piano apart to repair the out-of-tune parts. A clogged sink drain may need to be taken apart in order to clear the clogged portion.
In mathematics, factoring is a way in which polynomials can be reduced to parts. In this lesson you reviewed factoring strategies that you learned in a previous math course. You extended those patterns to the factoring of polynomial expressions by looking for common structures between quadratic and polynomial expressions.
You investigated the zero-product property, which states that if the product of two or more factors is equal to zero, at least one of the factors is equal to zero. The method of solving quadratic equations by factoring the equations and then setting each factor to zero is based on the zero-product property.
You applied the zero-product property to the solution of quadratic equations. By setting a quadratic equation to zero and factoring the quadratic expression, you expressed the equation as a product of factors. Since the equation is equal to zero when either or both of the factors are equal to zero, the roots can be determined by setting each factor to zero.
In the next lesson you will learn another algebraic method for solving quadratic equations. This method will eventually lead to a formula that you can use to solve any quadratic equation algebraically!