Lesson 3
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-1 SS |
| Book: | Lesson 3 |
| Printed by: | Guest user |
| Date: | Monday, 15 September 2025, 2:28 PM |
Description
Created by IMSreader
1. Lesson 3
Module 4: Quadratic Equations and Inequalities
Lesson 3: Solving Quadratic Equations by Completing the Square
Focus
Hemera/Thinkstock
iStockphoto/Thinkstock
© Chee-Onn Leong/2054383/Fotolia
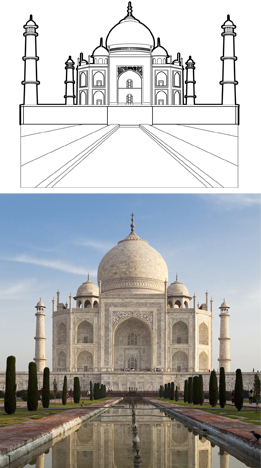
Have you ever seen a beautiful building? You may have travelled to places and seen immense structures with strange but appealing designs. You may have some beautiful buildings in your own community. Consider the photos shown. What is the difference between each sketch and its accompanying photo? Does the absence of landscape features in the sketches add to, or subtract from, the beauty of the buildings?
Landscaping is an important part of beautifying an area, especially the grounds of important buildings such as the Taj Mahal in Agra, India. Landscape design and landscape architecture are both professions that deal with the design and development of public spaces to meet minimum standards of beauty, practicality, and environmental impact.
In this lesson you will learn how to solve quadratic equations by completing the square. You will investigate problems related to landscape design that can be modelled and solved using quadratic equations.
Outcomes
At the end of this lesson, you will be able to
- solve a quadratic equation of the form ax2 + bx + c = 0 by determining square roots
- solve a quadratic equation of the form ax2 + bx + c = 0 by completing the square
Lesson Questions
You will investigate the following questions:
- In what circumstances would completing the square be favourable over other strategies for solving quadratic equations?
- What is the goal of completing the square, and how does this help determine the roots of a quadratic equation?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 3 Assignment (Download the Lesson 3 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Module 4 Glossary Terms and Formula Sheet
- work under Project Connection
1.1. Launch
Module 4: Quadratic Equations and Inequalities
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? This section, which includes Are You Ready? and Refresher, will help you find out.
Before beginning this lesson, you should be able to
- identify perfect square trinomials
- factor perfect square trinomials
- write radicals in simplest form
- convert quadratic functions into vertex form by completing the square
1.2. Are You Ready?
Module 4: Quadratic Equations and Inequalities
Are You Ready?
Complete these questions. If you experience difficulty and need help, visit Refresher or contact your teacher.
- What is a perfect square trinomial? How do you know if a trinomial is a perfect square trinomial? Answer
- Factor each perfect square trinomial.
- Convert the following quadratic functions into vertex form by completing the square.
- Write each radical in simplest form.
How did the questions go? If you feel comfortable with the concepts covered in the questions, skip forward to Discover. If you experienced difficulties, use the resources in Refresher to review these important concepts before continuing through the lesson.
1.3. Refresher
Module 4: Quadratic Equations and Inequalities
Refresher
Use the following to review the topics you experienced difficulties with in the Are You Ready? section.
Search the Internet for a definition of perfect square trinomials. One way to obtain the definition for any word is to use a search engine. When there are several words in an expression, use quotation marks. For example, you can enter “perfect square trinomial” to find this definition.
Go to Module 3: Lesson 5, page 3 in Mathematics 10C Learn EveryWare. Near the bottom of this page is the section “Factoring Perfect Square Trinomials.” You can find the definition in this section as well as an example showing how you can identify and factor a perfect square trinomial.
Go to Module 4: Lesson 4, page 4 in Mathematics 10C Learn EveryWare. Review “Example 1” and “Example 2” to see several methods of converting entire radicals to simplified mixed radicals.
Practise converting quadratic functions into vertex form by completing the square in Completing the Square.
Go back to the Are You Ready? section and try the questions again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 4: Quadratic Equations and Inequalities
Discover
Each of the rectangles in the image has something in common with the other rectangles. Can you guess what that is?
In this Math Lab activity you will confirm your hypothesis and discover an interesting aspect of design.
Problem
For a rectangle with constant perimeter, what dimensions of the rectangle will give you the maximum area?
Consider the problem; then write down a hypothesis.
Procedure
Use Rectangle Drawer to construct rectangles of different shapes.
Analysis
- What dimensions of a rectangle give you the maximum area?
- Assume that a rectangle has an area of 306 cm2. The perimeter of the rectangle is 70 cm. Determine the dimensions of the rectangle by
- using Rectangle Drawer
- solving a quadratic equation
- using Rectangle Drawer
Save your work in your course folder.
Keep your answers to this Math Lab handy. You will revisit the ideas developed here later in the lesson.
1.5. Explore
Module 4: Quadratic Equations and Inequalities
Explore
Digital Vision/Thinkstock
Landscape engineering, or just landscaping, is the discipline where science and mathematics are used to shape landscapes. A landscape engineer plans and designs the landscape to meet certain criteria, such as minimizing costs or maximizing green space. Those who hire landscape engineers may also have a specific look in mind. Therefore, the aesthetics of the project are also important. Like other engineers, landscape engineers apply mathematical principles to build landscapes and to overcome anticipated design problems.
In this lesson you will extend the concept of completing the square to solving quadratic equations. You will build the foundational skills and understanding that will be important in the next lesson when you develop a formula for solving any quadratic equation.
You have learned several ways of solving quadratic equations. You can select an appropriate strategy for solving a quadratic equation based on how the equation is presented. Try the next activity to see if you can find an efficient way of determining the roots of some quadratic equations.
Try This 1
- Consider the quadratic equation (x − 1)2 = 9. There are different ways of solving this equation. Show how you would solve this equation algebraically. How many roots are there?
- Consider the equation x2 = 9. How is this equation similar to the equation (x − 1)2 = 9?
- Solve the equation x2 = 9 using the same strategy you used to solve (x − 1)2 = 9. How many roots are there?
- Describe other ways to solve these equations.
Save your work in your course folder.
Share 1
With a classmate, compare your solving strategies and solutions for Try This 1. The solutions to the equations should be the same, regardless of the method used.
- If your solutions differ, work together to determine where the algebraic error was made.
- If your solutions are the same but you used different strategies, try solving the equations using your classmate’s method.
- If you used the same method and arrived at the same solution, try solving the equations using a completely different method. See if you can reach the same answer you were able to obtain with your original solving strategy.
Did either of you use the following strategies?
- Expand and then factor a trinomial.
- Rearrange the terms and then factor a difference of squares.
- Take the square root of each side.
If not, give one or two of these strategies a try.
Save any changes you made to the Try This 1 questions in your course folder.
Keep your file open for the next part of the lesson.
1.6. Explore 2
Module 4: Quadratic Equations and Inequalities
Using Square Roots to Solve Quadratic Equations
Recall that the square of any number other than zero is positive. There are always two equal and opposite roots when you take the square root of an equation in the form x2 = a, where a is a real number other than zero.
x2 = a
When x ≠ 0, a > 0.
Applying the square root to both sides of the equation results in
Two equal and opposite sides!
You may have used one of the following strategies to solve the question in Try This 1. Watch Using Square Roots to Solve Quadratic Equations. You will see two ways to solve quadratic equations by taking the square root of the expressions on each side of the equation.
From the video, you can see that when a quadratic equation is in the form (x − p)2 = a, you can use the square roots strategy to determine the equation’s roots. In the previous module you learned that a quadratic function in standard form, y = ax2 + bx + c, can be expressed in vertex form, y = a(x − p)2 + q, by completing the square. You can extend the principle of completing the square to quadratic equations.
Try This 2
- Each quadratic function on the left has been converted to the form y = a(x − p)2 + q by completing the square. Use a similar method to convert the corresponding quadratic equation to the form 0 = (x − p)2 + q.
Quadratic Function
Quadratic Equation
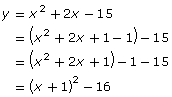
x2 + 2x − 15 = 0
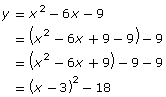
x2 − 6x − 9 = 0
- Working with the completed square (or vertex) form of each quadratic equation in question 1, rearrange the equations into the form (x − p)2 = q.
- Use the square root strategy shown in the video to determine the roots of each quadratic equation.
- Check your answers. Remember that you have learned multiple methods of solving quadratic equations, both algebraic and graphical ones.
Save your solutions in your course folder.
It’s important that you get this one right before moving on. Check your rearrangement:
|
|
1.7. Explore 3
Module 4: Quadratic Equations and Inequalities
When you have an equation of the form (x − p)2 = q, it may be tempting to square the binomial and then collect like terms. For example:
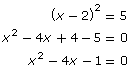
This method, however, overlooks the advantage of having the vertex form of the equation. Instead, by taking the square root of both sides of the equation, you will be within steps of determining the roots.
Turn to “Example 2” on page 237 of the textbook to see how you can solve a quadratic equation by completing the square. As you work through the solution, look for the answers to the following questions:
- To what form is the quadratic equation reduced in the very first step?
- Why is 25 added to each side?
- How are you supposed to solve
?
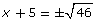Self-Check 1
Work through Completing the Square.
You have now learned how to solve quadratic equations of the form x2 + bx + c = 0 by following the steps in the table.
| Step | Description | Example for the General Case |
| 1 | Complete the square. | x2 + bx + c = 0 |
| 2 | Work with the squared expression. |  |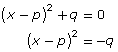
| 3 | Square root both sides of the equation. |  |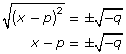
| 4 | Isolate the root. |  |
Notice that in the examples, a = 1. Now consider how you might apply the same process to solve quadratic equations in the general form ax2 + bx + c = 0, where a ≠ 1.
In Try This 3, you will again convert the general form into the form a(x – p)2 + q = 0 by completing the square. Pay special attention to what happens to a now that a ≠ 1.
There are two cases to consider when you subtract 5 from the other side of the equation:
1.8. Explore 4
Module 4: Quadratic Equations and Inequalities
Try This 3
Consider the quadratic equation 3x2 – 18x + 7 = 0. (Notice that a = 3.) Complete the steps in Try This 3 Table to determine the roots as exact values. You can print a copy of this table if you prefer.
Save your work in your course folder.
Keep your copy of Try This 3 Table open for the following Share activity.
Share 2
Compare your results with a classmate. Discuss the reasoning for each step. You may want to add a third column, titled “Reasoning,” to your copy of Try This 3 Table. Record the main points of your discussion.
Try solving a similar quadratic equation together.
Save a copy of your discussion in your course folder.
Turn to “Example 3” on page 238 of the textbook to see a slightly different way of solving a quadratic equation of the form ax2 + bx + c = 0, where a ≠ 1. Work through the example to see how this alternate way of completing the square is accomplished. As you do, ask yourself the following questions:
- How does the first step in the solution address the issue of a negative value for a? How does this simplify the solution process? How does this step make the solution process more challenging?
- How do you enter the exact value in your calculator? Be sure that you use your own calculator to check that you can obtain the same roots as shown in the example.
Self-Check 2
Complete Finding the Roots!
You would have to enter the exact values separately as follows:
1.9. Explore 5
Module 4: Quadratic Equations and Inequalities
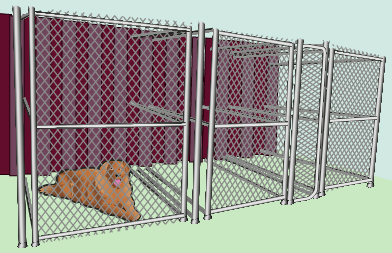
A dog run is a fenced off area, usually in a yard, where a dog can be confined. A dog run keeps the family pet out of the nicely landscaped yard while still providing ample space for the dog to exercise.
As you already know from the previous lessons, you can model various problems with quadratic equations. You can solve these equations by completing the square. Complete Try This 4 to solve a design problem involving a dog run.
Try This 4
Carmen wants to create a dog run for her three dogs. She plans to fence three distinct areas as shown—one for each dog. In order to save on the cost of chain link fencing, she plans to place the dog run on a concrete pad and position it so that the yard fence can be used as the fourth side. Carmen has 20 m of fencing available. She would like to build a dog run with the greatest area between the house and garage.
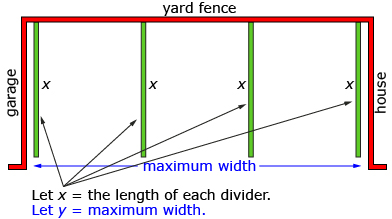
- Determine the maximum area of the dog run. What will the dimensions be for each compartment?
If you get stuck, access one of these hints:
- How do I set up the equations?
- What do I do with the equations?
- How do I determine the length?
- How do I determine the width?
- How will I know if I found the correct dimensions?
- How do I set up the equations?
- Suppose the distance between the garage and the house is 9 m. Will Carmen be able to construct a dog run with the maximum area from the previous question? Support your reasoning.
Stuck? Try this hint:
- How do I approach this problem?
- How do I approach this problem?
- Suppose the dog run has an area of 23 m2. For each possible design that satisfies this criteria, determine the dimensions of each compartment.
Hints are available if you need help:
- What equation models this problem?
- How do I solve the equation?
- How many designs should there be?
- How will I know if I got the correct answer?
- What equation models this problem?
Self-Check 3
Complete questions 8, 10, and 11 on pages 241 and 242 of the textbook. Answer
The sum of the areas of each compartment equals the
total area, 23 m2.
The sum of the areas of the three compartments equals the maximum area.
1.10. Connect
Module 4: Quadratic Equations and Inequalities
Open your copy of the Lesson 3 Assignment, which you saved in your course folder at the start of this lesson. Complete the assignment.
Save your work in your course folder.
Project Connection
© wong yu liang/29976438/Fotolia
Complete Step 1: Blue Sky of Module 4 Project: Imagineering.
Save your work in your course folder.
Going Beyond
gazibo: © MRM4/30597136/Fotolia; garden paths: © gallas/23657641/Fotolia; grass field: © Trombax/4094580/Fotolia
Landscape design is where mathematics meets art. You can find examples of outstanding landscape designs as you look at your neighbours’ yards or the grounds of important buildings. There are, however, other feats of landscape design that cannot escape notice. Hedge mazes are examples of how you can create extraordinary works of architecture with otherwise ordinary plants.
Download a copy of the Dole Plantation Maze. See how long it takes you to navigate to each of the coloured points on the maze. How long do you think it would take you to navigate the maze in reality? What advantage do you have in approaching the maze with a paper and pencil as compared to actually walking through the maze?
Use an Internet search engine to view other examples of hedge mazes. In addition to web and image searches, you can also perform video searches. Some people have recorded their journeys through mazes. By watching one of these videos, you can experience the thrill of walking through a maze.
If you have time, you may want to experience a hedge maze near your very own community. In Alberta, there are corn mazes at Bon Accord, Edmonton, Lacombe, Lethbridge, and Rockyview, to name a few. These mazes can be particularly fun at Halloween. In many cases, the mazes are decorated with scary artifacts or actors are hired to jump out when it’s least expected!
1.11. Lesson 3 Summary
Module 4: Quadratic Equations and Inequalities
Lesson 3 Summary
first hedge: © psnoonan/23693382/Fotolia; second hedge: © brozova/24543439/Fotolia
In this lesson you investigated the following questions:
- In what circumstances would completing the square be favourable over other strategies for solving quadratic equations?
- What is the goal of completing the square and how does this help determine the roots of a quadratic equation?
You learned how to determine the roots of a quadratic equation by completing the square. You discovered that, just as you did with quadratic functions, you can convert a quadratic equation in standard form to the form a(x − p)2 + q = 0 by completing the square. This form is used to solve the equation for its roots. The key is to isolate the binomial square and then to take the square roots of each side of the equation. This quickly leads to the isolation of x and the determination of the roots as either exact or approximate values.
Solving a quadratic equation by completing the square has several advantages over the other methods:
- Since the method is an algebraic method, completing the square can show the mathematical principles underlying the solution.
- This method can provide an exact value, whereas graphing methods may not.
- This method helps you solve equations that are not easily factored.