Lesson 4
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-1 SS |
| Book: | Lesson 4 |
| Printed by: | Guest user |
| Date: | Thursday, 4 December 2025, 2:08 AM |
Description
Created by IMSreader
1. Lesson 4
Module 4: Quadratic Equations and Inequalities
Lesson 4: The Quadratic Formula
Focus

phone: Hemera/Thinkstock; water gun: © waleerat wasinsakul/13428332/Fotolia
In the design industry, after a new product has been envisioned, a prototype is often built to test the concept. Once the design is established, it is easy to create variety in the product. In the case of a car, a manufacturer may produce five different colours, offer an automatic or standard transmission, and provide the choice of a standard or deluxe interior. Regardless of which combination of features is selected by the customer, the manufacturer can roll out the desired vehicle because the design has been standardized.
In this lesson you will use a formula to solve quadratic equations. Like the designer of a prototype, you will derive the formula by working with a “prototype,” or a specific example. You will discover that you can apply the formula or design to any quadratic equation in order to determine its roots.
Outcomes
At the end of this lesson you will be able to
- derive the quadratic formula using deductive reasoning
- solve a quadratic equation of the form ax2 + bx + c = 0 by applying the quadratic formula
- explain, using examples, how the discriminant may be used to determine whether a quadratic equation has two, one, or no real roots; and relate the number of zeros to the graph of the corresponding quadratic function
- select a method for solving a quadratic equation, justify the choice, and verify the solution
Lesson Questions
You will investigate the following questions:
- How is the quadratic formula related to the strategy of completing the square?
- How does a mathematical formula reveal the nature of the solutions to a problem?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 4 Assignment (Download the Lesson 4 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Module 4 Glossary Terms and Formula Sheet
- work under Project Connection
1.1. Launch
Module 4: Quadratic Equations and Inequalities
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? This section will help you find out.
Before beginning this lesson you should be able to
- isolate variables in equations
- determine the number of roots for a quadratic equation
1.2. Are You Ready?
Module 4: Quadratic Equations and Inequalities
Are You Ready?
Complete these questions. If you experience difficulty and need help, visit Refresher or contact your teacher.
- Rearrange the following equations to isolate the given variable.
- How many different roots can any given quadratic equation have? Answer
-
Solve each of the following quadratic equations by completing the square. Report answers as
- exact values
- decimals rounded to the nearest hundredth
How did the questions go? If you feel comfortable with the concepts covered in the questions, move on to Discover. If you experienced difficulties, use the resources in Refresher to review these important concepts before continuing through the lesson.
1.3. Refresher
Module 4: Quadratic Equations and Inequalities
Refresher
Use the following to review the topics you experienced difficulties with in the Are You Ready? section.
To review isolating variables in equations, read the definition and examples at Formula.
Use Solving Quadratic Equations: Using Graphs to review how to solve quadratic equations using graphs and how to relate these solutions to the zeros of their corresponding quadratic functions.
Go back to the Are You Ready? section and try the questions again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 4: Quadratic Equations and Inequalities
Discover

Try This 1
In this activity you will attempt to derive a formula that can be used to solve a quadratic equation. This formula will be derived by completing the square on the ax2 + bx + c = 0 form of a quadratic equation. You can work alone or with a classmate. It may be easier to work with someone else because you will be able to share ideas and strategies.
- The steps to find the exact value of the roots of the equation 2x2 + 3x + 4 = 0 are shown in the left column of the following table. In the right column, determine the exact value of the roots of the general equation ax2 + bx + c = 0 following the same steps used for the specific case. In the general case, you will not be able to simplify numbers since you will be working with unknown quantities. Just focus on the operations and don’t be concerned with the lack of numbers.
Specific Case
2x2 + 3x + 4 = 0General Case
ax2 + bx + c = 0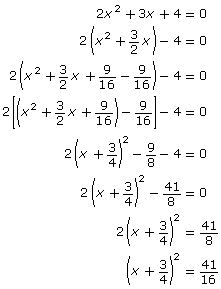
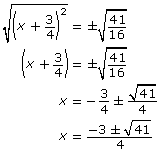
-
Look in the textbook or search the Internet for the quadratic formula. Compare the quadratic formula that you find to the roots you found for the general equation in the right column of question 1. Did you obtain the same formula by following the procedure above? If not, explain why not.
![]() Save your work in your course folder.
Save your work in your course folder.
You will have an opportunity to make any necessary revisions later in the lesson.
1.5. Explore
Module 4: Quadratic Equations and Inequalities
Explore

day time: © o2 Architecture. Reproduced with permission.; night time: © Blue Sky Homes. Reproduced with permission.
Prefabricated homes are houses whose sections are made in a factory. These sections are then shipped and assembled at the building site. A benefit of prefabricated homes is that most of the construction occurs in a controlled environment, such as a factory, that is protected from the weather and other elements. Another benefit is that the homes’ sections are standard shapes and sizes, which makes it easy to manufacture and assemble such homes in large quantities.
In this lesson you will solve quadratic equations using the quadratic formula. Just as the features of a prefab home can be customized to the specifications of a buyer, a formula is versatile and can be applied to any quadratic equation!
Here are some of the words you will want to define in Module 4 Glossary Terms in this lesson:
- quadratic formula
- discriminant
- deductive reasoning
1.6. Explore 2
Module 4: Quadratic Equations and Inequalities
Developing the Quadratic Formula
You derived the quadratic formula in Try This 1. You will now examine the formula’s development further. Retrieve your work from Try This 1. Open Developing the Quadratic Formula, which shows an approach that may look like the method you used in Try This 1.
To get to the applet, select The Quadratic Formula, and then select Developing the Quadratic Formula, under the Tutorial icon. Take your time to fully understand each step.
It can be confusing to manipulate algebraic expressions that contain multiple variables. A helpful technique is to work through a similar expression but substitute values for the variables a, b, and c. In this case, you could choose a quadratic equation such as 2x2 + 9x – 4 = 0 to solve by completing the square. This way you can see what happens to the numbers at each step.
You have seen that you can determine the roots of any quadratic equation of the form ax2 + bx + c = 0 by using this formula:
![]()
Add the quadratic formula to your copy of Formula Sheet.
Try This 2
Consider the quadratic equation 6x2 − 14x + 8 = 0.
- Use the quadratic formula to determine the roots of the equation.

- Verify the roots by substituting them, each in turn, into the original equations. Show that by doing so, the expression becomes zero and the equation is satisfied.
- What sorts of errors could a person make when using the quadratic formula? List any errors you found in your own work. If you didn’t have any errors, think of some places in the solution process where you would have to be careful.
![]() Save your work in your course folder.
Save your work in your course folder.
Turn to “Example 2” on page 248 in the textbook. Work through the solution process for both equations. Pay attention to the differences between the two solutions. The questions in green refer to a discriminant. What do you think the discriminant is? ![]()
Self-Check 1
Check your understanding by completing Quadratic Formula Self-Check.
This answer is important. Check your answer before moving on. The roots are ![]() and x = 1.
and x = 1.
Do your solutions match? If not, review your work to see where you might have made an error. You can turn to page 251 of the textbook to see how this equation can be solved with the quadratic formula. Then return to your original work to make corrections.
1.7. Explore 3
Module 4: Quadratic Equations and Inequalities
The Value of the Discriminant
Consider the expression underneath the radical in the quadratic formula, b2 − 4ac.
This expression is called the discriminant. In Try This 3 you will see how the value of the discriminant reveals the nature of the roots of the corresponding quadratic equation.
Try This 3
- Go to Quadratic Equations Table. For each of the equations, evaluate the discriminant. Then sketch the graph of the corresponding quadratic function and insert the graph into the table. Record the number and nature of the roots.
- Select several other quadratic equations from the textbook or make some equations up. Determine the discriminant of each of those equations. Sketch the graphs and determine the number and nature of the roots.
![]() Save your work in your course folder.
Save your work in your course folder.
Share 1
With a classmate, respond to the following questions.
- What values of the discriminant will result in two real and distinct roots?
- What value(s) of the discriminant will result in two real and equal roots?
- What values of the discriminant will result in no real roots?
- Why do you think the expression b2 − 4ac is called the discriminant?
![]() Save your work in your course folder.
Save your work in your course folder.
1.8. Explore 4
Module 4: Quadratic Equations and Inequalities
The Discriminant and the Roots of the Quadratic Equation
Watch The Discriminant: Three Cases to see how the value of the discriminant in the quadratic formula affects the roots of the corresponding quadratic equation.
Self-Check 2
Launch Discriminant Self-Check to practise determining discriminants and identifying the nature of the roots of different quadratic equations.
1.9. Explore 5
Module 4: Quadratic Equations and Inequalities
Selecting the Strategy for Solving the Quadratic Equation
So far in this module you have learned how to solve quadratic equations by a number of different strategies. These include the following:
- graphing
- factoring
- completing the square
- using the quadratic formula
The strategy that you use to solve any given quadratic equation will depend on the nature of the equation and the type of answer that is required, as well as on your own personal preference. In the next activity, you will work with a classmate to decide which strategies are best used to solve each of the quadratic equations that are given.
Share 2
- Work with a classmate to complete Strategies Chart. Then answer the questions 2 and 3 based on the information you gathered by completing Strategies Chart.
- Which method do you prefer? Give reasons for your answer.
- What are the advantages and disadvantages of each method? Summarize your answers in Advantages and Disadvantages Chart.
![]() Save your work in your course folder.
Save your work in your course folder.
Try This 4
An open box is constructed out of a sheet of cardboard measuring 24 in by 20 in. A square of unknown dimensions is cut out of each corner of the sheet to form the sides of the box. The base of the box has an area of 165 in2. Note: You will copy your answer to this question into your Lesson 4 Assignment later in the lesson.
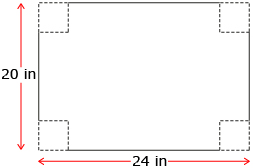
- Determine an expression for each of the dimensions of the base of the box.
- Set up an equation that can be used to determine the dimensions of each removed square.
- Determine the dimensions of the box.
![]() Save your work in your course folder.
Save your work in your course folder.
1.10. Explore 6
Module 4: Quadratic Equations and Inequalities
Example: Vegetable Garden
You are already familiar with modelling problems with quadratic equations. In this next exercise, you will see how a design question related to a vegetable garden can be modelled by a quadratic equation and then solved by using the quadratic formula. Work through The Quadratic Formula: Problem Situations. You will need to navigate to start by selecting The Quadratic Formula. Next, go to Examples by selecting the puzzle piece at the top of the window. Finally, choose Problem Situations.
Self-Check 3
Complete questions 8, 9, and 12 on pages 254 and 255 in the textbook. Answer
1.11. Connect
Module 4: Quadratic Equations and Inequalities
Open your copy of the Lesson 4 Assignment, which you saved in your course folder at the start of this lesson. Complete the assignment.
![]() Save all your work in your course folder.
Save all your work in your course folder.
Project Connection
Go to Module 4 Project: Imagineering. Complete Step 2: Feasibility Study.
![]() Save all your work in your course folder.
Save all your work in your course folder.
Going Beyond

Have you ever seen the humorous cartoon shown on the T-shirt in the illustration? Think you’ve got it easy when the discriminant shows that there are no real roots? After all, if there are no real roots, then there are no solutions, right? Not so fast. Mathematicians have a way of talking about such roots by introducing the concept of imaginary units. The imaginary unit, i, is defined as the square root of −1. In other words,
![]()
The following shows some examples of how you can simplify expressions involving the imaginary unit.
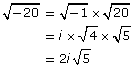 |
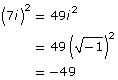 |
Solve the following quadratic equations that have no real roots.
- x2 + 4x + 10 = 0
- 5x2 − 2x + 1 = 0
If you pursue a career in engineering or mathematics or a science-related field, you may encounter imaginary units and complex numbers in your studies. You may want to search the Internet for information about these types of numbers and how they are applied in these different fields.
1.12. Lesson 4 Summary
Module 4: Quadratic Equations and Inequalities
Lesson 4 Summary
© treenabeena/13191894/Fotolia
In this lesson you investigated the following questions:
- How is the quadratic formula related to the strategy of completing the square?
- How does a mathematical formula reveal the nature of the solutions of a problem?
In this lesson you extended the strategy of completing the square to the development of the quadratic formula. By using the parameters a, b, and c, you were able to generalize a formula that could be applied to the solution of all quadratic equations. For any quadratic equation, ax2 + bx + c = 0, the exact roots can be determined by evaluating ![]() .
.
You discovered that by evaluating the discriminant b2 − 4ac, you could determine the nature of the roots. The following table summarizes these results.
| Discriminant | Nature of Roots |
| b2 − 4ac > 0 | two distinct and real roots |
| b2 − 4ac = 0 | one distinct or two real and equal roots |
| b2 − 4ac < 0 | no real roots |
In the second half of this module, you will study systems of quadratic and linear equations. You will build on what you learned in previous math courses as well as what you have learned about solving quadratic equations. You will work closely with graphs as you complete this module.