Lesson 1
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-1 SS |
| Book: | Lesson 1 |
| Printed by: | Guest user |
| Date: | Thursday, 4 December 2025, 2:15 AM |
Description
Created by IMSreader
1. Lesson 1
Module 6: Rational Expressions
Lesson 1: Simplifying Rational Expressions
Focus

c Sergey Khantsis; Used under Creative Commons Licence 2.5- Share, Adapt, Attribution
Flight simulators are practical training tools for people learning to be pilots. These simulators mimic actual flying conditions. Flight students must control the plane using equipment and instrumentation similar to what is found in real aircraft.
Driving simulators are used in rehabilitation hospitals to help people who have been injured learn how to drive again. Simulators provide a safe environment for learning how to navigate different scenarios that may be encountered in real life. The simulated experience is equivalent to the real one in many ways, but the simulated experience is simplified for training purposes. Can you think of other examples of simulations? What types of situations are being simulated?
In previous math courses you worked with rational numbers. The strategies you used to generate equivalent fractions and to simplify fractions will help you to do the same processes with rational expressions. Your previous experience with rational numbers can be thought of as the training for, or simulation of, the work you will do with rational expressions in this lesson and module.
Outcomes
At the end of this lesson you will be able to
- compare the strategies for writing equivalent forms of rational expressions to the strategies for writing equivalent forms of rational numbers
- determine the non-permissible values for a rational expression and explain why such values are non-permissible
- determine equivalent rational expressions to given rational expressions and explain why the non-permissible values of both are the same
- simplify a rational expression and identify, correct, and explain errors in the simplification of a rational expression
Lesson Questions
You will investigate the following questions:
- How is the process of simplifying rational expressions similar to the process of simplifying rational numbers?
- Why is simplification desired in mathematics?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 1 Assignment (Download the Lesson 1 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Module 6 Glossary Terms and Formula Sheet
- work under Project Connection
Self-Check activities are for your own use. You can compare your answers to suggested answers to see if you are on track. If you are having difficulty with concepts or calculations, contact your teacher.
1.1. Launch
Module 6: Rational Expressions
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? This section, which includes Are You Ready? and Refresher, will help you find out.
Before beginning this lesson you should be able to
- define rational numbers
- write equivalent fractions
- determine the greatest common factor (GCF) of a set of numbers
- simplify fractions
1.2. Are You Ready?
Module 6: Rational Expressions
Are You Ready?
Complete the following questions. If you experience difficulty and need help, visit Refresher or contact your teacher.
- What is a rational number? Answer
- Complete each statement so that the fractions are equivalent.
- Determine the prime factorization of each expression.
- Simplify the following fractions.
How did the questions go? If you feel comfortable with the concepts covered in the questions, skip forward to Discover. If you experienced difficulties, use the resources in Refresher to review these important concepts before continuing through the lesson.
1.3. Refresher
Module 6: Rational Expressions
Refresher
Review the definition and work through the demonstration applet in Rational Numbers.
Review examples of writing and simplifying fractions in Equivalent Fractions.
Greatest Common Factor (GCF) provides a definition to review and an applet to explore factors and greatest common factors.
Go back to the Are You Ready? section and try the questions again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 6: Rational Expressions
Discover

© Rob Byron/3683987/Fotolia
In this section you will play a game to discover something about rational expressions.
Try This 1
Follow the steps in Table 1.
TABLE 1 |
|
| Step | Instruction |
| 1 | Pick any number. |
| 2 | Square the number. |
| 3 | Subtract 4 from the result. |
| 4 | Divide the result by two more than the original number. |
-
How does the final result compare to the original number?
- Repeat the procedure with a different starting number each time. What do you notice?
- Copy Table 1, and add a third column, as shown, called “Expression.” Write an expression for each step in the table beginning with the expression “x”.
TABLE 1
Step Instruction Expression 1 Pick any number. x 2 Square the number. 3 Subtract 4 from the result. 4 Divide the result by two more than the original number.
-
Based on your answers to questions 1 and 2, what is another expression that could be used to represent the final result?
- There is one starting number that does not yield a result similar to the other results. Can you determine this number?
![]() Save your responses in your course folder.
Save your responses in your course folder.
You will need to retrieve these results later in the lesson in order to check your work and to share what you have learned with a classmate.
1.5. Explore
Module 6: Rational Expressions
Explore
Do you have a favourite board game? Perhaps you like classic games, such as Monopoly, The Game of Life, or Snakes and Ladders! Two important principles of game design are realism and simplicity. Part of what makes these games enjoyable is the fact that they simulate real-world contexts. In the examples provided here, one is a real-estate trading game, another takes you through the milestones of life, and the third simulates life with ladders rewarding good acts and snakes penalizing bad acts.
What really makes these games fun and engaging is that they portray realistic situations and have rules that young children can understand. For example, gameplay in Monopoly is not bogged down by housing inspections or lawyer fees that would normally come with every real-life property purchase. These aspects, though realistic, would complicate the game and reduce the game’s entertainment value.
In this lesson you will study rational expressions. Just like a game designer creates games based on reality, you will learn how to write algebraic expressions that are equivalent to other expressions. As well, just as games are simplified versions of the real thing, you will learn to simplify rational expressions.
![]() Save Module 6 Glossary Terms in your course folder now.
Save Module 6 Glossary Terms in your course folder now.
Here are some of the words you will want to define in Module 6 Glossary Terms in this lesson:
- rational expression
- non-permissible value
- restriction
1.6. Explore 2
Module 6: Rational Expressions
Rational Expressions
Recall the definition of a rational number: a real number that can be expressed in the form ![]() , where a and b are integers and b ≠ 0.
, where a and b are integers and b ≠ 0.
A rational expression has a similar definition. A rational expression can be expressed in the form of ![]() , where a and b are polynomials and b ≠ 0.
, where a and b are polynomials and b ≠ 0.
Retrieve your work from Try This 1. In that activity you picked a number and applied a series of mathematical operations to the number. You should have obtained the following rational expression to describe the result:
![]()
You may have noticed that the result is always two less than the original number. For example, if you started with the number 19, your final result was 17. You may have also determined that there was one number that does not follow this pattern.
Share 1
Confirm that x = −2 does not yield the same result as any other value of x. You may want to use a calculator to do this. What does your calculator show when a rational expression is undefined?
With a classmate discuss why x = −2 does not follow the same pattern.
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.7. Explore 3
Module 6: Rational Expressions
Non-Permissible Values
A rational expression is not defined when the expression’s denominator is zero. Therefore, any value of the variable that would result in a denominator of zero is considered a non-permissible value.
Try This 2
For each of the rational expressions in the table, determine the non-permissible value(s). You can check your answers by using your calculator.
| Rational Expression | Non-Permissible Value(s) of x |
![]() Save your response in your course folder.
Save your response in your course folder.

Turn to “Example 1” on page 312 in the textbook to see how you can determine non-permissible values for rational expressions that are similar to the expressions in Try This 2. Look for answers to the following questions:
- What equations are used to find non-permissible values?
- Why is it not necessary to determine when numerators are equal to zero?
- How does factoring the denominator make it easier to identify non-permissible values?
Look back at your answers to Try This 2. After reading through “Example 1,” are there any answers you would change? Why?
Self-Check 1
Complete Non-Permissible Values Self-Check to check your understanding of the concepts presented so far.
1.8. Explore 4
Module 6: Rational Expressions
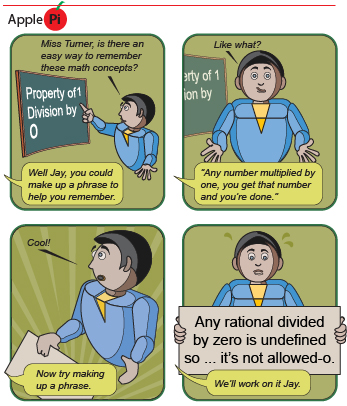
The Property of 1
What happens to a number if you multiply the number by 1? If you said that the number remains unchanged, you are absolutely right. This property of one is critical in determining equivalent expressions in mathematics.
Try This 3
- Multiply or divide the following numbers.
- Verify that the end result for each of the calculations in question 1 is equivalent. You may want to do this by using your calculator to check that the decimal representation of the original number is identical to that of the final number.
- To what number are

 and
and  equivalent?
equivalent?
- Compare the following two expressions:
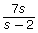 and
and 
- Identify the non-permissible value(s) for s in each expression.
- Are the expressions equivalent? How do you know?
- Identify the non-permissible value(s) for s in each expression.
![]() Save your responses in your course folder.
Save your responses in your course folder.
You will use your responses to question 1 to complete Share 2, Part B.
Generating Equivalent Rational Expressions
Turn to page 313 in the textbook. Read the section “Equivalent Rational Expressions” for an explanation of how to generate equivalent expressions. As you follow the process that takes a rational expression to an equivalent expression, think about how you could reverse the process.
How could you take the equivalent expression and convert the expression back to the original rational expression?
![]() Record your ideas in your course folder. You will look at this process again later in the lesson.
Record your ideas in your course folder. You will look at this process again later in the lesson.
Cross Multiplying to Confirm Equivalent Expressions
The product of any number and 1 is the number itself. Although the product may look very different, the product is, in fact, equivalent to the original number.
As revealed in Try This 3, to generate equivalent expressions, you simply multiply both the numerator and denominator by the same value.
To confirm that two expressions are equivalent, simply use the cross-product method.
If ![]() then ad = bc.
then ad = bc.
Here is the proof. Multiply both sides by the common denominator bd; then simplify the expression.

Therefore, if ![]() then ad = bc.
then ad = bc.
1.9. Explore 5
Module 6: Rational Expressions
Simplifying Rational Expressions
![]()
To simplify a rational expression means to write an equivalent expression where the greatest common factor between the numerator and the denominator is 1. Such an expression is described as being in simplified form, or reduced to lowest terms.
The following example shows how you can simplify a rational number by using the method of prime factorization. Pay careful attention to the steps of this example. You will apply these steps to rational expressions in Try This 4.
Example
- Simplify
 by using prime factorization.
by using prime factorization.
- Verify that the simplified form is equivalent to the original rational number.
Solution
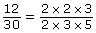
By rearranging the order of the factors in the numerator, the expression can be written as the product of three fractions.
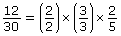
Since the first two fractions are equal to 1, the expression is simplified to

Therefore, according to the property of 1, where any number multiplied by 1 is equal to itself,
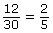
- You can use cross-products to verify that
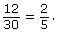
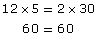
Since the cross-products are equal,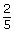 is equivalent to
is equivalent to 
1.10. Explore 6
Module 6: Rational Expressions
In Try This 1 you found that by applying a series of mathematical operations to a number, you end up with a number that is two less than the original number. The following statement summarizes this observation.
![]()
The expression ![]() is equivalent to the expression x − 2 for all values of x, except when x = −2.
is equivalent to the expression x − 2 for all values of x, except when x = −2.
In Try This 4 you will use the same principles demonstrated in the previous example to confirm this result.
Try This 4
- Consider the rational expression
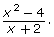 Show that this expression simplifies to x − 2.
Show that this expression simplifies to x − 2.




- Simplify the rational expression
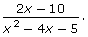 State any non-permissible values.
State any non-permissible values.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 2
Part A: Discussion
Discuss the following questions with a partner. Record your responses.
- What are some key differences between simplifying rational numbers and simplifying rational expressions?
- Why is it necessary to include the non-permissible value(s) with the simplified form even though this form may not have a denominator?
- Based on your answer to question 2, when should you identify non-permissible values?
Part B: Calculator Verification
You can use your graphing calculator to verify that two expressions are equivalent. Follow the steps outlined below for each of three rational expressions and their simplified forms. Use the following rational expressions and the equivalent expressions you obtained in Try This 3 question 1:
Step 1: Input the rational expression into Y1 of the Y= editor.
Step 2: Input the other rational expression into Y2 of the Y= editor. If you have the option to do so, set the graph to a different thickness.
Step 3: Graph the expressions. If the first expression graphs over the second expression, you have confirmed that the expressions are the same.
Discuss the following questions in relation to the calculator verification procedure.
- The graphs should appear to be identical. In fact, they are not. Can you identify where the two graphs are not identical and give an explanation as to why this is the case?
- How can you recognize when two rational expressions that appear to be identical are, in fact, not identical?
![]() Save your responses in your course folder.
Save your responses in your course folder.
Your teacher may wish to check your answers to ensure you have a good grasp of the material learned so far.
1.11. Explore 7
Module 6: Rational Expressions
Try This 5
Turn to “Example 3” on page 315 of the textbook to see how you can simplify a rational expression consisting of two variables. As you work through the solution, answer these questions:
- What methods are used to factor the numerator and denominator?
- How are the examples of non-permissible values determined?
- How do you determine an expression for the non-permissible values of y?
- Which method do you prefer for completing part c? Why?
![]() Save your responses in your course folder.
Save your responses in your course folder.
Self-Check 2
With a partner, play Simplify Rational Expressions. Each of you will answer a set of math questions. When you’re done, compare your answers. Your answers should match in each row. If your answers do not match, work together to figure out where you went wrong. Answer
![]() Save your responses in your course folder.
Save your responses in your course folder.
Factoring the Numerator and the Denominator
When you encounter a rational expression where both the numerator and denominator must be factored before the expression can be simplified, it is likely that they will share a common factor. You can use this knowledge to factor more easily.
For example, suppose you are required to simplify the following rational expression:
![]()
Step 1: Start by factoring the simpler of the two polynomials in the numerator and denominator. In this case, factor the numerator.
![]()
Step 2: Since the numerator has a binomial factor of (x + 3), there is a chance that the denominator will also have the same factor. If so, you will have the following:
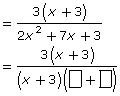
Step 3: By inspection, you can determine the terms of the second binomial factor.
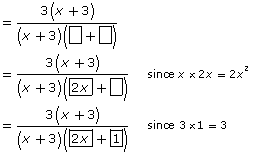
Step 4: You should check that 2x + 1 is the second factor by multiplying (x + 3)(2x + 1). In this case, the product is 2x2 + 7x + 3. Therefore, the correct factors are (x + 3) and (2x + 1).
1.12. Explore 8
Module 6: Rational Expressions
Watching for Errors
Thus far in the lesson, you have learned how to write equivalent rational expressions and reduce the expressions to lowest terms. In the remainder of the lesson you will study errors that can occur in the process of simplifying rational expressions. You will do this by analyzing the work of fictional students.
Try This 6
The work of four different students is shown. Each student has made an error in simplifying certain rational expressions.
- Analyze the work of each student.
- Identify and explain the error.
- Show the correct solution.
- Marlee
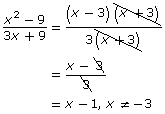
- Neetu
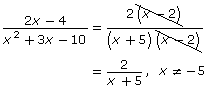
- Aaron

- Siobhan
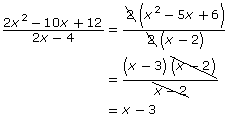
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 3
With a classmate, compare your answers to Try This 6. Discuss how the errors you identified can be avoided. In other words, are there strategies that can be applied so that the risk of making the mistakes is minimized?
![]() Save your responses in your course folder.
Save your responses in your course folder.
Make any necessary revisions to your work from Try This 6. You will be asked to copy your work from Try This 6 into the Lesson 1 Assignment later in this lesson.
Self-Check 3
Turn to page 318 in the textbook to practise identifying and correcting errors in simplifying rational expressions. Complete questions 7, 9, 10, 11, and 13. Answer
1.13. Connect
Module 6: Rational Expressions
In the Lesson 1 Assignment you will demonstrate your understanding of the lesson outcomes. You will apply the concepts and strategies you learned to new situations. You must show your work to support your answers.
Open your copy of Lesson 1 Assignment, which you saved in your course folder at the beginning of this lesson. Complete the assignment.
![]() Save all your work in your course folder.
Save all your work in your course folder.
Project Connection
In Module 6 Project: Game Challenge, you will design and analyze games for a reality show. In the first phase of the project, you will research and brainstorm ideas for different games.
Go to Module 6 Project: Game Challenge. Read all parts of the Module 6 Project as an overview of what you will be doing to complete the project. Complete Step 1.
![]() Save all your work in your course folder.
Save all your work in your course folder.
Going Beyond
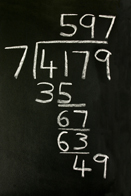
© Sharpshot/2754084/Fotolia
Do you remember how to divide numbers by long division? The image shows the long division of 4179 by 7. The quotient is 597. Study the image in order to review the process.
Did you know that you can also apply long division to polynomials?
In this lesson you simplified expressions, such as ![]() , by removing factors common to the numerator and the denominator. Long division is another method you can use to simplify rational expressions.
, by removing factors common to the numerator and the denominator. Long division is another method you can use to simplify rational expressions.
Part A
Compare the long division of rational numbers as shown in the image versus the long division of polynomials shown here:
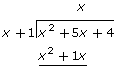
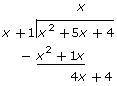
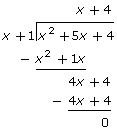
Answer the following questions:
- Where do you look for the simplified form of the original rational expression?
- Notice that the remainder is 0. What does that mean? What would it mean if the remainder were not equal to 0?
- Where do you look to find non-permissible values?
Part B
- Return to some of the questions you completed in this lesson. Use the method of long division to see if your answers match. Are there rational expressions that are better simplified with the long-division method? Are there expressions that are difficult to simplify with this method?
![]() Save your work in your course folder.
Save your work in your course folder.
1.14. Lesson 1 Summary
Module 6: Rational Expressions
Lesson 1 Summary

You investigated the following questions:
- How is the process of simplifying rational expressions similar to the process of simplifying rational numbers?
- Why is simplification desired in mathematics?
You discovered that simplifying rational expressions is similar to simplifying rational numbers. In both cases, you must find factors common to both the numerator and the denominator. It is appropriate to eliminate these common factors according to the property of 1.
The property of 1 states that the multiplication of any number by 1 is equal to itself. Therefore, eliminating factors common to both the numerator and the denominator results in an equivalent, but simplified, expression.
You discovered a significant difference between simplifying rational numbers and simplifying rational expressions. In the case of rational expressions, you must consider non-permissible values. Any value(s) of the variable that would result in a denominator equal to zero is considered non-permissible.
The process of simplifying is an essential skill that should be part of any math student’s repertoire. Simplifying expressions allows you to simplify calculations, especially those that involve multiple steps. Reducing the size of the numbers and the amount of variables that you must carry from step to step makes subsequent calculations easier and reduces the risk of errors. In the next two lessons you will confirm this claim as you multiply, divide, add, and subtract rational expressions.