Lesson 2
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-1 SS |
| Book: | Lesson 2 |
| Printed by: | Guest user |
| Date: | Thursday, 4 December 2025, 2:12 AM |
Description
Created by IMSreader
1. Lesson 2
Module 6: Rational Expressions
Lesson 2: Multiplying and Dividing Rational Expressions
Focus

© Tilio & Paolo/18284919/Fotolia
What’s your favourite game or sport that is played on a court? Basketball, volleyball, and tennis are played on courts. Most court sports are team games, where members of the same team co-operate to score points against the other team. Some of these games may also be played without the co-operative aspect and instead be played one-on-one.
Jai alai is a sport with Spanish origins played on a large rectangular court called a fronton. The court consists of a floor that can extend up to 200 ft in length and includes three wall surfaces. Players in jai alai bounce a special ball off the front wall using a custom-made basket that is attached to the wrist. A player earns a point if the opponent fails to catch the ball when it rebounds. Known as the fastest sport on Earth and also described as “ballet with bullets,” jai alai is a sport that can be played one-on-one or with pairs.
In this lesson you will learn how to multiply and divide rational expressions. You will use rational expressions to model the dimensions of the courts in various sports and games, including jai alai.
Outcomes
At the end of this lesson you will be able to
- compare the strategies for multiplying and dividing rational expressions to the strategies for multiplying and dividing rational numbers
- determine the non-permissible values when multiplying and dividing rational expressions
- determine, in simplified form, the product or quotient of rational expressions
Lesson Questions
You will investigate the following questions:
- How are multiplying and dividing rational expressions similar to multiplying and dividing rational numbers?
- How are non-permissible values determined when multiplying and dividing rational expressions?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 2 Assignment (Download the Lesson 2 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Module 6 Glossary Terms and Formula Sheet
- work under Project Connection
1.1. Launch
Module 6: Rational Expressions
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? This section, which includes Are You Ready? and Refresher, will help you find out.
Before beginning this lesson you should be able to
- multiply fractions
- divide fractions
1.2. Are You Ready?
Module 6: Rational Expressions
Are You Ready?
Complete the following questions. If you experience difficulty and need help, visit Refresher or contact your teacher.
- How do you multiply fractions? Answer
- Multiply the following fractions. Simplify where possible.
- How do you divide fractions? Answer
- Divide the following fractions. Simplify where possible.
How did the questions go? If you feel comfortable with the concepts covered in the questions, skip forward to Discover. If you experienced difficulties, use the resources in Refresher to review these important concepts before continuing through the lesson.
1.4. Discover
Module 6: Rational Expressions
Discover
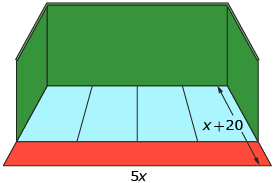
An illustration of a jai alai court is shown. The court consists of three walls shown in green, an in-bounds floor area divided into four sections, and an out-of-bounds area shown in red. The length and width of the court can be modelled by the illustration shown.
The width of each section of the floor area is seven-tenths the width of the court. The length of each section is approximately one-quarter the length of the court.
Try This 1
- Write an expression that represents the total court area, including the out-of-bounds area. Remember area = length × width.
- Write an expression that represents each of the following dimensions of the court:
- the length of a blue section of the court floor (matches the length of a short green wall)
- the width of one blue section (matches a part of the long green wall)
- the area of one blue section
- the length of a blue section of the court floor (matches the length of a short green wall)
-
- Write a rational expression that represents the fraction of the total court area occupied by one blue section.
- Simplify this expression.
- Write a rational expression that represents the fraction of the total court area occupied by one blue section.
- If x = 30 ft in the illustration, determine the area of one blue section using
- the expression in 2.c.
- the expressions for the dimensions (length and width) of the entire court and applying the original information about the length and width of one blue section
- the expression in 2.c.
- Compare your results in 4.a. and 4.b.
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.5. Explore
Module 6: Rational Expressions
Explore

© Jesse-lee Lang/14521330/Fotolia
You may often find familiar elements in science fiction books and films that depict futuristic worlds. For example, in the film Tron: Legacy (2010), silicon-based gladiators battle each other in a game that is reminiscent of jai alai or racquetball. The gladiators throw glowing discs at each other with the intention of terminating the opponent. Like jai alai, the discs rebound off the surrounding walls until they are either caught or hit their mark. The discs are thrown with great speed, and, again as in jai alai, the gladiators undergo dazzling acrobatic maneuvers in order to score points.
Just as many aspects of science fiction are based on familiar themes, so too will you find the same concepts recurring in mathematics. In this lesson you will discover that multiplying and dividing rational expressions is identical to multiplying and dividing rational numbers, with one exception. Do you know what this exception is?
Here is one of the terms you will want to define in Module 6 Glossary Terms in this lesson:
- complex rational expression
1.6. Explore 2
Module 6: Rational Expressions
In the Launch section of this lesson, you reviewed how to multiply rational numbers. In the general case, recall that
![]()
Notice that the numerators are multiplied together and that the denominators are multiplied together. The result is then reduced to lowest terms, where possible.
Retrieve your results from Try This 1. The answers to questions 4.a. and 4.b. should have been the same. That result leads to the conclusion that rational expressions are multiplied and divided in the same way as rational numbers. In other words, numerators are multiplied together and denominators are multiplied together. The resulting expression is then simplified, where possible.
In Try This 2 you will multiply each set of rational expressions. Remember to include the non-permissible values!
Try This 2
Multiply the rational expressions as you would rational numbers. Reduce to lowest terms, where possible. Include the non-permissible values with your final answer.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 1
Compare your answers and strategies from Try This 2 with a partner. Discuss the following questions with your partner.
- What do all of the expressions in Try This 2 have in common?
- How are the expressions in Try This 2 different from the following expression?

- How could you simplify the multiplication process in order to obtain the product of the expression in question 2?
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.7. Explore 3
Module 6: Rational Expressions
Turn to “Example 1” on page 324 of your textbook. This example shows a multiplication expression that is similar to the one you encountered at the end of Share 1. Work through the example to confirm your discussion in Share 1. Focus on the steps you would take, particularly the first step, to be able to efficiently multiply and simplify the product.
Try This 3
Retrieve your notes from Share 1. Multiply the expression given using the method presented in the example. You should obtain a constant of 2 if you simplify correctly. You should also obtain two non-permissible values.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Self-Check 1
Check your understanding of the concepts presented so far by completing Multiplying Rational Numbers Self-Check.
You have just learned how to multiply rational numbers. Recall that dividing rational numbers is a process that involves multiplying the first number by the reciprocal of the second number.
How does the division of rational expressions compare with the division of rational numbers? In Try This 4 you will explore both procedures.
Try This 4
- Solve
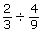 without using your calculator.
without using your calculator.
- Describe a procedure for solving
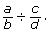 You may want to revisit your answer to question 3 in the Are You Ready? section.
You may want to revisit your answer to question 3 in the Are You Ready? section.
- Apply the same procedure described in question 2 to determine the quotient of each of the following expressions:
- How can you verify your answers to question 3?
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 2
Compare your results from Try This 4 with a partner, and discuss the following questions.
- When dividing rational expressions, where should you look in order to determine the non-permissible values? Is it sufficient to look at the denominators only?
- In question 3 you divided rational expressions that had a common denominator. Consider the expression
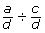 . What is the result when the expression is simplified? Can you and your classmate uncover a pattern to describe a short cut that leads to the same answer?
. What is the result when the expression is simplified? Can you and your classmate uncover a pattern to describe a short cut that leads to the same answer?
1.8. Explore 4
Module 6: Rational Expressions
Turn to page 325 in your textbook. Read “Dividing Rational Expressions,” above “Example 2.” Examples are shown using both rational numbers and rational expressions. As you read this section, think about the relative benefits and drawbacks of each method shown. Answer the following questions:
- Is one method better for identifying non-permissible values?
- Which method do you prefer? Explain why.
- Notice that the x-variable appears in neither the denominator in the original expression nor in the denominator in the final simplified form. Yet x ≠ 0. In other words, x = 0 is a non-permissible value. What does this tell you about how you should identify non-permissible values?
Dividing rational expressions is similar to dividing rational numbers. One difference is that, in the case of rational expressions, you must state the non-permissible values.
When dividing rational expressions, however, the non-permissible values must be determined by considering where the denominators of the original expression are equal to zero. To be sure that you have included all non-permissible values, you must consider the denominators of the simplified form and the denominators throughout the division process. Keep this in mind as you proceed to the next activity.
Try This 5
- Solve the following rational expression.

- Identify the non-permissible values.
Refer to “Example 2” on page 325 of your textbook to confirm that you correctly simplified and identified all of the non-permissible values.
![]() Save your response in your course folder.
Save your response in your course folder.
Did You Know?
A complex rational expression is a rational expression that contains rational expressions in the numerator and/or denominator. Here is an example:

A complex rational expression doesn’t have to be intimidating! You can write the preceding example in the following way:
![]()
You can then factor and simplify as usual.
Share 3
With a classmate, discuss the following points related to Try This 5.
- Why is it important to factor any second-degree polynomial?
- Where do you look for non-permissible values?
- Why are division expressions first converted to multiplication expressions before simplifying?
![]() Save your response in your course folder.
Save your response in your course folder.
Self-Check 2
Complete Dividing Rational Numbers Self-Check.
1.9. Explore 5
Module 6: Rational Expressions
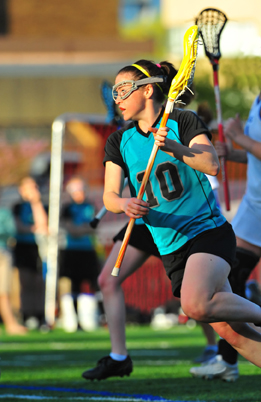
Hemera/Thinkstock
You have now learned how to multiply and divide rational expressions. In the final section of this lesson you will consider an application of rational expressions in the sport of lacrosse.
Lacrosse, like jai alai, is a sport where players toss the game ball using sticks with baskets on the ends. Lacrosse has origins in aboriginal culture. In Self-Check 3 you will analyze the dimensions of a lacrosse field using rational expressions.
Self-Check 3
- The diagram shows the layout of a lacrosse field. The area outlined in white is called the goal area. The location of the goal is marked by the circle in the goal area.

- Complete questions 11, 14, 15, and 16 on page 328 in the textbook. Answer
1.10. Connect
Module 6: Rational Expressions
Open your copy of Lesson 2 Assignment, which you saved in your course folder at the beginning of this lesson. Complete the assignment.
![]() Save your work in your course folder.
Save your work in your course folder.
Project Connection
Go to Module 6 Project: Game Challenge. Complete Step 2.
![]() Save your work in your course folder.
Save your work in your course folder.
Going Beyond
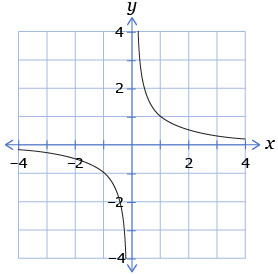
Did you know that you can graph rational expressions? The graph of ![]() is shown.
is shown.
- Consider the rational expression
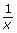 . What is the non-permissible value of
. What is the non-permissible value of 
- How is the non-permissible value from question 1 reflected in the graph of
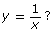
- Graph the function
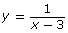 using graphing technology. How is the non-permissible value of this function reflected in its graph?
using graphing technology. How is the non-permissible value of this function reflected in its graph?
- Graph the function
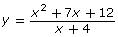 using graphing technology.
using graphing technology.
- How is the non-permissible value of this function reflected in the graph?

- How is the representation of the non-permissible value for
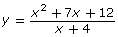 different from the representation of the non-permissible value for
different from the representation of the non-permissible value for  and
and 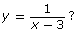
- Simplify the expression

- What is the difference between the graph of
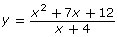 and the graph of y = x + 3?
and the graph of y = x + 3?
- How is the non-permissible value of this function reflected in the graph?
You will further explore rational functions in the your next math course. Save your work in your course folder. You may also want to save your work in a separate folder in case you want to access your notes in your next math course.
1.11. Lesson 2 Summary
Module 6: Rational Expressions
Lesson 2 Summary

Jim Rogash/Getty Images
In this lesson you investigated the following questions:
- How is multiplying and dividing rational expressions similar to multiplying and dividing rational numbers?
- How are non-permissible values determined when multiplying and dividing rational expressions?
In this lesson you learned about the similarities between multiplying and dividing rational expressions and multiplying and dividing rational numbers. In both cases, you must multiply numerators with numerators and denominators with denominators. At some point during the process, you must also simplify the result. You discovered that obtaining a simplified result is more easily done when the polynomial expressions in the numerator and denominator are factored first.
One aspect of multiplying and dividing rational expressions that does not emerge in multiplying and dividing rational numbers is the need to determine non-permissible values. You must identify those values of the variable(s) that would result in a zero denominator as non-permissible.
When dividing rational expressions, you must also consider the numerator of the divisor (or the second fraction). Since the numerator is reciprocated in the course of division, you must also identify as non-permissible the value(s) of the variable(s) that would render the numerator equal to zero.
In the next lesson you will compare the addition and subtraction of rational expressions to the addition and subtraction of rational numbers.



