Lesson 4
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-1 SS |
| Book: | Lesson 4 |
| Printed by: | Guest user |
| Date: | Thursday, 4 December 2025, 2:08 AM |
Description
Created by IMSreader
1. Lesson 4
Module 6: Rational Expressions
Lesson 4: Solving Rational Equations
Focus

iStockphoto/Thinkstock
Many reality television shows are based on competition between individuals or teams of people. Contestants compete in challenges for the right to remain in the game. Challenges may involve navigating an obstacle course, solving a puzzle, finding a hidden object, or any combination of these or other tasks.
In a way, solving equations in mathematics is similar to these tasks. When solving equations you often have to navigate through several steps in order to find the unknown variable, or the “hidden object.”
In this lesson you will learn to solve rational equations. You will learn basic principles that will help you tackle a wide variety of problems.
Outcomes
At the end of this lesson you will be able to
- determine the non-permissible values for the variable in a rational equation
- determine the solution to a rational equation algebraically, and explain the process used to solve the equation
- explain why a value obtained in solving a rational equation may not be a solution of the equation
Lesson Questions
You will investigate the following questions:
- What principles are common to the strategies for solving rational equations and how are these principles helpful?
- Why are some values of the variable obtained in solving rational equations not roots of the equations?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 4 Assignment (Download the Lesson 4 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Module 6 Glossary Terms and Formula Sheet
- work under Project Connection
1.1. Launch
Module 6: Rational Expressions
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? This section, which includes Are You Ready? and Refresher, will help you find out.
Before beginning this lesson you should be able to
- determine the LCD
- solve linear and quadratic equations
1.2. Are You Ready?
Module 6: Rational Expressions
Are You Ready?
Complete the following questions. If you experience difficulty and need help, visit Refresher or contact your teacher.
- Determine the lowest common denominator.
- Solve the following equations.
How did the questions go? If you feel comfortable with the concepts covered in the questions, skip forward to Discover. If you experienced difficulties, use the resources in Refresher to review these important concepts before continuing through the lesson.
1.3. Refresher
Module 6: Rational Expressions
Refresher
Three resources are recommended for reviewing how to determine the lowest common denominator (LCD).
Watch “Adding and Subtracting Rational Expressions 2.” Pay attention to how the lowest common denominator is found. In the video, the question includes stating the domain, which is another way of asking for the non-permissible values.
Watch “Adding and Subtracting Rational Expressions 3.” Pay attention to how the lowest common denominator is found.
You can also review finding the LCD by returning to Lesson 3.
Two resources are recommended to review how to solve linear and quadratic equations.
Watch “Algebra: Linear Equations 4.”
Watch “Solving Quadratic Equations by Factoring” to review a solution to a quadratic equation.
Go back to the Are You Ready section and try the questions again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 6: Rational Expressions
Discover

Goodshoot/Thinkstock
Try This 1
| Equation A | Equation B | Equation C |
| 0.125x + 0.25x = 6 | 3x + 6x = 144 | |
- Consider the three equations in the table. Solve each of the equations in the cell below each equation. Begin with the equation you think would be the easiest to solve. Show all of your work.
- What do you notice about the root of each equation?
- What is the relationship between the three equations?
- How can you convert between each of the following equations?
- Equation A to Equation C
- Equation A to Equation B
- Equation A to Equation C
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.5. Explore
Module 6: Rational Expressions
Explore

c krabata/22361180/Fotolia
Consider the puzzle shown. What aspects of puzzles make them challenging to assemble? What aspects make them easy to assemble? Can you tell what strategies might have been used to assemble the puzzle in the image?
What strategies do you use when tackling difficult puzzles? Do you begin by assembling the border? Do you collect certain pieces that have the same colour or that may be used to create distinct parts of the puzzle? These strategies and others can help to reduce a pile of random puzzle pieces into a beautiful picture.
In this lesson you will learn how to solve rational equations. Like your approach to a puzzle, you can use strategies to make unraveling the final picture—the solution—much easier.
Here are some of the terms you will want to define in your copy of Module 6 Glossary Terms in this lesson:
- rational equation
- extraneous root
- clear the denominator
1.6. Explore 2
Module 6: Rational Expressions
Solving Rational Equations
A rational equation is an equation that contains rational expressions.
| Examples of Rational Equations | ||
To solve a rational equation you must isolate the unknown variable, just as you would to solve any other equation. Since you need to eliminate the denominators, there is an extra step in solving rational equations.
Retrieve your work from Try This 1. In that activity you discovered that each of the three equations had the same root. This is because the three equations are equivalent. In other words, you can determine the answer to Equation A by solving Equation B or Equation C.
Equation B and Equation C were easier to solve because they did not contain rational expressions. Generally speaking, an equation is easier to solve when you don’t have to work with denominators!
In Try This 1 you explored personal strategies for converting between different equation types. In this lesson you will mostly use the lowest common denominator to clear the denominators.
Try This 2
Consider the following rational equation:
![]()
- Determine the non-permissible value(s).
- Determine the lowest common denominator.
- Multiply the expression on each side of the equation by the LCD.
- Solve the resulting equation for x.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 1
Compare your answers to Try This 2 with a partner. Discuss any discrepancies in the solution process and in the result. Come to an agreement on how to resolve any discrepancies. Then discuss the following questions based on Try This 2.
- What was the purpose of the step in question 3?
- Do you have to use the LCD to determine the correct answer? Give reasons to support your answer.
- Why is it important to determine the non-permissible value(s) at the beginning of the solution process instead of waiting until the end?
- In this case, the non-permissible value is different from the final answer. What if you ended up with a final answer that was equal to a non-permissible value? Would this be possible?
![]() Save your responses in your course folder.
Save your responses in your course folder.
As you proceed through this lesson, you may wish to return to these responses to make revisions as your understanding of concepts deepens. Your teacher may wish to check your responses.
1.7. Explore 3
Module 6: Rational Expressions
Using Cross Multiplication
![]()
A short-cut strategy for solving rational equations of the form ![]() is to solve the equivalent equation ad = bc. If you are not convinced this shortcut works, choose two fractions that you know are equivalent and try the short cut.
is to solve the equivalent equation ad = bc. If you are not convinced this shortcut works, choose two fractions that you know are equivalent and try the short cut.
For example, is ![]() the same as 2(6) = 3(4)?
the same as 2(6) = 3(4)?
Try this short cut on the rational equation in Try This 2.
When you have seen that the short cut works, figure out why it works. If you can figure out how the rational equation is equivalent to ad = bc, you will have figured out why the short cut works.
Work through Rational Equations to practise applying the steps in solving rational equations. Select the tutorial icon at the top of the window. Beginning with Defining Rational Equations, work through each part of the tutorial. You will be guided through each step of the process. As you work through the mini-example, focus on the following questions:
- How do you multiply the LCD against each side of the equation?
- Why do you end up with a quadratic equation after multiplying each side of the equation by the LCD? Will this happen every time?
Self-Check 1
Complete Solving Rational Equations Self-Check.
1.8. Explore 4
Module 6: Rational Expressions
Factoring to Find the LCD
You have now learned the basics of solving rational equations. You can apply the principles you have learned to other rational equations. In order to identify the lowest common denominator more easily, try factoring the denominators. Keep this in mind as you complete Try This 3.
Try This 3
Study the following rational equation:
![]()
How would you solve this equation? The approach you learned previously can be applied here. Follow the steps in the table to determine the solution.
| Step | Your Work |
| Step 1: Determine the non-permissible values. |
|
| Step 2: Determine the LCD. |
|
Step 3: Multiply by the LCD. |
|
Step 4: Solve for x. |
![]() Save your work in your course folder.
Save your work in your course folder.
Share 2
With a classmate discuss the following questions.
- Compare and contrast the work required to solve
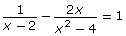 to the work that was required to solve
to the work that was required to solve 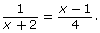
- In the last step, you should have obtained two possible roots. However, did you notice that one of the roots is also a non-permissible value? What does this imply?
![]() Save your work in your course folder. You will refer to your responses later in the lesson.
Save your work in your course folder. You will refer to your responses later in the lesson.
1.9. Explore 5
Module 6: Rational Expressions
Working with Quadratic Denominators
Some rational equations contain denominators that are quadratic expressions. In these cases, a good approach for finding the LCD is to factor the denominators first.
Another good practice in solving rational equations is to check your solution. Do the roots satisfy the original equation? If not, is it because a root is extraneous or is it because an error was made when solving the equation?
Read through “Example 1” on pages 342 to 343 in the textbook. As you read, pay attention to the following points:
- How is the LCD determined?
- How is the equation simplified?
Self-Check 2
- Complete “Your Turn” on page 343 of the textbook. Answer
- Complete “Your Turn” on page 344 of the textbook. Answer
In Share 2 you discovered it is possible to obtain a root of a rational equation that also happens to be a non-permissible value. When this occurs, the root is considered extraneous. If you obtain an extraneous root, it does not necessarily mean that you have done something wrong. In fact, extraneous roots can be obtained even if you do not make any errors.
Turn to “Example 2” on page 344 of the textbook. On this page you will find a rational equation that appears to have two roots. In fact, one of the roots is extraneous. Work through the example and try to find out how it is possible for an extraneous value of the variable to be obtained.
Self-Check 3
Complete “Practice” question 3 and “Apply” question 6 on page 348 of the textbook. Answer
1.10. Connect
Module 6: Rational Expressions
Connect
Solving rational equations is like working your way through an obstacle course. You have to see the pitfalls, think of a plan, and proceed carefully. Solving rational equations is just as much fun but is not nearly as dangerous.

Goodshoot/Thinkstock
Lesson 4 Assignment
Open your copy of Lesson 4 Assignment, which you saved in your course folder at the start of this lesson. Complete the assignment.
![]() Save your work in your course folder.
Save your work in your course folder.
Project Connection
Go to Module 6 Project: Game Challenge. Complete Step 4.
![]() Save your work in your course folder.
Save your work in your course folder.
Going Beyond

iStockphoto/Thinkstock
You have learned that the principles guiding the solutions of rational equations are the same as those for any other type of equation. To solve an equation, you must
- isolate the variable
- balance the equation
In this activity you will explore different types of games, both of which are puzzles that require forward thinking.
Part A: Sliding Puzzles
Have you ever solved a sliding puzzle? The object of these puzzles is to slide the pieces around until each one is in the right place. Launch “Image Shuffle.” Double-click on the image and then try to solve the puzzle by clicking on the puzzle pieces to move them.
You may have seen sliding puzzles that use image fragments instead of numbers. Search the Internet for “sliding puzzle picture.” Are these puzzles more or less difficult? How does your strategy change when dealing with image fragments instead of numbers?
Part B: Perfect Balance
There are many ways to balance an equation. However, some ways are more efficient than others. Search the Internet for “Kongregate Perfect Balance.” Play the interactive game or download the “Perfect Balance” app to test your skills at balancing shapes. Be careful! Each round gets progressively more difficult. Plan ahead so you can achieve the perfect balance!
1.11. Lesson 4 Summary
Module 6: Rational Expressions
Lesson 4 Summary

Comstock/Thinkstock
In this lesson you investigated the following questions:
- What principles are common to the strategies for solving rational equations and how are these principles helpful?
- Why are some values of the variable that are obtained in solving rational equations not roots of the equations?
You discovered that solving rational equations is like solving puzzles. The approach taken should simplify the overall task. In the case of rational equations, clearing the denominators is a good way to simplify the task. By doing so, you are left with either a linear or a quadratic equation to solve. Watch Steps for Solving Rational Equations for a visual of this process.
Extraneous roots occur when the value of the variable obtained is also a non-permissible value. Non-permissible values are unique to rational expressions where a variable occurs in the denominator. However, since the solution process involves solving an equivalent non-rational equation (with no denominators, hence no restrictions), it is possible for an extraneous solution to be obtained.
In the next lesson you will learn how to model problems with rational equations. You will use the strategies you developed in this lesson to solve those problems.