Lesson 1
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-1 SS |
| Book: | Lesson 1 |
| Printed by: | Guest user |
| Date: | Monday, 15 September 2025, 2:39 PM |
Description
Created by IMSreader
1. Lesson 1
Module 7: Absolute Value and Reciprocal Functions
Lesson 1: Absolute Value
Focus
Adele Bloch-Bauer's Portrait by Gustav Klimt.
The image here is a reproduction of a famous painting by Gustav Klimt, who created it in 1907. The painting features the wife of a wealthy businessman and was created out of oil paints and gold. If you had the financial resources, how much would you pay to own this painting?
This painting sold in 2006 for $135 million! Some may say that this is a fair price to pay for a rare and beautiful piece of artwork, while others may see it as grossly overpaying for what amounts to a simple portrait.
Paintings, like other investments, generally increase in value over time. Aspects of the painting such as its composition (oil or acrylic), subject, condition, and rarity all contribute to its market value. In the end, a painting is worth what someone will pay for it. Nevertheless, wouldn’t it be great to be able to determine the absolute value of a painting—the one true value of a piece of artwork that neither shortchanges the seller nor gouges the buyer?
In this lesson you will study the concept of absolute value in the context of mathematics. You will learn how to apply the absolute value of numbers in different situations, including the world of art.
Outcomes
At the end of this lesson you will be able to
- determine the distance of two real numbers of the form ±a, a ∈
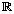, from 0 on a number line, and relate this to the absolute value of a or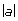 
- determine the absolute value of a positive or negative real number
- explain, using examples, how distance between two points on a number line can be expressed in terms of absolute value
- determine the absolute value of a numerical expression
- compare and order the absolute values of real numbers in a given set
Lesson Questions
In this lesson you will investigate the following questions:
- How can you determine the absolute value of a mathematical expression?
- Under what circumstances is the absolute value of an expression used to solve a problem?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 1 Assignment (Download the Lesson 1 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Module 7 Glossary Terms and Formula Sheet
- work under Project Connection
Self-Check activities are for your own use. You can compare your answers to suggested answers to see if you are on track. If you are having difficulty with concepts or calculations, contact your teacher.
1.1. Launch
Module 7: Absolute Value and Reciprocal Functions
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? This section, which includes Are You Ready? and Refresher, will help you find out.
Before beginning this lesson, you should be able to
- order values on a number line
- use the proper order of operations
1.2. Are You Ready?
Module 7: Absolute Value and Reciprocal Functions
Are You Ready?
Complete these questions. If you experience difficulty and need help, visit Refresher or contact your teacher.
- Consider the following numbers: −3, 0, 2, −2.5,
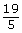
- Evaluate.
How did the questions go? If you feel comfortable with the concepts covered in the questions, skip forward to Discover. If you experienced difficulties, use the resources in Refresher to review these important concepts before continuing through the lesson.
1.3. Refresher
Module 7: Absolute Value and Reciprocal Functions
Refresher
Use Number Line to review the definition and some examples of number lines.
Also practise ordering numbers on the number line using the gizmo “Real Number Line – Activity A.”
Screenshot reprinted with permission of ExploreLearning
Use Order of Operations to review the definition and some examples of number lines.
Also practise ordering numbers on the number line using the gizmo “Order of Operations.”
Screenshot reprinted with permission of ExploreLearning
Go back to the Are You Ready? section, and try the questions again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 7: Absolute Value and Reciprocal Functions
Discover
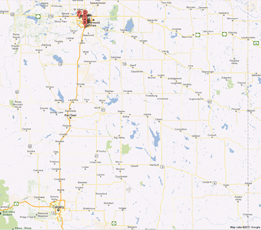
©2011 Google - Imagery ©2011 TerraMetrics, map data ©2011 Google.
What is the distance between Edmonton and Calgary? How does your answer compare to the distance between Calgary and Edmonton? Is there a difference? Would you use negative, positive, or both kinds of values to describe distance? In this Discover section you will consider the answers to these questions by experimenting with an applet.
Try This 1
Part A: Investigating the Absolute Value of a Number
Launch the Absolute Value applet. After clicking to start the applet, you will notice that it has two panels: the left panel has a slider for a and the right one has a number line.
On the number line, click and drag the point marked by x to 0. Check the lower left side of the right panel to make sure that x = 0.0. Note the value of 
and record it in a table like the one shown. This is the absolute value of x. (Both x and a should be at 0 to begin the activity.)
| x |  |
Value |
| 0 | ||
| 2 | ||
| −2 | ||
| 7 | ||
| −7 | ||
| 4.3 | ||
| −0.8 |
- Complete the table by dragging the x on the number line to the other points shown in the table. Record your answers in the appropriate row.
- Based on your observations, how would you instruct someone to determine the absolute value of a number?
Part B: Investigating the Absolute Value of an Expression
In the left panel, drag the appropriate slider so that a = 2
In the right panel, click and drag x to 5. Record the resulting expression for 
(shown in the lower-left corner of the right panel) in a table like the one that follows
| x | a |  |
Value |
| 5 | 2 |  |
|
| −5 | 2 | ||
| −3 | −5 | ||
| 3 | −5 | ||
| −3 | 5 | ||
| 4 | −4 | ||
| −1 | −6 |
- Complete the table by dragging the x on the number line to the other points shown in the table. Record your answers in the appropriate row.
- Based on your observations, how would you instruct someone to determine the absolute value of an expression?
Save your work in your course folder. You will confirm these results later in the lesson.
1.5. Explore
Module 7: Absolute Value and Reciprocal Functions
Explore
Comstock/Thinkstock
Over one 30-day period in Beaumont, the daily high temperature dropped from −1.5°C to −4.3°C, then rose to 9.7°C, and then dropped again to 2.9°C. How would you determine the total change in temperature for the 30-day period? In your calculations, does the order in which you subtract temperatures matter?
In this lesson you will learn how to determine the solution to this question and others like it. You will investigate the absolute value of numbers and numerical expressions.
Save Module 7 Glossary Terms in your course folder now.
Here are some of the words you will want to define in Module 7 Glossary Terms in this lesson:
- absolute value
- absolute value symbol
1.6. Explore 2
Module 7: Absolute Value and Reciprocal Functions
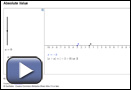
Number Line
Any real number can be found on the real number line. The absolute value of a number is its distance from zero on the number line.
Try This 2
Answer the following questions based on the definition of absolute value.
- How far is the number 3 from zero on the number line?
The absolute value of 3 is _____________ .
- How far is the number −3 from zero on the number line?
The absolute value of −3 is _____________ .
- How far is the number a from zero on the number line?
The absolute value of a is _____________ .
- How far is the number −a from zero on the number line?
The absolute value of −a is _____________ .
Save your responses in your course folder.
1.7. Explore 3
Module 7: Absolute Value and Reciprocal Functions
Vertical bars are used to indicate the absolute value of a number or expression. The vertical bars are known as the absolute value symbol. The following table shows how you can use the absolute value symbol to represent the numbers in Try This 2.
| Description | Representation |
| absolute value of 3 |  |
| absolute value of −3 |  |
| absolute value of a |  |
| absolute value of −a |  |
You can also evaluate the absolute value of an expression.
A good strategy when simplifying absolute value expressions is to first evaluate the expression inside the absolute value symbol.
Try This 3
- Evaluate the following expressions. For each one, record any strategies you may have used to determine the answer.
Expression Simplification Strategies/Notes a.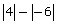 
b.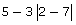 
c.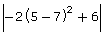 
- Turn to “Example 3” on page 361 of your textbook. The questions in this example are the same as those in the table for question 1. Compare your answers to those in the textbook. If there are any discrepancies, note them, and then make any necessary revisions to your own work.
Save your responses in your course folder.
1.8. Explore 4
Module 7: Absolute Value and Reciprocal Functions
Self-Check 1
- For each of the statements a. to e., indicate which of the following answers (A, B, or C) applies.
- −7
- 7
- neither
- Evaluate the following expression and indicate which answer applies.
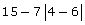
- −16
- 1
- 16
- 29
Answer
- Evaluate the following expression and indicate which answer applies.
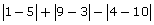
- 4
- 8
- −8
- −4
Answer
- Evaluate the following expression and indicate which answer applies.
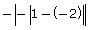
- −3
- −1
- 1
- 3
Answer
Absolute Value and Distance
In the introduction to the lesson you were asked to compare the distance from Edmonton to Calgary, and from Calgary to Edmonton. In fact, the distances are the same and, in both cases, reported as positive numbers. The concept of absolute value is useful in determining distances between numbers on a number line, where the answer is always positive. Study the next example to see two ways to use absolute value to represent the distance between two numbers on the number line.
Example
Determine the distance between the numbers 5 and −1.2 on the number line.
Solution
Method 1: Subtract the smaller number from the larger number.
Method 2: Calculate the absolute value of the difference of the two numbers.
| Alternative A | Alternative B |
 |
 |
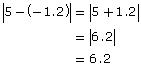Share 1
With a partner, discuss the following questions based on the example. Record your answers and save them in your course folder.
- What are the advantages and one disadvantage of each method?
- In Method 2, why is it not necessary to identify the larger of the two numbers?
Save your responses in your course folder.
1.9. Explore 5
Module 7: Absolute Value and Reciprocal Functions
Ordering Absolute Values
Now that you know how to determine the absolute value of numbers and numerical expressions, you can compare and order several absolute value expressions in a set.
Turn to “Example 2” on page 361. This example shows you how to order absolute value expressions. Work through the example carefully. Pay attention to the steps that are presented. Would you approach this task differently? If so, explain how.
Self-Check 2
Answer the questions in the piece titled Ordering Absolute Value Expressions Self-Check.
© Ilyes Laszlo/5882188/Fotolia
In certain cases, you may be interested in knowing the total change of a particular variable such as distance, investment, or temperature. In the last section of this lesson, you will encounter some scenarios that can be solved by using absolute values.
Try This 4
Recall the situation presented in the introduction to the Explore section.
Over one 30-day period in Beaumont, the daily high temperature dropped from −1.5°C to −4.3°C, then rose to 9.7°C, and then dropped again to 2.9°C.
Determine the total change in temperature for the 30-day period by following these steps.
- Generate an absolute value expression for each change in temperature.
- Determine the sum of the expressions generated in question 1.
Save your responses in your course folder.
Share 2
With a partner, discuss the following questions relating to Try This 4.
- Does the order in which you subtract the temperatures in step 1 matter? Why or why not?
- Determine the difference between the temperature at the beginning of the 30-day period and the temperature at the end of the 30-day period. How is this value different from your answer to question 2 in Try This 4?
Save your answers in your course folder.
1.10. Explore 6
Module 7: Absolute Value and Reciprocal Functions
Turn to “Example 4” on page 362 to find a situation that is similar to the one described in Try This 4. Work through the example and focus on the answers to the following question:
- How can information about the total change in stock value help an investor make decisions about his or her investments?
Self-Check 3
Turn to pages 364–367 of your textbook to practise applying the concepts that you have learned. Complete questions 9, 11, and 23. Check the solutions in the back of the textbook to make sure you are doing the questions correctly. You may also want to review relevant parts of the lesson as you work through the questions.
1.11. Connect
Module 7: Absolute Value and Reciprocal Functions
In the Lesson 1 Assignment you will demonstrate your understanding of the lesson outcomes. You will apply the concepts and strategies you learned to new situations. You must show your work to support your answers.
Open your copy of Lesson 1 Assignment, which you saved in your course folder at the beginning of this lesson. Complete the assignment.
Save all your work in your course folder.
Project Connection
In this lesson you learned how to interpret, evaluate, and order absolute value expressions. You are now ready to move on to the project. Go to the project now and complete Step 1.
Save all your work in your course folder.
Going Beyond
© Kamaga/2832245 /Fotolia
What does the term absolute mean?
How is the word absolute used in other fields such as science, law, and politics? The following is a list of expressions that contain the word absolute. What similarities, if any, do the definitions of the following expressions have with the definition of absolute value?
| absolute monarchy | absolutism |
| absolute zero | absolute pressure |
| absolute dating | absolute extrema |
| absolute threshold | absolute refractory period |
Save your answers in your course folder.
1.12. Lesson 1 Summary
Module 7: Absolute Value and Reciprocal Functions
Lesson 1 Summary
In this lesson you investigated the following questions:
- How can you determine the absolute value of a mathematical expression?
- Under what circumstances is the absolute value of an expression used to solve a problem?
van Gogh, Vincent. Irises, oil on canvas, 1889. (J. Paul Getty Museum, Los Angeles).
The absolute value of a real number can be thought of as the magnitude or value of the number with no regard to its sign. In this lesson you learned to evaluate absolute value expressions. You determined the absolute value of real numbers by identifying their distance from zero on a number line. You also determined the absolute value of an expression by simplifying expressions and then considering the magnitude of the result.
You learned that the concept of absolute value can be used to determine distances, where negative values have no meaning. You also learned to use absolute values to solve problems related to temperature differences and stock values. In these cases, absolute value is used when negative differences are not wanted.
What do you think the graph of the absolute values of a set of integers looks like? You will find out in the next lesson as you study absolute value functions.