Lesson 3
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-1 SS |
| Book: | Lesson 3 |
| Printed by: | Guest user |
| Date: | Thursday, 4 December 2025, 2:08 AM |
Description
Created by IMSreader
1. Lesson 3
Module 7: Absolute Value and Reciprocal Functions
Lesson 3: Absolute Value Equations
Focus
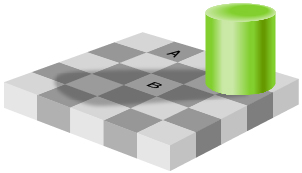
In the illustration, notice that the green cylinder casts a shadow on the checkerboard. Study the colours of the squares marked A and B. They appear to be different shades of grey, but are they? Use a screen capture tool to capture each square. Place them side by side and compare. What do you notice?
The illustration is an example of an optical illusion. Creating an optical illusion takes skill. Your creation needs to appear to reveal one thing, but in fact, it reveals something else. The observer must differentiate between what is real and what is extraneous to have a true sense of what he or she is seeing.
In this lesson you will study absolute value equations. Like optical illusions, you will find that you may generate solutions that appear to be mathematically correct, but are in fact extraneous. You will learn both graphical and algebraic strategies for determining the solutions of absolute value equations.
Outcomes
At the end of this lesson you will be able to
- solve, graphically, an absolute value equation with or without technology
- solve, algebraically, an equation with a single absolute value, and verify the solution
- explain why the absolute value equation
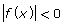 has no solution
has no solution
- determine and correct errors in a solution to an absolute value equation
- solve a problem that involves an absolute value function
Lesson Questions
In this lesson you will investigate the following questions:
- How can the roots of absolute value equations be determined?
- Why are extraneous roots obtained sometimes when absolute value equations are solved algebraically?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 3 Assignment (Download the Lesson 3 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Module 7 Glossary Terms and Formula Sheet
- work under Project Connection
Materials and Equipment
You will need a graphing calculator and graph paper.
1.1. Launch
Module 7: Absolute Value and Reciprocal Functions
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? This section, which includes Are You Ready? and Refresher, will help you find out.
Before beginning this lesson, you should be able to
- work with absolute values
- solve and verify first-degree, single-variable equations
- solve a linear-quadratic system
1.2. Are You Ready?
Module 7: Absolute Value and Reciprocal Functions
Are You Ready?
Complete these questions. If you experience difficulty and need help, visit Refresher or contact your teacher.
-
Define absolute value. Answer
-
If the absolute value of a number is equal to 11, then what could the number be? Answer
- Solve and verify the following equations.
- Solve the following equations graphically, with or without technology. Round solutions to the nearest tenth.
How did the questions go? If you feel comfortable with the concepts covered in the questions, skip forward to Discover. If you experienced difficulties, use the resources in Refresher to review these important concepts before continuing through the lesson.
1.3. Refresher
Module 7: Absolute Value and Reciprocal Functions
Refresher
Use “Absolute Value Equation Example 2” to work with absolute value expressions.
Open “Solving Two-Step Equations” to solve and verify first-degree, single variable equations of various forms.
Use “Non-Linear Systems of Equations 1” to review how to solve a linear-quadratic system.
Go back to the Are You Ready? section, and try the questions again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 7: Absolute Value and Reciprocal Functions
Discover

Are the circles in the illustration different colours, or are they the same colour?
In this section you will investigate the solutions of absolute value equations.
Try This 1
Part A
Consider the equation ![]() = 6.
= 6.
- Is the root of the equation x + 1 = 6 also a root of the equation
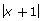 = 6?
= 6?
- Think of another value of x that satisfies the equation
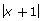 = 6.
= 6.
- Solve
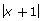 = 6 by graphing with or without technology.
= 6 by graphing with or without technology. 
- Does the solution match your answers from questions 1 and 2?
Part B
Consider the equation ![]() = 2x.
= 2x.
- Is the root of the equation x − 6 = 2x also a root of the equation
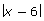 = 2x?
= 2x?
- Solve this equation by graphing with or without technology.

- How can you obtain the solution from question 6 using an algebraic approach?
![]() Save your answers in your course folder.
Save your answers in your course folder.
Share 1
With a classmate, discuss the following questions. Record your responses.
- What are the differences when solving absolute value equations graphically and algebraically?
- How would you instruct someone to solve an absolute value equation algebraically? What tips would you give?
- Why do you think algebraic solutions sometimes lead to extraneous solutions?
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.5. Explore
Module 7: Absolute Value and Reciprocal Functions
Explore

Dmytro Bezsmertnyy, www.hidden-3d.com
A stereogram is an image on a flat surface that renders an illusion of three dimensions. The 3-D image hidden within a stereogram typically cannot be seen with a casual glance. In order to view the image, you must apply any of several methods that “trick” your eyes into seeing the image or, more likely, allow your eyes to focus properly. For example, people have had success by focusing beyond the image, or even crossing their eyes. By disregarding the extraneous and focusing one’s attention on the middle of the image, you will be able to see what was previously unseen. Print Stereogram, and then try the suggested techniques to see if you can spot the two creatures hiding in the “grass.”
In this lesson you will learn to identify extraneous solutions when solving absolute value equations, much like you would ignore the extraneous details when working with stereograms.
Here is one of the words you will want to define in Module 7 Glossary Terms in this lesson:
- absolute value equation
1.6. Explore 2
Module 7: Absolute Value and Reciprocal Functions
Solving Absolute Value Equations Graphically
You have solved many different types of equations by graphing. In Discover you saw how you can also solve absolute value equations by graphing.
Generally, there are two approaches when solving by graphing. The following methods can be applied with or without technology.
Method 1: Intersect Method
Step 1: Graph the function represented by the left-hand side of the equation.
Step 2: Graph the function represented by the right-hand side of the equation.
Step 3: Determine the point(s) of intersection between the two functions to reveal the solution(s).
Method 2: Zero Method
Step 1: Graph the function represented by the side of the equation containing all of the terms.
Step 2: Determine the zero(s) of the function to reveal the solution(s).
Launch the “Absolute Value Equations” applet to see how you can use a table to solve an absolute value equation graphically. Click on the blackboard at the top of the screen to see the tutorials. Choose “Sovling: Graphically.”
Self-Check 1
Turn to page 389 of your textbook to practise solving absolute value equations by graphing. Use a graphical method of your choice to solve the equations found in questions 2 and 4. Answer
1.7. Explore 3
Module 7: Absolute Value and Reciprocal Functions
Solving Absolute Value Equations Algebraically
Recall the piecewise definition of an absolute value expression ![]() :
:
![]()
This notation implies that there are two cases to consider when evaluating an absolute value expression depending on the sign of the expression contained by the absolute value symbol.
Similarly, you need to be aware that there may be more than one possible solution when solving an absolute value equation.
Consider the equation ![]() . Recall that the definition of an absolute value number is the number’s distance from zero on a number line. Since
. Recall that the definition of an absolute value number is the number’s distance from zero on a number line. Since ![]() and
and ![]() , the roots of the equation are 6 and −6.
, the roots of the equation are 6 and −6.
![]()
Recall the activity in the Discover section. In that exercise you solved the equation ![]() . You can approach this equation in the same way as solving
. You can approach this equation in the same way as solving ![]() . Work through the “Absolute Value Equations” applet to see how this is done. Select the Tutorial icon, and then select “Solving: Algebraically.”
. Work through the “Absolute Value Equations” applet to see how this is done. Select the Tutorial icon, and then select “Solving: Algebraically.”
Self-Check 2
Use a personal strategy to solve the following absolute value equations.
1.8. Explore 4
Module 7: Absolute Value and Reciprocal Functions
Absolute Value Equations with Extraneous Solutions
Retrieve your results from Part B of Try This 1, which you completed in the Discover section.
In that exercise, you solved the equation ![]() both graphically and algebraically.
both graphically and algebraically.
Study the next example carefully to see if your results match the solution shown.
Example
Solve the equation ![]() .
.
- graphically
- algebraically
Solution
- You can use the same graphical approach as the one you used before.
Enter Y1 =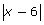 .
.
Enter Y2 = 2x.
You can set your window as x = [−5, 20, 5], y = [−2, 20, 5].
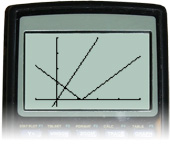
There appears to be only one solution at x = 2. It is not expected that the graphs will intersect again.
-
You can use the same algebraic approach as the one you used before.
Case 1: x − 6 > 0
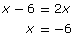
Case 2: x − 6 < 0
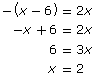
It appears that there are two solutions to this equation. However, the graphical solution only revealed one root. There may be an extraneous root.
Share 2
Complete the tasks and answer the following questions together with a classmate.
- Verify the roots obtained from the algebraic approach to the previous example.
- Which root is extraneous and why?
- What other ways could you identify a root as extraneous?
![]() Record and save your answers in your course folder.
Record and save your answers in your course folder.
1.9. Explore 5
Module 7: Absolute Value and Reciprocal Functions
The extraneous root in the previous example was x = −6. You may have verified this by substituting x = −6 into the original equation, as shown below.

Another way that you may have confirmed that x = −6 is extraneous is to consider the domain of the function. The expression ![]() can be expressed using piecewise notation as
can be expressed using piecewise notation as
![]()
In Case 1, where x − 6 > 0, since x = −6 is not in the domain of x ≥ 6, this solution is an extraneous one.
In Case 2, where x − 6 < 0, since x = 2 was in the domain x < 6, this solution is valid.
In the future you may wish to substitute values into the original equation to verify their validity. Alternatively, you may wish to compare obtained solutions to the appropriate domain to check for extraneous solutions.
Self-Check 3
Turn to page 389 of your textbook to practise solving absolute value equations by graphing. Use a graphical method of your choice to solve the equations found in questions 5.b. and d., and 6.a., c., and e.
1.10. Explore 6
Module 7: Absolute Value and Reciprocal Functions
Solving Problems Involving Absolute Value Equations
Absolute value equations can be used to model and solve problems dealing with the concept of tolerances. Tolerance is the amount of variation allowed in the measure of a quantity. Work through the next Try This activity to see an example.
Try This 2

© diter/4749715 /Fotolia
A ballistic vest is used to protect a person from injury by bullets. Typically worn by police officers in potentially hostile territory, these vests are subjected to strict testing to ensure safety and quality. In most cases, the performance of a ballistic vest is judged to be greater as it is able to withstand bullets fired at higher velocities. For example, a Type II vest protects against 9-mm bullets travelling at a speed of 398 m/s ± 9 m/s.
- Write an absolute value equation that can be used to determine the greatest and least velocities allowed.

- Solve the equation. What is the greatest velocity allowed? What is the least velocity allowed?
- With what other methods could you solve this problem?
Turn to “Example 2” on pages 383–384 to see how a different, but related, problem can be solved by an absolute value equation. As you read, focus on the two methods that are presented. How do you know if the solutions are reasonable?
Share 3
A good way to check your understanding of the concepts presented in this lesson is to analyze the work of another student. With a partner, turn to the following questions in your textbook. Discuss any errors in the solution. Copy the equation and show the correct work with the correct solution.
- Go to page 390 and answer question 15.
- Go to page 413 and answer question 9.
![]() Record your answers in your course folder.
Record your answers in your course folder.
Self-Check 4
Turn to pages 389–391 of your textbook to practise applying the concepts that you have learned. Complete questions 9, 11, and 23. Check the solutions in the back of the textbook to make sure you are doing the questions correctly. You may also want to review relevant parts of the lesson as you work through the questions. Answer
1.11. Connect
Module 7: Absolute Value and Reciprocal Functions
Open your copy of Lesson 3 Assignment, which you saved in your course folder at the beginning of this lesson. Complete the assignment.
![]() Save all your work in your course folder.
Save all your work in your course folder.
Project Connection
In this lesson you learned how to use both graphical and algebraic methods to solve absolute value equations. You are now ready to move on to the next phase of your project. Go to your project now and complete Step 3.
![]() Save all your work in your course folder.
Save all your work in your course folder.
Going Beyond

© Delphimages/21883219 /Fotolia
There are two ways that you can extend beyond this lesson.
Part A: Solving Equations with Two Absolute Values
Open “Absolute Value Equations.” Then click on the puzzle piece icon at the top of the page, and work through “Equations with Two Absolute Values I” and “Equations with Two Absolute Values II.”
Part B: Analyzing Stereograms
In this lesson you learned about stereograms. There are some websites that allow you to create your own stereogram. Do an Internet search using the keywords “stereogram generator” to see how easily this can be done. Experiment with different words and patterns. Use a screen capture tool to copy your finished stereogram to your course folder.
1.12. Lesson 3 Summary
Module 7: Absolute Value and Reciprocal Functions
Lesson 3 Summary

Dmytro Bezsmertnyy, www.hidden-3d.com
In this lesson you investigated the following questions:
- How can the roots of absolute value equations be determined?
- Why are extraneous roots obtained sometimes when absolute value equations are solved algebraically?
In this lesson you learned graphical and algebraic strategies for solving absolute value equations. Since absolute value expressions are dependent on the sign of the expression contained in the absolute value symbol, there are two cases to consider when solving absolute value equations algebraically.
For the equation ![]() , where A is a mathematical expression, you must determine the solutions to the following two cases:
, where A is a mathematical expression, you must determine the solutions to the following two cases:
- Case 1: f(x) = A
- Case 2: −f(x) = A
You also learned that the algebraic method may yield extraneous roots. It is necessary, therefore, to verify that the roots either satisfy the specific domain or result in a true statement when substituted back into the original equation. Extraneous roots are obtained because the domain of each case is restricted to positive or negative values of x, but values outside of the domain emerge when solving quadratic and linear equations.
In the final lesson of this module you will explore reciprocal functions. These and absolute value functions may be used to develop further math concepts in subsequent math courses.