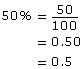Section 1
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-3 SS |
| Book: | Section 1 |
| Printed by: | Guest user |
| Date: | Tuesday, 2 December 2025, 6:58 AM |
Description
Created by IMSreader
Table of contents
- 1. Section 1
- 1.1. Lesson 1
- 1.2. Launch
- 1.3. Are You Ready?
- 1.4. Refresher
- 1.5. Discover
- 1.6. Explore
- 1.7. Explore 2
- 1.8. Explore 3
- 1.9. Connect
- 1.10. Lesson 1 Summary
- 1.11. Lesson 2
- 1.12. Launch
- 1.13. Are You Ready?
- 1.14. Refresher
- 1.15. Discover
- 1.16. Explore
- 1.17. Explore 2
- 1.18. Explore 3
- 1.19. Explore 4
- 1.20. Connect
- 1.21. Lesson 2 Summary
- 1.22. Lesson 3
- 1.23. Launch
- 1.24. Are You Ready?
- 1.25. Refresher
- 1.26. Discover
- 1.27. Explore
- 1.28. Explore 2
- 1.29. Explore 3
- 1.30. Connect
- 1.31. Lesson 3 Summary
- 1.32. Lesson 4
- 1.33. Launch
- 1.34. Are You Ready?
- 1.35. Refresher
- 1.36. Discover
- 1.37. Explore
- 1.38. Explore 2
- 1.39. Explore 3
- 1.40. Connect
- 1.41. Lesson 4 Summary
- 1.42. Section 1 Project
- 1.43. Section 1 Summary
1. Section 1
Section 1: Simple and Compound Interest

iStockphoto/Thinkstock
Section 1 Introduction
How are your financial gardening skills? Are you interested in seeing your money grow? Don’t let your money sit neglected and withering on the vine. Invest! Banks, credit unions, governments, and businesses will all pay you when you deposit cash with them. They’ll pay you interest!
In the Section 1 Project: Capturing Your Interest!, you will explore various investments that earn interest. While working through the lessons, you will investigate how to make simple interest and compound interest work. You will discover how each type of interest is calculated and look at similarities and differences. Then, armed with this knowledge, you too can plant the seed for your financial money tree.
1.1. Lesson 1
Section 1: Simple and Compound Interest
Lesson 1: Simple Interest
Focus

Hemera/Thinkstock
You may have heard the old saying “Money doesn’t grow on trees!” But your money can grow! When you put your hard-earned money into a savings account, buy a guaranteed investment certificate (GIC), or invest in regular-interest savings bonds, you earn interest. This is true since a bank, a business, or a government is effectively renting your money for their use.
The reverse is also true—a bank or business will charge you interest if they loan you money to make a purchase or pay a bill.
In this lesson you will examine one form of interest called simple interest. This is interest calculated on an amount of money that does not include interest earned.
Lesson Question
In this lesson you will investigate the following question:
- How can you solve financial problems involving simple interest?
Assessment
Your assessment for this lesson may include a combination of the following:
- course folder submissions from the Try This and Share sections of the lesson
- your contribution to the Mathematics 20-3 Glossary Terms and the Formula Sheet
- Lesson 1 Assignment (Save a copy of your lesson assignment to your course folder now.)
- the Project Connection
In this course you may come across Self-Check questions, Try This questions, and other activities that may or may not be assessed.
Remember that these questions and activities provide you with the practice and feedback that you need to successfully complete this course. You should respond to all the questions and place those answers in your course folder. Your teacher may wish to view the work that you have stored in your course folder to check on your progress and to see if you require assistance.
Materials and Equipment
- calculator
Time
This lesson has been designed to take 150 minutes; however, it may take more or less time depending on how well you are able to understand the lesson concepts. It is important that you progress at your own pace based on your learning needs.
1.2. Launch
Section 1: Simple and Compound Interest
Launch
This section checks to see if you have the necessary background knowledge and skills required to successfully complete Lesson 1.
Complete the following Are You Ready? questions. If you have difficulty or any questions, visit Refresher for a review or contact your teacher.
An important skill in solving simple interest problems is working with percentage; specifically converting back and forth between percentage and decimals.
1.3. Are You Ready?
Section 1: Simple and Compound Interest
Are You Ready?
- Convert each percentage to a decimal numeral.
- 50%
- 4.5%
- 0.4%
- Convert each decimal to a percentage.
- 0.25
- 3.2
- 0.001
- Calculate 16% of 72. Answer
If you answered the Are You Ready? questions without problems, move on to Discover.
If you found the Are You Ready? questions difficult, complete Refresher to review these topics.
1.4. Refresher
Section 1: Simple and Compound Interest
Refresher
If you don’t know the answers for Are You Ready?, or require more information, study the following information about percentages.
This data clarifies why changing a percent to a decimal numeral means moving the decimal in the percent two places to the left.
The following clarifies why changing a decimal to a percent means moving the decimal point two places to the right.
- Use proportional reasoning. Let the required percentage be n%.
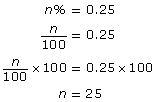
So, 0.25 = 25%
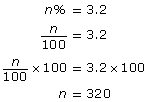
So, 3.2 = 320%
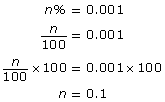
So, 0.001=0.1%
Go back to Are You Ready? and try the questions again. Contact your teacher if you continue to have difficulty.
1.5. Discover
Section 1: Simple and Compound Interest
Discover
In this section you will derive the formula to find simple interest.
Try This 1
Use the Simple Interest Calculator to help investigate how simple interest is calculated. Click on the play button.
PART 1: Manipulating the Interest Rate (r)
- Using the Simple Interest Calculator, what is the interest earned on $100 for one year at
- 4%
- 10%
- Without using the calculator, can you predict how much simple interest you will earn when you invest $100 for one year at an interest rate of 20%? Check your answer using your calculator.
- How do you think the Simple Interest Calculator calculated the values for questions 1 and 2?
PART 2: Manipulating the Time (t)
- Using the Simple Interest Calculator, what is the interest earned on $100 at an interest rate of 5% for
- 1 year
- 2 years
- Without using the calculator, can you predict how much simple interest you will earn when you invest $100 for 10 years at an interest rate of 5%? Check your answer using your calculator.
- How do you think the Simple Interest Calculator calculated the values for questions 1 and 2?
PART 3: Putting It All Together
- Based on your observations from Parts 1 and 2, suggest a formula for finding interest. Use the following symbols to build your formula.
- I for interest
- P for principal
- r for the annual interest rate
- t for the time in years
![]() Save your answers to your course folder.
Save your answers to your course folder.
Share 1
As you are working on this Share section, refer to the Share Rubric. This information will help you understand what your teacher expects of you.
Share your responses to the Part 3 question from Try This 1 with a classmate or group.
- How did your formula for finding interest compare with other students’ formulas? Why might there have been similarities and differences between the formulas?
- Use your formulas to find what the total interest on $6000 at 5% would be after ten years. Use the Simple Interest Calculator to check if your formulas are correct.
If required, save a copy of your discussion and calculation in your course folder.
1.6. Explore
Section 1: Simple and Compound Interest
Explore
Did You Know?
Charging interest on loans has been around for thousands of years. The ancient Babylonians and Romans limited the amount of interest charged. Rates were limited to between 25% and 50% for loans of grain or precious metals.
At about 1000 CE in Indochina, loans of rice were charged interest of 50% payable at the time of the next harvest.

Digital Vision/Thinkstock
In Discover you may have noticed that simple interest calculations depend on three factors:
- The first factor is the amount borrowed or invested. This amount is called the principal.
- A second factor determining interest is the interest rate. Banks advertise the interest rate as an annual rate—the rate charged or earned for one year.
- A third factor is the term or time, expressed in years, of the loan or investment.
In Discover you used these factors to help develop a formula for simple interest. The formula may have looked similar to the following one. Roll-over the formula to identify the variables.
I = Prt ![]()
Watch Marty’s Notebook to see how the simple interest formula can be used. Access this applet by clicking on the play button. Notice the extra step required when the time given is in months.
To find the total amount of money an investment is worth, the principal and all the interest made must be added together.
![]()
You may have noticed that this formula was used in the final step in the example you just watched. You will see this formula used again at the end of question 1 of Self-Check 1.
P = the principal or original amount invested
r = annual interest rate in decimal form
t = the term, or time in years
1.7. Explore 2
Section 1: Simple and Compound Interest

Amos Morgan/Photodisc/Thinkstock
Self-Check 1
- Jolene Danchuk has just invested $1000 in a 90-day GIC at her bank. The GIC earns simple interest at 3% per annum. How much will Jolene’s investment be worth after 90 days? Answer
- Do question 1 from “Build Your Skills” on page 272 of MathWorks 11. Answer
- Do question 3 from “Build Your Skills” on page 273 of MathWorks 11. Answer
In Example you will see that you can find any of the variables in the simple interest formula as long as only one variable is missing.
In the example about Morris, you found the interest rate using the formula when you knew the interest earned, the principal, and the loan’s term.
In the formula I = Prt, you knew I, P, and t, and you had to find r.
Anytime you are given three of the four values in the formula, you can determine the fourth.
In the example, you substituted directly into the formula I = Prt. You could rearrange the formula first if you prefer. If you want to determine r, you can rearrange the formula as follows.
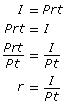
In Self-Check 2, try rearranging the formula before substituting into the simple interest formula.
1.8. Explore 3
Section 1: Simple and Compound Interest
Self-Check 2
- Suu Kyi invested $4000 in a five-year regular interest bond. She will receive $200 in simple interest over the five-year term. What is the annual interest rate on the bond? Use the rearranged formula,
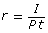 . Answer
. Answer
- Do question 2 from “Build Your Skills” on pages 272 and 273 of MathWorks 11. Answer
It is now time to add new math terms, defintions, and examples/notes to your Mathematics 20-3: Glossary Terms document. Complete the missing pieces of the document, and save it to your desktop. Note that some terms, defintions, and examples/notes have already been provided in the document.
In this lesson the new terms you will add are
- principal (P)
- interest rate (r)
- term (t)
- simple interest (I)
- annum
- total amount (accumulated amount is the same thing)
At this time you may want to add the two formulas used in this lesson to your Formula Sheet.
Throughout Mathematics 20-3 you will encounter formulas that you will use to solve problems. It is useful to keep track of the formulas as you move through the lessons.
Save Formula Sheet in your course folder now. You will update this document throughout Module 2.
1.9. Connect
Section 1: Simple and Compound Interest
Connect
Going Beyond
For short-term investments or loans for which the term is given in days, 360 days are used instead of 365 days to mentally estimate the interest.
For instance, estimate the simple interest on a 60-day GIC. The principal is $3000, and the interest rate is 2% per annum.
P = $3000
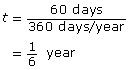
r = 2% = 0.02
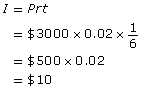
The interest is about $10.
- Use 360 days in a year to approximate what fraction of a year is included for each term.
- 90 days
- 45 days
- 30 days
- Calculate the difference between an estimate and the actual simple interest on a 90-day GIC if $4000 is invested and the interest rate is 2.5%.
Project Connection
The project for this section involves investigating interest on investments and loans.
![]() Begin working on Steps 1 and 2 of the Section 1 Project: Capturing Your Interest! Make sure to save all your project work in your course folder to submit at the end of Section 1.
Begin working on Steps 1 and 2 of the Section 1 Project: Capturing Your Interest! Make sure to save all your project work in your course folder to submit at the end of Section 1.
Lesson 1 Assignment
Your lesson assignment contains some problems for you to solve using knowledge gained during the lesson. Now you will have the chance to apply the concepts and strategies that you have learned to a new situation. Show work to support the answers.
Open the Lesson 1 Assignment that you saved to your course folder and complete the questions.
1.10. Lesson 1 Summary
Section 1: Simple and Compound Interest
Lesson 1 Summary

Hemera/Thinkstock
In this lesson you examined simple interest on loans and investments. To solve simple interest problems, you discovered that you had to know three of the four quantities: interest, annual interest rate, principal, and the term in years.
Interest on loans and investments has been part of human civilization for thousands of years. In ancient Babylon, regulations governed the interest lenders could legally charge. The same is true today in Canada. All charges and interest must be disclosed to the borrower, so that the borrower knows from the beginning how much interest the loan will cost. Remember to read the fine print before signing on the dotted line! And keep in mind that only legitimate borrowing is dealt with in this lesson.
1.11. Lesson 2
Section 1: Simple and Compound Interest
Lesson 2: Compound Interest
Focus

Wendy Hope/Stockbyte/Thinkstock
Training for physical endurance in a race is a long-term process. Saving money through investing is also a long-term process. Most people do not become rich overnight. When training for a race, an athlete will focus on increasing strength and power. Similarly, using interest to increase your savings is using the power of interest.
In Lesson 1 you looked at the power of simple interest. In this lesson you will look at an even bigger powerhouse: compound interest.
Lesson Question
In this lesson you will investigate the following question:
- How are financial problems involving compound interest solved?
Assessment
Your assessment for this lesson may include a combination of the following:
- course folder submissions from the Try This and Share sections of the lesson
- your contribution to the Mathematics 20-3 Glossary Terms and the Formula Sheet
- Lesson 2 Assignment (Save a copy of your lesson assignment to your course folder now.)
- the Project Connection
Materials and Equipment
- calculator
1.12. Launch
Section 1: Simple and Compound Interest
Launch
This section checks to see if you have the necessary background knowledge and skills required to successfully complete Lesson 2.
Complete the following Are You Ready? questions. If you have difficulty or any questions, visit Refresher for a review or contact your teacher.
An important skill in solving compound interest problems is working with exponents.
1.13. Are You Ready?
Section 1: Simple and Compound Interest
Are You Ready?
- What is the value of 43? Without using your calculator, explain how you found the answer. Answer
- Use your calculator to evaluate the power (1.04)4. Answer
- What keystrokes did you use in question 2 to find your answer? Answer
-
Evaluate.
If you answered the Are You Ready? questions without problems, move on to Discover.
If you found the Are You Ready? questions difficult, complete Refresher to review these topics.
1.15. Discover
Section 1: Simple and Compound Interest

iStockphoto/Thinkstock
Discover
Try This 1
Jeremy and Sara both receive a graduation gift of $1000. Instead of spending this money, they decide to invest the cash. But both Jeremy and Sara are unsure about investing the money with simple or with compound interest.
Click on the play button in the Simple Interest Versus Compound Interest applet to explore the difference between simple interest and compound interest. Pay close attention to what is happening to the interest after each compounding period.
- In Year 1, both investments earn interest. What is the difference between what happens with this interest between the simple interest investment and the compound interest investment?
- After 15 yr, who earns more money?
![]() Save your answers to your course folder.
Save your answers to your course folder.
Share 1
With a partner or in a group, compare your answers to Try This 1. Discuss the following question:
- Why did one investment earn more than the other investment?
1.16. Explore
Section 1: Simple and Compound Interest
Explore
In Discover you may have noticed the following differences between simple interest and compound interest.
| Simple Interest | Compound Interest |
|
|
|
|
|
|
Did You Know?
Richard Witt’s Arithmeticall Questions, published in 1613, was one of the first books in the English language that contained detailed tables and formulas for calculating both simple and compound interest. You will be using Witt’s formula for compound interest later in this lesson. To apply this formula, you will need your exponent skills! The following illustration is a question on compound interest from Witt’s book.

In Try This 1, both investments are calculated annually—for simple interest this is always the case, so time must be converted to years. However, compound interest may be paid out more than once a year, even though the interest is quoted as annual interest. These shorter periods of time where interest is paid out are called compounding periods.
Due to compounding periods, the compound interest formula is a bit more complicated than simple interest.
![]()
- A is the final amount of the investment.
- P is the principal.
- r is the annual interest rate.
- n is the number of compounding periods in a year.
- t is the term in years.

iStockphoto/Thinkstock
Example
Ravia lives in Fort Vermilion, Alberta. She has just invested $1000 in a five-year, compound interest bond. The annual interest rate is 6%, compounded annually. Use the compound interest formula to see how much her investment will be worth in five years.
Solution
| Identify the variables from the question. | P = $5000 r = 6% = 0.06 t = 5 n = 1 |
| Substitute the known variables into the compound interest formula to find the final amount of the investment (A). | 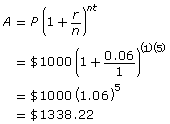 |
1.17. Explore 2
Section 1: Simple and Compound Interest
Self-Check 1

Digital Vision/Thinkstock
Julian downloads a compound interest calculator from the Internet to explore investment possibilities. He has $3000 to invest. At his bank, Julian can earn 3.6% compounded quarterly. How much will Julian have earned in interest if he leaves the money in this investment for 12 years?
The following variables have been identified from the problem. Use the compound interest formula to find the final amount of the investment (A).
P = $3000
r = 3.6% or 0.036 (This is the annual rate.)
n = 4 since the interest is added quarterly (4 times per year)
t = 12 years
In Self-Check 1, the annual interest of 3.6% was compounded quarterly—four times in one year. This means that the annual interest rate was split up over the four compounding periods during the year. The interest rate for each compounding period can be calculated according to the following chart.
| Interest | Number of Compounding Periods Per Year |
Interest Rate Per Compounding Period |
| Annually | 1 (once a year) | Annual Interest Rate |
| Semi-annually | 2 (every 6 months) | |
| Quarterly | 4 (every 3 months) | |
| Monthly | 12 |
The compounding period interest rate for Julian’s investment was the following:

1.18. Explore 3
Section 1: Simple and Compound Interest
Consider Ravia’s investment again. Ravia asked her bank to see what the final investment would have been if the interest were compounded with different compounding periods.
Try This 2
Use the Compound Interest Formula applet to investigate the effects on changing the compounding periods on Ravia’s investment. As you work through the applet, fill in the chart provided in question 1.
- Fill in the chart using the information from Ravia’s $1000 investment.
Compounding Period Number of Compounding Periods Total Amount Interest Earned Annually Semi-annually Quarterly Monthly
- Explain why there are 10 compounding periods when you invest semi-annually.

- Explain why there are 60 compounding periods when you invest monthly.

![]() Save your work to your course folder for reference in Share 2.
Save your work to your course folder for reference in Share 2.
Share 2
With a partner or group, discuss this question based on Try This 2.
- What do you notice about the effect of different compounding periods on interest earned?
Summarize your discussion by creating a statement that describes the effect of different compounding periods on the interest earned.
![]() Save this statement to your course folder.
Save this statement to your course folder.
1.19. Explore 4
Section 1: Simple and Compound Interest
Self-Check 2
- Based on what you have investigated in this lesson, determine which investment will earn the most interest.
- Do question 6 from “Build Your Skills” on page 273 of MathWorks 11. Answer
- Do question 7 from “Build Your Skills” on page 273 of MathWorks 11. Answer
It is now time to add new math terms to Mathematics 20-3: Glossary Terms.
In this lesson the new terms you will add are
- compound interest
- compound period
- annually
- semiannually
- quarterly
At this time, you may want to add the compound interest formula to your Formula Sheet.
1.20. Connect
Section 1: Simple and Compound Interest
Connect
Going Beyond
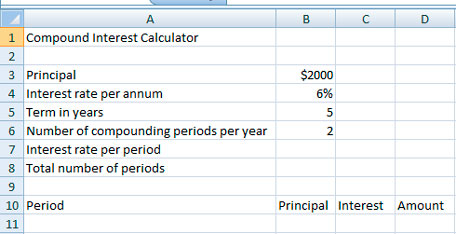
You can use the power of spreadsheets to calculate compound interest. Here is one way to set up such a spreadsheet.
Step 1: Copy the information from the image below onto your spreadsheet. This information shows an investment of $2000 invested for five years at 6% compounded semi-annually. You will be able to change the data easily to fit most situations.
© Microsoft Corporation. All Rights Reserved. Used with permission from Microsoft Corporation.
Step 2: Enter formulas for the interest rate per period and the total number of periods. Also, number the periods in Column A.
- In Cell B7, enter =$B$4/$B$. Format this cell for %.
- In B8, enter =$B$5*$B$6.
- In A11, enter 1.
- In A12, enter =A11+1.
- Highlight cells A12 to A20 and select Fill Down.
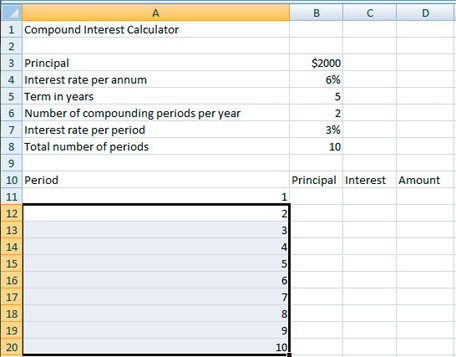
© Microsoft Corporation. All Rights Reserved. Used with permission from Microsoft Corporation.
Step 3: Enter the values and calculations for the first two interest periods into the noted cells.
- In B11, enter =$B$3.
- In C11, enter =B11*$B$7.
- In D11, enter =B11+C11.
- In B12, enter = D11.
- In C12, enter =B12*$B$7.
- In D12, enter =B12+C12.
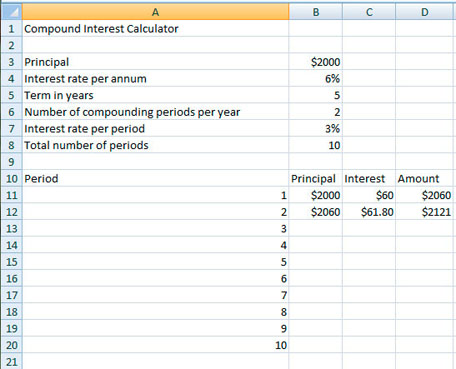
© Microsoft Corporation. All Rights Reserved. Used with permission from Microsoft Corporation.
Step 4: Complete the table. Highlight cells B12 to D20. Then, from the Calculate menu, select Fill Down.
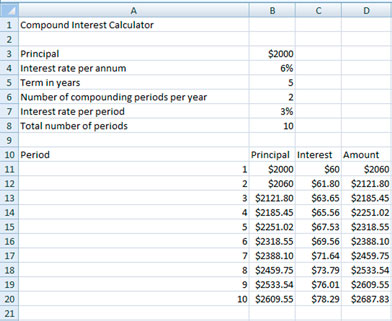
© Microsoft Corporation. All Rights Reserved. Used with permission from Microsoft Corporation.
Now, you can use your spreadsheet to solve most compound interest problems simply by entering the new data in cells B3 to B6. Everything else will update automatically. You will have to fill down the appropriate number of periods.
Use your spreadsheet to find the amount of an investment of $10 000 invested at 6% and compounded quarterly for two years.
Project Connection
You are now prepared to begin working on Step 3, the compound interest portion of the Section 1 Project: Capturing Your Interest!
![]() Make sure to save all your project work in your course folder to submit at the end of Section 1.
Make sure to save all your project work in your course folder to submit at the end of Section 1.
Lesson 2 Assignment
Your lesson assignment contains some problems for you to solve using knowledge gained during the lesson. Now you will have the chance to apply the concepts and strategies learned to a new situation. Show work to support your answers.
Open the Lesson 2 Assignment that you saved to your course folder and complete the questions.
1.21. Lesson 2 Summary
Section 1: Simple and Compound Interest
Lesson 2 Summary

iStockphoto/Thinkstock
In this lesson you examined compound interest on investments. To solve compound interest problems, you discovered that you had to know the annual interest rate, the number of compounding periods per year, the principal, and the investment term in years.
Compound interest is a much more powerful tool in making your money grow than simple interest because of the multiple compounding periods and reinvestment of the interest earned. Will you harness the power of compound interest?
1.22. Lesson 3
Section 1: Simple and Compound Interest
Lesson 3: The Rule of 72
 Focus
Focus
Albert Einstein is among the world’s greatest physicists and mathematicians. He’s the father of relativity and is popularly associated with the formula E = mc2. His formula links mass and energy and the harnessing of nuclear power.
In a related matter, Einstein claimed, “The most powerful force in the universe is compound interest.” In this lesson you will investigate the power of compound interest and discover and use a rule for estimating the length of time needed to double an investment.
Lesson Question
In this lesson you will investigate the following question:
- How can the Rule of 72 be used to solve compound interest problems?
Assessment
Your assessment for this lesson may include a combination of the following:
- course folder submissions from the Try This and Share sections of the lesson
- your contribution to the Mathematics 20-3 Glossary Terms and the Formula Sheet
- Lesson 3 Assignment (Save a copy of your lesson assignment to your course folder now.)
- the Project Connection
Materials and Equipment
- calculator
1.23. Launch
Section 1: Simple and Compound Interest
Launch
This section checks to see if you have the necessary background knowledge and skills required to successfully complete Lesson 3.
Complete the Are You Ready? questions. If you have difficulty or any questions, visit Refresher for a review or contact your teacher.
1.24. Are You Ready?
Section 1: Simple and Compound Interest
Are You Ready?
In this lesson you will apply your mental arithmetic skills. One skill in particular is identifying factors of composite numbers such as 72.
- What is meant by the term factor? Answer
- List all the factors of 72. Answer
- What is a composite number? Answer
If you answered the Are You Ready? questions without problems, move on to Discover.
If you found the Are You Ready? questions difficult, complete Refresher to review these topics.
1.26. Discover
Section 1: Simple and Compound Interest
Discover

Courtesy of First Nations University–Regina
In this section you will discover how to quickly estimate the time required to double an investment at a given rate of compound interest.
When Oscar entered Grade 1, his grandmother invested $2000 towards his education. The money was invested at 8% compounded annually over 12 years. This year, Oscar will use this money when he attends the First Nations University of Canada at Regina.
The following spreadsheet tracks the growth of this investment over 12 years.
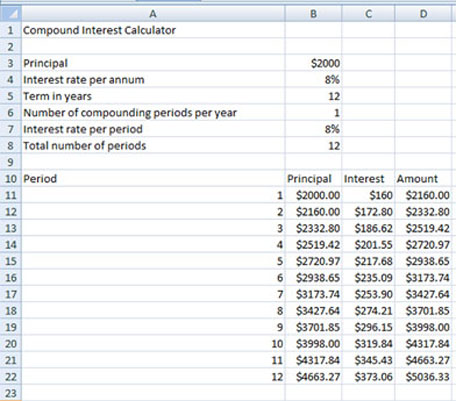
© Microsoft Corporation. All Rights Reserved. Used with permission from Microsoft Corporation.
Try This 1
- At the end of which investment year does the original $2000 double in value?
- Divide the number 72 by your answer to question 1. How does this answer compare to the interest rate of this investment?
- The answer to question 2 illustrates the Rule of 72. Can you suggest what is meant by the Rule of 72?
- About how many years would it take an investment to double in value at 6% compounded annually? Why?
![]() Save your answers to your course folder.
Save your answers to your course folder.
Share 1
Share your responses to the questions in Try This 1 with a classmate or group.
- How did your interpretation of the Rule of 72 compare with the opinions of other students?
- Why might there have been similarities and differences between the interpretations?
![]() If required, save a copy of your discussion in your course folder.
If required, save a copy of your discussion in your course folder.
1.27. Explore
Section 1: Simple and Compound Interest
Explore
In Discover you investigated the Rule of 72. You discovered that by using the Rule of 72, and given an annual interest rate that is compounded annually, you can estimate the time required for a given investment to double in value.
approximate number of years for the investment to double = ![]()
Example

iStockphoto/Thinkstock
During the ski season, Rose works as a ski instructor at Mont Tremblant in Québec. She has just invested $2000 of her savings at 4% compounded annually. Use the Rule of 72 to estimate the number of years it will take for Rose’s investment to double.
Solution
The annual interest rate = 4%
Use the Rule of 72:
Divide 72 by 4.
![]()
Rose’s investment will double in about 18 years.
You have seen the rule of 72 explained using the following formula:
approximate number of years for the investment to double = ![]()
But in Try This 1 you divided 72 by 9, which is the number of years it took the investment to double—not the interest rate! This is because the formula can be rearranged to estimate the annual interest rate if you know the doubling time for an investment.
interest rate as a percent = ![]()
In the next example you will explore how the Rule of 72 can be used to estimate the annual interest rate from the doubling time for an investment.
Example

Steve Mason/Photodisc/Thinkstock
Ron, who is 15 years old, loves snowmobiling. He has his eye on a model that costs $6000, and Ron would like to own the snowmobile by the time he turns 25. If he has $3000 in savings today, at what rate of interest should Ron invest the $3000 so that he will have $6000 in ten years?
Solution:
doubling time = 10 years
Use the Rule of 72:
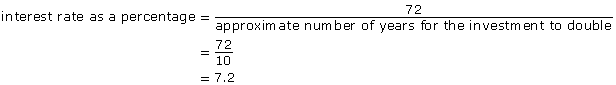
Ron should look for an investment that earns at least 7.2%.
1.28. Explore 2
Section 1: Simple and Compound Interest
Try This 2
- Search the Internet for a “Rule of 72 Calculator.” Find a calculator you like and use it to investigate the question in the next bullet.
- You have seen that the interest rate affects the doubling time of the investment, but does the amount of money you invest have any effect on the investment’s doubling time?
![]() Save your responses to your course folder.
Save your responses to your course folder.
Share 2
Share your Rule of 72 Calculator link, found in Try This 2, with a partner or group. Discuss the following question:
- What effect does the amount of money you invest have on the doubling time of the investment?
![]() If required, save a copy of the discussion to your course folder.
If required, save a copy of the discussion to your course folder.
Caution: Remember that the Rule of 72 uses percentages instead of the decimal equivalent. If you are given a rate of 0.06, you will first rewrite the rate as 6%.
1.29. Explore 3
Section 1: Simple and Compound Interest
Self-Check 1
- Complete the following table for compound interest investments using the Rule of 72. The first example, 4%, is completely done for your reference.
Interest Rate Doubling Time Your Calculation 4% 18 years 72 ÷ 4 = 18 24 years 12% 0.09 0.02 8 years 72 ÷ 6 = 12
Answer
- Karl has invested $1000 in a compound-interest bond earning interest at the rate of 0.024 per annum. Karl applied the Rule of 72 as follows.
72 ÷ 0.024 = 3000
At that rate, Karl says it will take 3000 years to double his investment. Is Karl correct? Why or why not? Answer
It is now time to add new math terms to Mathematics 20-3: Glossary Terms.
In this lesson the new term you will add is
- Rule of 72
At this time, you may want to add the Rule of 72 formula to your Formula Sheet.
1.30. Connect
Section 1: Simple and Compound Interest

Jupiterimages/Comstock/Thinkstock
Connect
Going Beyond
So you want to become a millionaire!
Suppose you had $7812.50 to invest, and you could earn 8% compounded annually. Estimate the number of years required for the $7812.50 to grow to $1 million.
Project Connection
You are now prepared to start Step 4 of the Section 1 Project: Capturing Your Interest! Make sure to save all your project work in your course folder to submit at the end of Section 1.
Lesson 3 Assignment
Your lesson assignment contains some problems for you to solve using knowledge gained during the lesson. Now you will have the chance to apply the concepts and strategies learned to a new situation. Show work to support your answers.
Open the Lesson 3 Assignment that you saved to your course folder and complete the questions.
1.31. Lesson 3 Summary
Section 1: Simple and Compound Interest
Lesson 3 Summary

In Focus you read that Einstein claimed that compound interest was the greatest power in the universe. Perhaps Einstein’s famous formula E = mc2 was really E = mc72!
In this lesson you explored the Rule of 72. You now have a tool for relating compound interest rates and the corresponding times required to double investments. Use this information to help you make wise investment decisions.
1.32. Lesson 4
Section 1: Simple and Compound Interest
Lesson 4: Comparing Simple and Compound Interest and Their Graphs
Focus

Adam Gault/Digital Vision/Thinkstock
Have you leafed through the financial pages of a newspaper or checked out an online financial newspaper or site? There you will see a variety of graphs indicating trends in markets, interest rates, the dollar, inflation, and the performance of individual stocks.
You have likely heard the saying, “A picture is worth a thousand words!” Nowhere is this comment more accurate than when investors want to see, at a glance, how their money is doing. Are the graphs rising or falling, and how steeply?
In this lesson you will compare simple and compound interest and graphically track the performance of these types of investments.
Lesson Questions
In this lesson, you will investigate the following questions:
- What is the difference in interest earned by simple versus compound interest?
- How do the graphs of simple and compound interest compare?
Assessment
Your assessment for this lesson may include a combination of the following:
- course folder submissions from the Try This and Share sections of the lesson
- your contribution to the Mathematics 20-3 Glossary Terms and the Formula Sheet
- Lesson 4 Assignment (Save a copy of your lesson assignment to your course folder now.)
- the Project Connection
Materials and Equipment
- calculator
- quarter-inch graph paper
- straight edge
1.33. Launch
Section 1: Simple and Compound Interest
Launch
This section checks to see if you have the necessary background knowledge and skills required to successfully complete Lesson 4.
Complete the Are You Ready? questions. If you have difficulty or any questions, visit Refresher for a review or contact your teacher.
1.34. Are You Ready?
Section 1: Simple and Compound Interest
Are You Ready?

Hemera Technologies/ PhotoObjects.net/Thinkstock
In this lesson you will apply your knowledge of simple interest and compound interest.
- Annie Lutaaq has just sold one of her carvings. With part of this money, Annie has bought a $100 bond that pays her simple interest at 5% per annum.
If you answered the Are You Ready? questions without problems, move on to Discover.
If you found the Are You Ready? questions difficult, complete Refresher to review these topics.
1.35. Refresher
Section 1: Simple and Compound Interest
Refresher
If you do not know the answers to the Are You Ready? questions or require more information, click on the play button to review comparing simple and compound interest. Choose the item called Simple and Compound Interest from the list.
Go back to Are You Ready? and try the questions again. Contact your teacher if you continue to have difficulty.
1.36. Discover
Section 1: Simple and Compound Interest
Discover
As you have already seen in Are You Ready?, compound interest can earn more interest than simple interest. In the following activity you will investigate the difference in interest earnings between simple and compound interest. You will visually represent this difference with a graph.
Try This 1
Compare what happens to $1000 over ten years if this money is placed in a simple interest investment, and what occurs if the cash is placed in a compound interest investment. You will use an interest rate of 20% for both investments—this rate is impossible to achieve but helps to emphasize the difference between compound and simple interest.
Fill in the remainder of this table by calculating the interest made and the total amount of money the investment is worth after each year. Remember that the interest will be added into the principal for compound interest but not for simple interest.
Year |
Simple Interest Investment | Compound Interest Investment | ||||
| Beginning Amount ($) | Interest Earned | Total (Accumulated) Amount | Beginning Amount ($) | Interest Earned | Total (Accumulated) Amount |
|
| 1 | $1000 | $200 | $1200 | $1000 | $200 | $1200 |
| 2 | $1200 | $200 | $1400 | $1200 | $240 | $1440 |
| 3 | $1400 | $200 | $1600 | $1440 | $288 | $1728 |
| 4 | $1600 | $200 | $1800 | $1728 | $345.60 | $2073.60 |
| 5 | $1800 | $200 | $2000 | $2073.60 | $414.72 | $2488.32 |
| 6 | $2000 | $200 | $2200 | $2488.32 | $497.66 | $2985.98 |
| 7 | $2200 | $2985.98 | ||||
| 8 | ||||||
| 9 | ||||||
| 10 | ||||||
- Based on the table, in the first year how much did each of the investments earn? Which one earned more?

- By the end of ten years, did the simple interest investment or the compound interest investment earn more interest?
- Using graph paper or a computer program, create a double-bar graph of the total amounts for the simple interest GIC and the compound interest GIC.


- If you connected the tops of the bars for the simple interest investment, would a straight line or a curved line be best?
- If you connected the tops of the bars for the compound interest investment, would a straight line or a curved line be best?
- Use your graph to predict the accumulated total for the simple and compound interest in the eleventh year.
![]() Save a copy of your responses to your course folder.
Save a copy of your responses to your course folder.
Share 1
Share your answers to Try This 1 with a partner or group. After you have shared your answers, discuss the following:
- How does the shape of the bar tops in a simple interest graph differ from a compound interest graph?
- Suggest reasons that could explain this difference in shape.
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
1.37. Explore
Section 1: Simple and Compound Interest
Explore
You will now look closer at the reasons for the shape of the graphs of simple and compound interest investments.
Try This 2
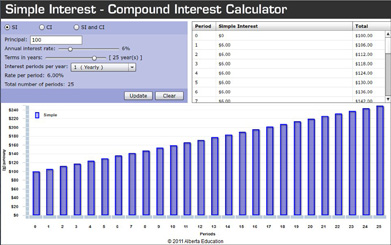
A spreadsheet is a useful tool for comparing the accumulated totals for simple interest and compound interest investments.
- Using the Simple Interest-Compound Interest Calculator, experiment with different interest rates, interest periods, and terms for investments of your choice. Pay careful attention to how the graphs change each time you change the data.
- Complete this Compound and Simple Interest Drag and Drop based on your observations from using the previous spreadsheet.

- Why do the bar heights of compound interest graphs each form a curved increasing line while the bars of simple interest graphs form a straight line?

Simple Interest Bars: The bars forming the graph for simple interest line up in a straight line because the interest added to each column is always based on the original investment. The interest added is constant, so the slope of the line the bars form is also constant.
Compound Interest Bars: The heights of bars forming the graph for compound interest grow at ever-increasing rates because interest is calculated on interest that has been added each year. The interest added is increasing so the slope of the line created by the bars is constantly increasing and creating a curved line.
1.38. Explore 2
Section 1: Simple and Compound Interest
The graph of a compound interest investment shows growth described by a curved increasing line—this type of growth is called exponential growth. The graph of a simple interest investment shows growth described by a straight line: this type of growth is called linear growth.
In Try This 2 you investigated the spreadsheet graphs for investments earning simple and compound interest over short periods of time. Here is another example of graphs showing the power of compound interest over a much longer period of time.
Notice again that the simple interest graph forms a straight line, while the compound interest graph sweeps upward to the right.
In this example, $1000 is invested at 6% for 50 years. What is the difference in the final amounts?
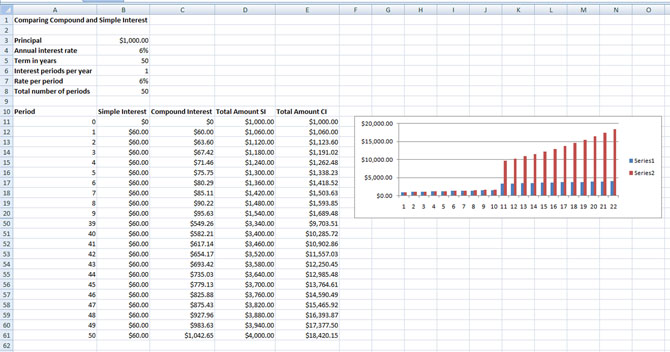
© Microsoft Corporation. All Rights Reserved. Used with permission from Microsoft Corporation.
The difference in earnings between simple interest and compound interest is $14 420.15, which is a huge difference over 50 years. This example really shows the power of compound interest.
1.39. Explore 3
Section 1: Simple and Compound Interest
Self-Check 1
Use the Simple Interest - Compound Interest Calculator to answer the following questions.
- Suppose you had $4000 to invest. Compare the difference in earnings between a simple and a compound investment after 20 years for an annual interest rate of 4%. Assume the interest period is annual. Answer
- Repeat question 1, but assume interest is calculated semi-annually. Explain why the results are the same for simple interest but different for compound interest. Answer
- Explain why you would be able to connect the midpoint of each bar of the simple interest graph without lifting, moving, or rotating your ruler or some other similar tool. Answer
- Explain why you would not be able to connect the midpoint of each bar of the compound interest graph without lifting, moving, or rotating your ruler or some other similar tool. Answer
- Explain why you would be able to connect the midpoint of each bar of the simple interest graph without lifting, moving, or rotating your ruler or some other similar tool. Answer
It is now time to add new math terms to Mathematics 20-3: Glossary Terms.
In this lesson the new terms you will add are
- exponential growth
- linear growth
1.40. Connect
Section 1: Simple and Compound Interest
Connect
Going Beyond
So, do you still want to become a millionaire?
Suppose you had saved $2000 from your part-time job and invested this sum at 3% compounded annually for 50 years. At the end of 50 years, without investing a cent more, you would have $8767.81. But suppose you saved $100 a month and added $1200 to your investment at the end of each year.
Use the Simple Interest - Compound Interest Calculator to answer the following questions.
- Change the yearly investment to $1200 to see how much money you would have.
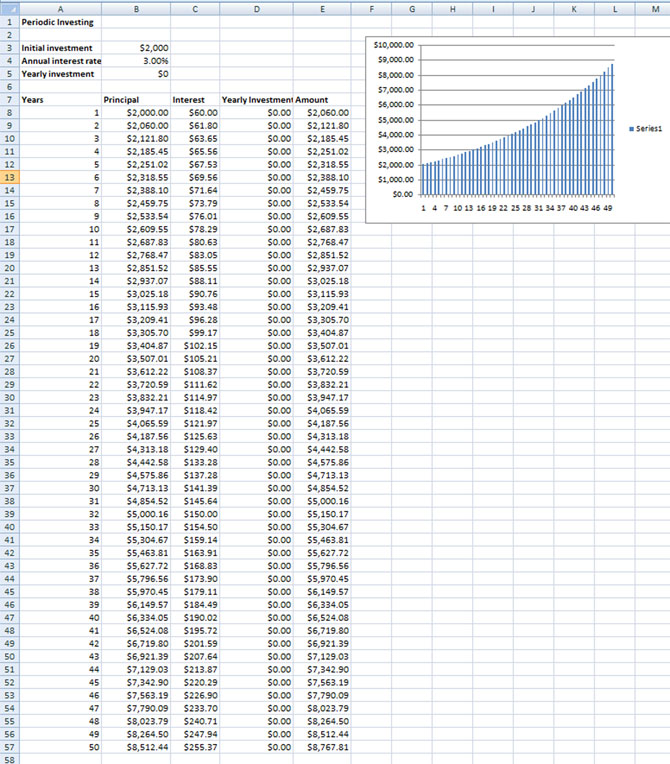
© Microsoft Corporation. All Rights Reserved. Used with permission from Microsoft Corporation.
The result may have surprised you. Now try changing the initial investment, interest rates, or annual investment amounts to see how you can become a millionaire.
Project Connection
You are now prepared to finish the Section 1 Project: Capturing Your Interest! Begin Steps 5 and 6, and then submit the entire completed project to your teacher.
Lesson 4 Assignment
Your lesson assignment contains some problems for you to solve using knowledge gained during the lesson. Now you will have the chance to apply the concepts and strategies learned to a new situation. Show work to support your answers.
Open the Lesson 4 Assignment that you saved to your course folder and complete the questions.
1.41. Lesson 4 Summary
Section 1: Simple and Compound Interest

Chris Stein/Lifesize/Thinkstock
Lesson 4 Summary
Successful investing means being able to see the big picture. In this lesson the big picture was graphically comparing financial growth through simple and compound interest. You discovered that the bars in a simple interest graph lined up in a straight line, while those for compound interest swept upward to the right in a curve that grew steeper and steeper. This characteristic of compound interest is due to exponential growth.
1.42. Section 1 Project
Section 1: Simple and Compound Interest
Section 1 Project: Capturing Your Interest!

iStockphoto/Thinkstock. Currency used with the permission of the Bank of Canada
You have probably read that Canadians don’t save enough money for retirement. But saving for retirement isn’t the only reason to set some money aside. You may wish to buy a car or house in the future. Also, having a nest egg protects you in emergencies. Savings give you the freedom to make choices such as training for a new job, moving to a different city, travelling, or helping your family.
But saving is only one part of the equation. Once you have saved some money, how will you invest these funds? Banks and credit unions offer a variety of investment choices. In this project you will explore two of those choices—simple interest and compound interest.
For this project you will assume you have $10 000 to invest. What will you do?
Goal
Your goal for this project is to explore simple and compound-interest options for a $10 000 investment.
Time
The aim is to complete this project in less than ![]() hours. Each lesson in the section will direct you to complete at least one of the steps.
hours. Each lesson in the section will direct you to complete at least one of the steps.
Steps
- Contact a local bank or credit union (in person, online, or use the guided search information in bank links from the Module 1: Section 2 Project: Banking 101).
- What is the best rate of interest you might receive on an investment of $10 000? These choices might include bonds, savings accounts, and Guaranteed Investment Certificates.
- Report your findings by filling out the following information.
Type of Investment:______________________
Best Interest Rate:___________________________
Interest Period: __________________________
Term of Investment: _________________________
- What is the best rate of interest you might receive on an investment of $10 000? These choices might include bonds, savings accounts, and Guaranteed Investment Certificates.
- Assume you are able to invest at the best rate of simple interest for five years. Use the simple interest formula, I = Prt, and A = P + I to determine the sum (interest and principal) you would have at the end of five years. Show all your steps.
- Assume you are able to invest at the best rate of compound interest for five years. Use the compound-interest formula,
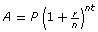 , to determine the sum (interest and principal) you would have at the end of five years. Show all your steps.
, to determine the sum (interest and principal) you would have at the end of five years. Show all your steps.
- Apply the Rule of 72 to estimate how long it will take to double your money.
- Based upon the rates you used, which investment option (simple or compound) is the better choice? Explain your answer.
- Use the Simple Interest - Compound Interest Calculator to create graphs showing the growth of each investment (simple and compound) over the five-year term. The interest rates are set at 5% per annum. Change these amounts to the rates you used in your calculations. Attach a copy of each graph, and include them in your project summary.
How You Will Be Evaluated
Your teacher will use this rubric to evaluate your report.
| FOLLOWING YOUR INTEREST RUBRIC | ||||
| Score | Required Concepts |
Connections | Mathematical Calculations | Communication for Final Presentation |
3 Exceeds Acceptable Standard |
All of the project requirements have been addressed. | Explanations show a detailed understanding of connections between the mathematics of simple and compound interest and their use in this project. |
All required mathematical representations are completed, correct, and support the explanations. | The work is presented in a neat, clear, and organized fashion that is easy to read and/or see. |
2 Meets Acceptable Standard |
Most of the project requirements have been addressed. | Explanations show an adequate understanding of connections between the mathematics of simple and compound interest and their use in this project. | There may be some minor math/calculation errors or flaws in reasoning. | The work is presented in an organized fashion but may be hard to read at times. |
1 Below the Acceptable Standard |
Few of the project requirements have been addressed. | The response shows only a little understanding of connections between the mathematics of simple and compound interest and their use in this project. | There are major math/calculation errors or serious flaws in reasoning. | The work appears sloppy and/or unorganized. It is hard to know what information goes together. |
0 Does Not Meet the Minimum Standard |
A minimal number of the project requirements have been addressed. | The response shows a lack of understanding of the connections between the mathematics of simple and compound interest and their use in this project. | There is no understandable attempt at using mathematical representations. | There is no understandable presentation of project work. |
Total Score /18 |
/3 | /3 × 2 = /6 | /3 × 2 = /6 | /3 |
1.43. Section 1 Summary
Section 1: Simple and Compound Interest
Section 1 Summary

iStockphoto/Thinkstock
“Oh, they don’t have to worry; they have pots of money!” Is this a familiar phrase? Have you considered that perhaps they have overflowing pots of money due to wise investments?
During the Section 1 Project: Capturing Your Interest!, you examined how simple and compound interest offered by banks can make your own money grow differently. After exploring investment growth, you are now in a position to make informed decisions about your own savings.
In Lessons 1 and 2 you explored the formulas for simple and compound interest. You applied the Rule of 72 in Lesson 3 to find how long it would take to double your money. And in Lesson 4 you examined the growth of investments over time by analyzing graphs. All the skills you acquired are fundamental to your financial growth. It’s now your turn to watch your money tree grow bigger and stronger.