Section 1
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-3 SS |
| Book: | Section 1 |
| Printed by: | Guest user |
| Date: | Tuesday, 2 December 2025, 7:01 AM |
Description
Created by IMSreader
Table of contents
- 1. Section 1
- 1.1. Lesson 1
- 1.2. Launch
- 1.3. Are You Ready?
- 1.4. Refresher
- 1.5. Discover
- 1.6. Explore
- 1.7. Explore 2
- 1.8. Explore 3
- 1.9. Connect
- 1.10. Lesson 1 Summary
- 1.11. Lesson 2
- 1.12. Launch
- 1.13. Are You Ready?
- 1.14. Refresher
- 1.15. Discover
- 1.16. Explore
- 1.17. Explore 2
- 1.18. Explore 3
- 1.19. Explore 4
- 1.20. Connect
- 1.21. Lesson 2 Summary
- 1.22. Lesson 3
- 1.23. Launch
- 1.24. Are You Ready?
- 1.25. Refresher
- 1.26. Discover
- 1.27. Explore
- 1.28. Explore 2
- 1.29. Explore 3
- 1.30. Explore 4
- 1.31. Explore 5
- 1.32. Connect
- 1.33. Lesson 3 Summary
- 1.34. Section 1 Summary
1. Section 1
Section 1: Slope—Physical Objects
Section 1 Introduction

© Paula Becattini/20902898/Fotolia
Castles were built as places of safety for their owners. In the photo above you can see vertical walls and the land rising steeply to the castle. These features helped to make attacks on the castle difficult.
In this section you will look at angled surfaces and ways to describe them. As you consider slopes, you will also consider safety. For example, how does the slope of a roof relate to the safety of people building the roof, or how does a road grade relate to the safety of trucks going down the road?
In the Module 3 Project: Luge Track Comparison, you will compare the slopes of two Olympic sliding tracks. You will consider how the slopes relate to the safety of the athletes who use the track.
1.1. Lesson 1
Section 1: Slope—Physical Objects
Lesson 1: Slope in the Real World
Focus

Comstock/Thinkstock
Have you heard of “Roof Over Your Head Day?” This day occurs every December 3 and was organized to let everyone appreciate how fortunate people are who have a home.
Most roofs in Canada are not flat. How would you describe the shape of most roofs in Canada? Some words you might use are angled, steep, or sloped. The most common reason for roofs not being flat is to help snow slide off. This helps keep roofs from collapsing under the snow’s weight. In many parts of Canada, where snowfalls of two or three feet are common, this is an important safety issue.
If you build a roof, some questions you have to consider are these:
- What are the building code requirements?
- Are there any height restrictions set by the community?
- Which type of roof requires less building materials?
In this lesson you will explore ways to describe slopes, identify slopes, and think about the safety issues that surround slopes.
Lesson Questions
In this lesson you will investigate the following questions:
- How can slopes be identified and described?
- When dealing with slopes, what safety features are necessary?
Assessment
Your assessment for this lesson may include a combination of the following:
- course folder submissions from the Try This and Share sections of the lesson
- your contribution to Mathematics 20-3: Glossary Terms
- Lesson 1 Assignment (Save a copy of your lesson assignment document to your course folder now.)
- the Project Connection
In this course you may come across Self-Check questions, Try This questions, and other activities that may or may not be assessed.
Remember that these questions and activities provide you with the practice and feedback that you need to successfully complete this course. You should respond to all the questions and place those answers in your course folder. Your teacher may wish to view the work that you have stored in your course folder to check on your progress and to see if you require assistance.
Materials and Equipment
- ruler(s)
- pencil
- measuring tape
- stairs
Time
This lesson has been designed to take 150 minutes; however, it may take more or less time depending on how well you are able to understand the lesson concepts. It is important that you progress at your own pace based on your own learning needs.
1.2. Launch
Section 1: Slope—Physical Objects
Launch
This section checks to see if you have the necessary background knowledge and skills required to successfully complete Lesson 1.
Complete the following Are You Ready? questions. If you have difficulty or any questions, visit Refresher for a review or contact your teacher.
1.3. Are You Ready?
Section 1: Slope—Physical Objects
Are You Ready?
- Where does a vertical line point? Answer
- Where does a horizontal line point? Answer
- What angle is formed when a vertical line meets a horizontal line? Answer
- What is the longest side of a right triangle called? Answer
If you answered the Are You Ready? questions without problems, move on to Discover.
If you found the Are You Ready? questions difficult, complete Refresher to review these topics.
1.5. Discover
Section 1: Slope—Physical Objects
Discover
Try This 1
Look at these three photos and consider the questions that follow.

wheelchair ramp: Hemera/Thinkstock; bike rider: Hemera/Thinkstock; stairs: iStockphoto/Thinkstock
- Could you easily go up and down in each case?
- Which photo seems to show the steepest slope?
- What activity would be the most dangerous?
- Fill in the following chart. It will help you describe similarities and differences in the photos.
Similarities Differences
- Think about and record some safety issues related to the activities. Use the following chart to record your ideas.
Safety Issues
![]() Save both charts in your course folder to use in the following Share 1 activity.
Save both charts in your course folder to use in the following Share 1 activity.
Share 1
Share your charts from Try This 1 with a partner or with a group of people.
- Compare your charts with the other charts.
- Explain reasons for any similarities and differences between the charts.
As you work on this Share section, refer to the Share Rubric. The rubric will help you understand what your teacher expects of you.
1.6. Explore
Section 1: Slope—Physical Objects
Explore
In Discover, you saw a variety of photos with one thing in common: slope. The images show a wheelchair ramp, a bike jump, and stairs up the outside of a temple. What problems could result if the slope of the wheelchair ramp were three times steeper than what is shown in the photo? At what point does a slope become too steep?
Try this experiment. Place a pencil about 1 in from the end of a 12-in ruler, as shown in the photo below. How high can you lift that end of the ruler before the pencil slides or rolls down?

How can you describe the steepness right before the pencil begins to move?
1.7. Explore 2
Section 1: Slope—Physical Objects
Try This 2
Architects and carpenters must pay attention to specified building and safety codes when designing and building steps and staircases. In this activity you will investigate whether the steps or stairs you use daily meet Alberta’s building codes.
Find some steps or stairs that are uniform (the same size) and that do not have a nosing (an overhang). Make sure that the steps are the same size.

iStockphoto/Thinkstock
The stairs should look like this.

Polka Dot/Thinkstock
- Use a measuring tape or ruler to measure two or three of the steps. Record your answers in the following chart.
Step Vertical Distance Horizontal Distance 1
2
3
Total
- Do you notice a pattern between each step’s vertical and horizontal distance?
- What do you expect the vertical and horizontal measurements to be for each of the remaining steps?
- What is the total vertical height of the steps you measured?
- What is the total horizontal length of the steps you measured?
- What calculation could you make to find the total vertical distance of the staircase (all of the steps) without measuring the rest of the steps?
- What calculation could you make to find the total horizontal distance of the staircase (all of the steps) without measuring the rest of the steps?
- Sketch your staircase. Label the vertical and horizontal distance of one step and the total vertical and total horizontal distance of the entire staircase.
Look at the following diagram and note the words used to describe individual steps and the entire staircase. This is the terminology that architects and carpenters use when building steps and staircases.
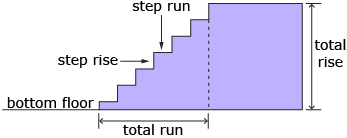
- Label your sketch using the same words as those in the diagram.
- Alberta’s building codes state that the minimum rise for a step is 125 mm, and the maximum rise is 200 mm. The minimum run is 210 mm, and the maximum run is 355 mm. Do your steps meet the building codes?
- How can you show the total distance travelled up a staircase using one line? Draw this line on your sketch. Does your line look like the slope line in the following diagram?
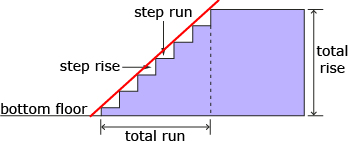
![]() Save your work in your course folder for future reference.
Save your work in your course folder for future reference.
1.8. Explore 3
Section 1: Slope—Physical Objects
In Try This 2 you drew a line on the staircase sketch to clearly see the total distance travelled. The line was angled because it had to show the total horizontal and vertical distance travelled. The following image describes this angled line as the slope of the staircase.
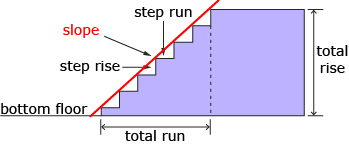
Did You Know?
In the image, the red line representing slope is made up of the horizontal distance (the run) and the total vertical distance (the rise) the line travels. This is the definition of slope.
Read page 12 in MathWorks 11.
Did You Know?
As you read through “Explore the Math,” think about the following questions:
- What other words mean the same as slope?
- What is the slope formula?
- What letter is used to represent slope?
- What does the Greek symbol “Δ” mean?
An understanding of slope is very important for a contractor who builds and designs houses. As you read “Math on the Job” on page 12 of the textbook, think about the following questions:
- What do the 1 and the 4 represent in a slope of
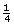 ?
?
- What are the consequences for Gilles and the homeowners if Gilles does not follow the building codes?
Self-Check 1
So far, you have learned what slope is, how slope is determined, and some safety concerns associated with slope. Test yourself with Slope Questions to see how much you remember.
It is time to add new math terms, definitions, and examples/notes to your Mathematics 20-3: Glossary Terms document. Complete the missing pieces of the document, and save it to your desktop. Note that some terms, definitions, and examples/notes have already been provided in the document.
In this lesson the new terms you will add are the following:
- rise
- run
- slope
1.9. Connect
Section 1: Slope—Physical Objects
Connect
Going Beyond
Use your favourite Internet search engine to extend your learning by researching the origins of the symbol m for slope. In your search, identify possible reasons for the choice of symbol.

Comstock/Thinkstock
Project Connection
Luge is a sport that depends completely on slopes. The slope of a luge track can vary between different corners and different tracks. In your Module 3 Project: Luge Track Comparison, you will be comparing the luge track at Whistler Sliding Centre with the track at Canada Olympic Park.
You are now prepared to read the project introduction and work on Step 1 of the Module 3 Project: Luge Track Comparison. Save all project work in your course folder to submit at the end of Section 2.
Lesson 1 Assignment
Your lesson assignment contains some problems for you to solve using the knowledge gained during the lesson. Now you will have the chance to apply the concepts and strategies learned to a new situation. Show work to support your answers.
Open the Lesson 1 Assignment that you saved to your course folder and complete the questions.
1.10. Lesson 1 Summary
Section 1: Slope—Physical Objects
Lesson 1 Summary

iStockphoto/Thinkstock
In this lesson you saw slope in roofs, stairs, ramps, pieces of equipment, and in nature. You shared and discussed ways of describing slope and the safety issues surrounding slopes. You also learned that the formula used to calculate slope is made up of vertical distance, called the rise, and horizontal distance, called the run.
In Lesson 2 you will use your knowledge of slope and safety to calculate slope to ensure safety standards are met.
1.11. Lesson 2
Section 1: Slope—Physical Objects
Lesson 2: Calculating and Understanding Slope
Focus

© NaDi/25133759/Fotolia

Comstock/Thinkstock
Trucks, especially those with big loads, have to slow down at some points along roads. This is especially true when the vehicles are being driven downhill. To help the truck drivers, there are signs telling them
- the road’s steepness
- the speed they should be driving
- how long the stretch of road is that they need to slow down for
In Lesson 1 you learned that slopes can be found all around. You also learned that slope is defined as ![]() In this lesson you will make calculations to find slope. You will also decide what slope values tell you about the steepness of a slanted object.
In this lesson you will make calculations to find slope. You will also decide what slope values tell you about the steepness of a slanted object.
Lesson Questions
In this lesson you will investigate the following questions:
- How is slope calculated?
- Under what conditions will a slope be constant, zero, or undefined?
Assessment
Your assessment for this lesson may include a combination of the following:
- course folder submissions from the Try This and Share sections of the lesson
- your additions to the Math 20-3: Glossary Terms and the Formula Sheet
- Lesson 2 Assignment (Save a copy of your lesson assignment document to your course folder now.)
- the Project Connection
Materials and Equipment
- calculator
- graph paper (1 cm × 1 cm)
1.12. Launch
Section 1: Slope—Physical Objects
Launch
This section checks to see if you have the necessary background knowledge and skills required to successfully complete Lesson 2.
Complete the following Are You Ready? questions. If you have difficulty or any questions, visit Refresher for a review or contact your teacher.
1.13. Are You Ready?
Section 1: Slope—Physical Objects
Are You Ready?
- Reduce the following fractions to their simplest (lowest) forms. Also give them as a decimal to two places.
If you answered the Are You Ready? questions without problems, move on to Discover.
If you found the Are You Ready? questions difficult, complete Refresher to review these topics.
1.15. Discover
Section 1: Slope—Physical Objects
Discover
In the following Try This activity you will explore slope at various points along different graphs of lines and curves.
Try This 1
Complete the table for Slopes 1, 2, and 3 by finding the slope for multiple points on each graph.
| Slopes of Lines | ||||||||
| Slope 1 | Slope 2 | Slope 3 | ||||||
| Point 1 | Point 2 | Slope | Point 1 | Point 2 | Slope | Point 1 | Point 2 | Slope |
| (−6, −8) | (2, 8) | 2 | ||||||
- What did you notice about the slopes of lines 1, 2, and 3? Did you observe any patterns?
Share 1
Discuss your observations and answer to Try This 1 with a partner or with a group of people.
- What similar patterns were observed?
- Did anyone identify a pattern different from yours? Explain.
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
In Explore you will calculate slopes in different contexts.
1.16. Explore
Section 1: Slope—Physical Objects
Explore
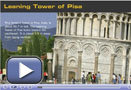
In Discover you found the slope for various points on a graph. Did you notice how the slopes were calculated? Click on the Leaning Tower of Pisa example to see how a slope is calculated.
Try This 2
In the following applet you will work through steps to see how a ramp’s slope is calculated. As you work through the applet, pay attention to the rise and run and how these measurements are identified for an incline. Are they found in the same way as they were in the Leaning Tower of Pisa example?
Open Rise, Run, and Slope, and then select Slope as Rise Over Run. Follow the instructions to complete pages 1 to 5 of the activity. (Don't close this activity when you finish page 5—you will work on page 6 later in the lesson.)
As you may have noticed in Try This 2, slope can be calculated even when numbers are not given. This calculation can be done by placing graph paper or a grid on a diagram and counting the squares.
You can also use your ruler to measure the rise and run.
1.17. Explore 2
Section 1: Slope—Physical Objects
Self-Check 1
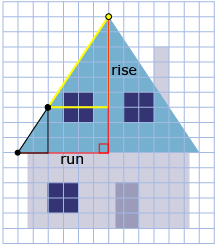
- Calculate the slope between two different places on the diagram above.
- How do the two slopes on the same line compare? Answer
Refer back to Discover. What patterns did you discover for the slope of lines? You may have noticed that the slope of a curved line changed. The slope on the curved line depended on where you measured the rise and run on the curve. This slope was very different than the slope of a straight line. The slope of a straight line is the same no matter where you measure the rise and run. This slope is called a constant slope.
A straight line has a constant slope. A curved line does not.
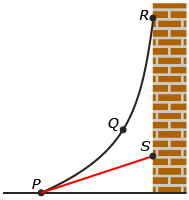
Self-Check 2
Answer true or false to questions 1 and 2.
- Line segment PS would have a constant slope. Answer
- Line segments PQ, QR, and PR would have different slopes. Answer
- Calculate the slope of PS. How did you calculate the slope? Answer
1.18. Explore 3
Section 1: Slope—Physical Objects
Share 2
Ninety-five percent of avalanches occur on mountains with slopes between ![]() and
and ![]() .
.
With a partner or with a group of people, discuss the following questions:
- Is an avalanche likely to occur in the right graphic? Explain.
- Is an avalanche likely to occur in the left graphic? Explain.
![]() Save a summary of your conclusions to your course folder.
Save a summary of your conclusions to your course folder.
The sides of the Egyptian pyramids had to be built at a specific, constant slope or these structures would collapse on themselves.

Photodisc/Thinkstock
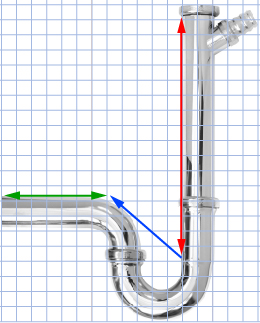
iStockphoto/Thinkstock
Look at the partial diagram of pipes to the right. The water could flow
- vertically (red arrow)
- in a loop where it would flow horizontally and vertically (blue arrow)
- horizontally (green arrow)
Calculate the slope of the blue, red, and green lines. Are any of the lines more challenging to calculate than others?
You may have found it challenging to calculate the slope of the green horizontal line since there was no rise to measure. The run may have been hard to measure for the red line.
Try This 3
Explore the Roller Coaster activity, which describes the slope of a car on a roller coaster. Pay attention to where the slope is equal to zero or undefined.
1.19. Explore 4
Section 1: Slope—Physical Objects
Self-Check 3
Complete each sentence by filling in the blanks.
- When calculating the horizontal slope, the value of the _________ is always zero and, therefore, the slope is always _____________. Answer
- When calculating the vertical slope, the value of the _________ is always zero and, therefore, the slope is always _____________. Answer
It is now time to add new math terms to your Mathematics 20-3: Glossary Terms document.
In this lesson the new terms you will add are
- undefined slope
- zero slope
- grid
- constant slope
At this time, you may want to add the slope formula to your Formula Sheet.
1.20. Connect
Section 1: Slope—Physical Objects
Connect
Going Beyond
In some cases, the rise or the run needs to be found before the slope can be calculated. Click on the play button to the left to take you to Rise, Run, and Slope. Then, select Slope as Rise Over Run, the activity you began in Explore. Do page 6. You will need to use the Pythagorean theorem to help you find the rise.
Refer to the Pythagorean Theorem definition from the Mathematics Glossary if you need some help remembering the theorem.
Project Connection
You are now prepared to begin working on Step 2 of the Module 3 Project: Luge Track Comparison. Make sure to save all your project work in your course folder to submit at the end of Section 2.
Lesson 2 Assignment
Your lesson assignment contains some problems for you to solve using the knowledge gained during the lesson. Now you will have the chance to apply the concepts and strategies learned to a new situation. Show work to support your answers.
Open the Lesson 2 Assignment that you saved to your course folder and complete the questions.
1.21. Lesson 2 Summary
Section 1: Slope—Physical Objects
Lesson 2 Summary
In this lesson you discovered how to calculate slope. You also described situations where the slope is constant, equal to zero, or undefined. You viewed each of these situations in relation to a roller coaster.
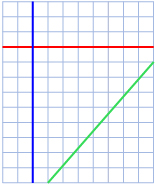
Horizontal lines, like the red line segment, have a slope of zero because there is no rise.
![]()
Vertical lines, like the blue line segment, have an undefined slope because there is no run.
Oblique lines, like the green line segment, have slope found by dividing rise by run.
You saw that a straight line has a constant slope. You also determined that curved lines have slopes that change depending on what points you use to calculate their slopes.
1.22. Lesson 3
Section 1: Slope—Physical Objects
Lesson 3: Implications of Slope—Safety and Use
Focus

iStockphoto/Thinkstock
Water parks are great fun for families and people of any age. How do slide designers make sure everyone has a fun time? Slides that are fun for a young child will be quite boring for most people aged 18. Meanwhile, slides intended for adults are very dangerous for some Grade 1 children. What factors influence slide design?
In this lesson you will explore some of these design factors as you compare slopes and use these comparisons to discuss safety and functionality.
Lesson Questions
In this lesson you will answer the following questions:
- How can the difference between two slopes be described?
- What safety and functionality issues are created by a slope?
Assessment
Your assessment for this lesson may include a combination of the following:
- course folder submissions from the Try This and Share sections of the lesson
- your contribution to the Math 20-3 Glossary Terms and the Formula Sheet
- Lesson 3 Assignment (Save a copy of your lesson assignment document to your course folder now.)
- the Project Connection
1.23. Launch
Section 1: Slope—Physical Objects
Launch
This section checks to see if you have the necessary background knowledge and skills required to successfully complete Lesson 3.
Complete the following Are You Ready? questions. If you have difficulty or any questions, visit Refresher for a review or contact your teacher.
1.24. Are You Ready?
Section 1: Slope—Physical Objects
Are You Ready?

red sign: AbleStock.com/Thinkstock; yellow sign: iStockphoto/Thinkstock
Look at the two photos of signs that indicate road grades. Note that the road’s slope is given as a percentage. Review your skills by rewriting the percentages in the following forms:
- fraction
- fraction in simplest form
- fraction as a ratio
- decimal to the nearest hundredth (two places)
| Grade (in percentage) | Fraction | Fraction in Simplest Form | Ratio Form | Decimal Form |
| 8% | ||||
| 7% |
If you answered the Are You Ready? questions without problems, move on to Discover.
If you found the Are You Ready? questions difficult, complete Refresher to reviewthese topics.
1.25. Refresher
Section 1: Slope—Physical Objects
Refresher
If you don’t know the answers in Are You Ready?, or require more information, then use the following information to review concepts.
To review percentages, go to Percent.
For help with decimals, go to Decimals.
In addition to being written in fraction or decimal form, slope can also be written as a ratio. Look at the following example of ratio notation to see a number of ways ratio can be expressed. (This material comes from an Individual Learning Module for carpentry. You can check out the whole document at Calculating Ratio and Proportion, Mechanical Advantage and Percentage if you are interested.)
Ratio Notation
Suppose you are comparing the ratio of hammers (2) to screwdrivers (6) in your toolbox.

The ratio can be stated in one of three common ways:
- 2 to 6,
- 2:6 and
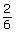
All of these ratios are read the same way: the ratio is 2 to 6.
Because a ratio can be expressed as a fraction, it can also be reduced to its simplest terms. Reducing the ratio of ![]() to its simplest terms gives you
to its simplest terms gives you ![]() . This means that there is 1 hammer for every 3 screwdrivers in your toolbox.
. This means that there is 1 hammer for every 3 screwdrivers in your toolbox.
| Note |
| The order in a ratio matters: a ratio of 1:3 is not the same as 3:1. |
Go back to Are You Ready? and try the questions again. Contact your teacher if you continue to have difficulty with the questions.
1.26. Discover
Section 1: Slope—Physical Objects
Discover

iStockphoto/Thinkstock

iStockphoto/Thinkstock
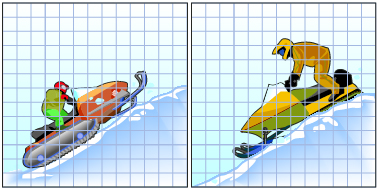
Water slides come in all heights and lengths. These measurements will determine how fast you can go and how long your ride will be. In Try This 1 you will investigate slopes of water slides.
Try This 1
- Calculate the slope of the green water slide in the first photo and the slope of the blue water slide in the other photo. Write your answer in fraction form
 .
.
- Describe the similarities and differences between the two slopes.
- Which slide do you think would be the fastest? What is the fastest slide's slope?
Share 1
Once you have completed the Try This 1 activities, discuss the following questions with a partner or with a group of people.
- What is the relationship between the value of the slope and the steepness of the slide?
- What do you notice about the steepness of the water slides when the rise and run of the slope are switched?
![]() Place a summary of your discussion and responses to the questions in your course folder.
Place a summary of your discussion and responses to the questions in your course folder.
1.27. Explore
Section 1: Slope—Physical Objects
Explore

Comstock/Thinkstock
In Focus you saw that water slides come in all shapes and sizes. You also thought about the factors that determine how steep the slides are. In Discover you began to calculate the slopes of two water slides, and you may have noticed a similarity between them. The rise of one slide was equal to the run of the other.
The steeper green slide has a slope of ![]() and the shallower blue slide has a slope of
and the shallower blue slide has a slope of ![]() . You may have noticed that the larger the slope value, the steeper the slope.
. You may have noticed that the larger the slope value, the steeper the slope.
A water slide is a slippery slope. You don’t want your roof to be a slippery slope.
Carpenters refer to a roof’s slope as the pitch. Many factors influence how steep a roof is built. The pitch of a roof is found by measuring the amount the roof rises for every 12 in, or 1 ft, of run.
Compare the two roof pitches in the following graphics. The runs are both 12 in, so the rise is what determines the slope’s steepness. The pitch (a 10-in rise for every 12-in run) is much steeper than the ![]() roof pitch. When the run length is kept standard (12 in), what determines the roof's steepness? It's the rise: the higher the rise, the steeper the slope.
roof pitch. When the run length is kept standard (12 in), what determines the roof's steepness? It's the rise: the higher the rise, the steeper the slope.
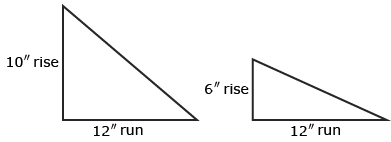
Example
In the activity Roof Pitch, the pitch is calculated using a grid.
1.28. Explore 2
Section 1: Slope—Physical Objects
Self-Check 1
Read question 2 on page 20 of Mathworks 11, and answer the following questions.
- What is the standard number of inches of run used to calculate the slope of a roof? Answer
- Express the slope of a 6:12 roof in fraction form as
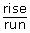 . Answer
. Answer
- Calculate the pitch of the three roofs from question 2 on page 20 of the textbook, and write each pitch in ratio form.
 Answer
Answer
- Which of the three roofs in question 3 is the steepest? Why? Answer
- What implications for safety are there with roof c in comparison to the other roofs? Answer
- Answer the following.
Roofs and water slides are not the only objects where safety and functionality are related directly to slope. Examine the following photos of road signs providing information to drivers about the steepness of the road ahead. Why are these signs necessary? What purpose do they serve?

8% sign: iStockphoto/Thinkstock; runaway ramp: iStockphoto/Thinkstock; low gear: Hemera/Thinkstock
1.29. Explore 3
Section 1: Slope—Physical Objects
Read more about how road grade is calculated on page 25 of Mathworks 11. Begin at “Explore the Math.” As you read, think about these questions:
- If the slope of a roof is referred to as pitch, then what is the slope of a road referred to as?
- What is the one small difference between the slope formula and the percent grade formula?
Using an appropriate grade is not just important with roads. The comfort and safety of athletes can be affected by the way their playing fields are constructed. Playing fields of grass need a crown (high point) in the middle and should slope to the edges. The slope needs to be between 2.0% and 2.5% for the grass field to drain well.

Comstock/Thinkstock
Example
A Canadian football field is typically 65 yd wide. If the crown in the centre is 3 ft high, would the field meet the requirements for good drainage?
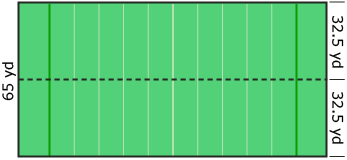
The crown of the field will be in the centre. That is half the width of 65 yd. As the illustration shows, this is 32.5 yd from the sidelines.
![]()
Remember to have the rise and run in the same units when calculating both slope and percent grade.
You may remember that 1 yd is equivalent to 3 ft. So the crown is 3 ft high or 1 yd high. Now that all measurements are in yards, finding the percent grade is simpler.
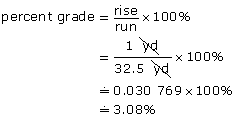
A crown of 3 ft would exceed the 2% to 2.5% range needed to have the field drain adequately.
1.30. Explore 4
Section 1: Slope—Physical Objects
Self-Check 2
The following diagram represents a ramp leading into a house. Movers will use the ramp to bring heavy boxes into the home.
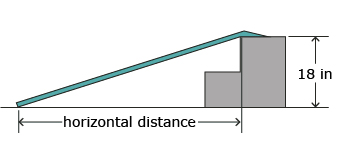
- How does having a ramp provide safety for workers? Answer
- How does the number of steps affect the ramp’s grade? Answer
- If the height (rise) of the steps is 18 in and the horizontal (run) distance is 90 in, then the slope as a percent grade of the ramp is
- 500%
- 0.2%
- 20%
- 500%
Share 2
With a partner or with a group of people, discuss the following.

bus: Photodisc/Thinkstock; wheelchair ramp: iStockphoto/Thinkstock
Wheelchair accessibility requires ramps with specific slopes. The ramp slopes are measured in percent grade. Compare the photos.
- What problems do you see with the ramp on the right? Would someone in a wheelchair be able to use this ramp without help?
- The slope of the bus floor appears to be zero, so what is the purpose of the pink strap?
![]() If required, save a copy of your discussion in your course folder.
If required, save a copy of your discussion in your course folder.
1.31. Explore 5
Section 1: Slope—Physical Objects
Read more about barrier-free spaces and ramps on page 25 of Mathworks 11. Focus on the “Math On The Job” section. As you read, think about what
- barrier-free design is
- safety features a building officer must be familiar with
- changes might be needed to make a house more functional for someone with a wheelchair
Self-Check 3
- Refer to your reading on page 25 of the textbook. Richard was asked to inspect a wheelchair ramp. Is the ramp legal? Use calculations and explain your answer. Answer
- Go to page 19 of Mathworks 11, and read “Build Your Skills” question 1.
- Go to “Build Your Skills” on page 21 of Mathworks 11, and answer question 5. Is Sarah correct, or is Amy correct? Explain why. Support your answer. Answer
It is now time to add new math terms to your Mathematics 20-3: Glossary Terms document.
In this lesson the new term you will add is
- percent grade
At this time, you may want to add the percent grade formula to your Formula Sheet.
1.32. Connect
Section 1: Slope—Physical Objects
Connect
Going Beyond
Try question 7 on page 32 of Mathworks 11. The following points should help you:
- The horizontal distance (run) is given.
- The vertical height (rise) needs to be determined from the given information.
- Convert all dimensions into inches.
Project Connection
![]() You are now prepared to begin working on Step 3 of the Module 3 Project: Luge Track Comparison. Make sure to save all your project work in your course folder to submit at the end of Section 2.
You are now prepared to begin working on Step 3 of the Module 3 Project: Luge Track Comparison. Make sure to save all your project work in your course folder to submit at the end of Section 2.
Lesson 3 Assignment
Your lesson assignment contains some problems for you to solve using knowledge gained during the lesson. Now you will have the chance to apply the concepts and strategies learned to a new situation. Show work to support your answers.
Open the Lesson 3 Assignment that you saved to your course folder and complete the questions.
1.33. Lesson 3 Summary
Section 1: Slope—Physical Objects
Lesson 3 Summary

© cris13/387842/Fotolia
In this lesson you took an in-depth look at the meaning of slope. You saw how slopes relate to the steepness of slides, roofs, roads, and ramps. You also saw that considering the slope of objects is an important safety concern. In some cases, slope can make the difference between having or not having an accessible building.
You used a variety of different means to calculate and discuss slope. The formula percentage grade = ![]() × 100% was used to describe the slope of roads and ramps. You also applied the ratio form of a slope to discuss slope in terms of roof pitch. You then used your knowledge of slope to determine which of several objects was steeper.
× 100% was used to describe the slope of roads and ramps. You also applied the ratio form of a slope to discuss slope in terms of roof pitch. You then used your knowledge of slope to determine which of several objects was steeper.
In Section 2 you will explore slope further, but not in terms of a physical object as you did in this section. You will see that slopes can also describe a rate of change.
1.34. Section 1 Summary
Section 1: Slope—Physical Objects
Section 1 Summary

© blende64/21340293/Fotolia
Snow-covered mountains likely appeal to you whether you are a skier or a snowboarder, or if you prefer to stay indoors. You can see the varying slopes of different parts of the mountains, and you can spot where avalanches have stripped away the trees.
In this section you explored slope and ways to describe slopes. You looked at the special cases of slope, such as zero slope and undefined slope. You discovered ways to give slope a number value, and you considered safety issues related to sloped objects.