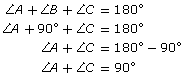Lesson 2
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-3 SS |
| Book: | Lesson 2 |
| Printed by: | Guest user |
| Date: | Tuesday, 2 December 2025, 6:58 AM |
Description
Created by IMSreader
1. Lesson 2
Module 4: The Right Kind Of Triangles
Lesson 2: Similar Right Triangles
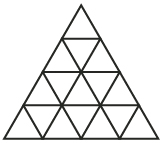
Focus
How many triangles can you see in the drawing to the right? Do you see 16, 17, 21, or more? What strategy did you use to keep track of each triangle? Did you notice that the triangles in this diagram all have the same shape? They are all similar triangles and are found in many different puzzles and games.
You may recognize the similar triangles in the following photos.

pyramid: Hemera/Thinkstock; game board: PhotoObjects/Thinkstock
In previous math courses you worked with all kinds of similar triangles. In this lesson you will focus on similar right triangles and how they can be used to solve problems.
Lesson Question
In this lesson you will investigate the following question:
- How are the relationships among the sides and angles of similar right triangles used to solve problems?
Assessment
Your assessment for this lesson may include a combination of the following:
- course folder submissions from Try This and Share
- your contribution to the Mathematics 20-3: Glossary Terms
- Lesson 2 Assignment (Save a copy of your lesson assignment to your course folder now.)
- the Project Connection
Materials and Equipment
- tape measure (metric or imperial)
- calculator
1.1. Launch
Module 4: The Right Kind Of Triangles
Launch
This section checks to see if you have the necessary background knowledge and skills required to successfully complete Lesson 2.
Launch will review the following topics:
- similar triangles
- vertically opposite angles
Complete the following Are You Ready? questions. If you have difficulty or any questions, visit Refresher for a review or contact your teacher.
1.2. Are You Ready?
Module 4: The Right Kind Of Triangles
Are You Ready?
- If the corresponding angles of two triangles are equal in measure, the triangles are similar.
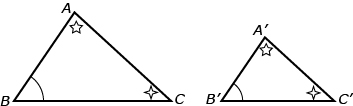
In the diagram, is similar to
is similar to  because
because 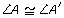 ,
, 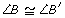 , and
, and 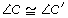 .
.
- If two triangles are similar, the ratios of the corresponding sides are equal; that is, the corresponding sides are proportional. In the diagram for question 1, what are the equal ratios? Use the two-letter names for the lengths of the sides. Answer
-
If the corresponding sides of two triangles are proportional, the triangles are similar.
In the following diagram, if
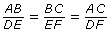 , then,
, then, 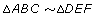 .
.
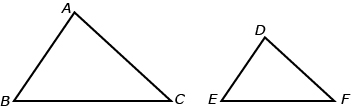
Since the triangles are similar, name the pairs of angles that are equal in measure. Answer
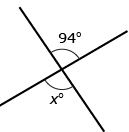
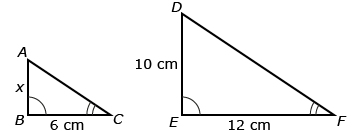
- In the diagram
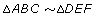 , what is the value of x? Answer
, what is the value of x? Answer
If you answered the Are You Ready? questions without problems, move on to Discover.
If you found the Are You Ready? questions to be difficult, complete Refresher to review these topics.
1.3. Refresher
Module 4: The Right Kind Of Triangles
Refresher
If you don’t know the answers in Are You Ready?, or if you require more information, do the following activities to review similar triangles and opposite angles.
Similar Triangles
|
© Nicolas McComber/shutterstock
|
Opposite Angles
|
Go back to Are You Ready?, and try the questions again. Contact your teacher if you continue to have difficulty with the questions.
1.4. Discover
Module 4: The Right Kind Of Triangles
Discover

Medioimages/Photodisc/Thinkstock
You may not have a totem pole outside your home; however, if a nearby power pole or light standard casts a shadow along a level stretch of ground on a sunny day, you can determine its height by using similar right triangles.
Try This 1
You will need a partner to help you and a measuring tape that has both SI and imperial units.
Step 1: On a sunny day, measure the length of the shadow cast by a power pole or light standard. At the same time, measure the length of the shadow cast by a vertical object of known height. The object could be a fence post, a hockey stick, or even your partner.
Step 2: Draw a diagram and record your measures. A sample diagram is shown below.
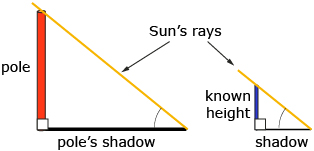
- On your diagram, describe what objects you chose and the date and time of day when you took your measurements.
- Explain why the Sun’s rays shown in the diagram must strike the ground at the same angle in each triangle.
- Explain how you know the two right triangles are similar.
- Set up a proportion and solve for the height of the pole.
![]() Save your responses to your course folder.
Save your responses to your course folder.
Share 1
Share your responses to the questions in Try This 1 with a classmate or with a group of people.
How are your responses to the questions similar? How do your answers differ?
1.5. Explore
Module 4: The Right Kind Of Triangles
Explore
In Discover, the two right triangles you used were similar because one pair of acute angles were equal in measure.
Suppose you had two right triangles, ![]() , and in those triangles
, and in those triangles ![]() . Then,
. Then, ![]() .
.
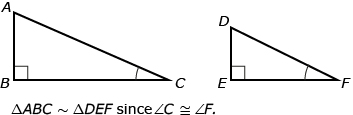
The reason is based on the principle that in a right triangle, the two acute angles must add up to 90°.
| For |
|
Because angle B is equal to 90°,
the two acute angles, A and C, must also equal 90°. |
|
| For example, if ∠C = 40°, then ∠A must be 50°. | 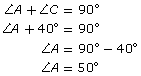 |
| Since the two triangles are similar, the corresponding angles will be the same. |
∠F = 40° and ∠D = 50° |
Try This 2
Jonathan walked 15 m from the wall of his apartment building. At that point, he noticed that his shadow reached the same point on the ground as the building’s shadow. If Jon is 1.6 m tall, and his shadow is 3 m long, how high is the apartment building? Round your answer to one decimal place.
- Sketch and label a diagram to represent the problem.
Watch the steps involved in solving this problem in the Apartment Shadow Problem. On the final slide of the animation, you will set up the proportion needed to solve this problem.
- Solve the proportion to find out how high the apartment building is.
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.6. Explore 2
Module 4: The Right Kind Of Triangles
Example
A roof truss is built with a slope of 2.5:12. What is the vertical height of the truss in the diagram? Round your answer to one decimal place.
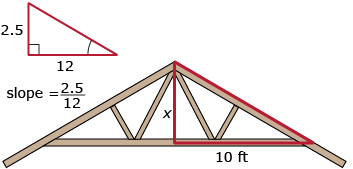
Solution
The two right triangles representing the slope and the truss are similar because the truss must have the same slope. Corresponding sides will have the same ratios and, therefore, all the angles will be equal.
Let x be the height of the truss.
Set up a proportion for the corresponding sides of the triangles. |
|
Solve the proportion.
The height is approximately 2.1 ft or 2 ft 1 in. |
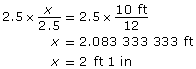 |
Self-Check 1

iStockphoto/Thinkstock
- A wheelchair ramp is 30 m long, and its bottom is 1.5 m below the top of the ramp.
- How far is a wheelchair above the foot of the ramp when it is 10 m from the top of the ramp? Answer
- What is the slope of the ramp? Round your answer to two decimal places. Answer
- How far is a wheelchair above the foot of the ramp when it is 10 m from the top of the ramp? Answer
- Vanaja is standing on the east bank of the South Saskatchewan River in Saskatoon. She looks at the historic Bessborough Hotel on the opposite shore and wonders how far away the building is. Vanaja walks 150 m downstream along the bank and stops and places a stick, S, in the bank. Then she walks 30 m further downstream. She turns 90° and walks 20 m away from the river until she sees that the stick she placed on the bank lines up with the hotel across the river. Calculate the original distance, x, that Vanaja was from the hotel.
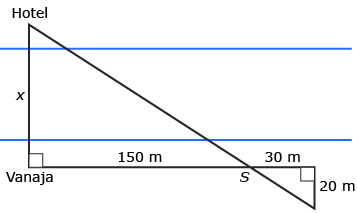
Answer
- A timber is positioned 30 cm from the end of a 2-m steel bar. The free end of the bar is lifted 20 cm. To the nearest centimetre, how high is the timber off the ground?
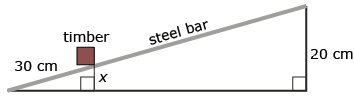
Answer
- The foot of a 20-ft ladder is located 5 ft from a vertical wall. A painter is standing 16 ft above the foot of the ladder. How far from the wall is he?

iStockphoto/Thinkstock
Answer
1.7. Explore 3
Module 4: The Right Kind Of Triangles
Self-Check 2
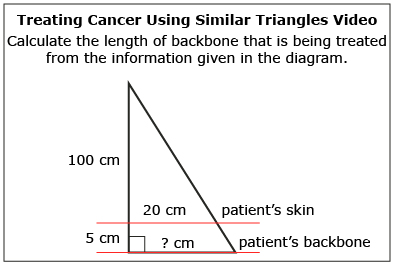
Similar triangles have many real-life applications, including precise measurements for the treatment of diseases. Search the Internet for a video about treating cancer using similar triangles. Use the search term “video similar triangles and radiation therapy.”
From the information provided in the video, calculate the length of backbone that is being treated in the diagram provided below. Answer
It is now time to add new math terms to Mathematics 20-3: Glossary Terms.
In this lesson the new terms you will add are
- similar triangles
- congruent angles
1.8. Connect
Module 4: The Right Kind Of Triangles
Connect
Going Beyond
This puzzle involves deductive reasoning and some knowledge of similar triangles and slope.
Print two copies of this Missing Square Puzzle. The two triangles appear to be identical—the base of each triangle is 13 units and the height of each one is 5 units. To convince yourself that each triangle is made up of identical pieces, cut out the pieces from the upper triangle in one copy that you printed. Then fit the pieces from the top triangle onto the bottom triangle in your other copy.
Where does the missing square come from?
Lesson 2 Assignment
Your lesson assignment contains some problems for you to solve using the knowledge gained during the lesson. Now you will have the chance to apply the concepts and strategies that you have learned to a new situation. Show your work to support the answers.
Open the Lesson 2 Assignment that you saved to your course folder and complete the questions.
1.9. Lesson 2 Summary
Module 4: The Right Kind Of Triangles
Lesson 2 Summary
How many similar triangles can you see in this drawing? How many are right triangles?
In this lesson you saw many similar right triangles. You reviewed their properties and found that if two right triangles had one acute angle with the same measurement, then the right triangles were similar. You also used similar right triangles to solve a variety of problems.