Lesson 3
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-3 SS |
| Book: | Lesson 3 |
| Printed by: | Guest user |
| Date: | Tuesday, 2 December 2025, 7:05 AM |
Description
Created by IMSreader
1. Lesson 3
Module 4: The Right Kind Of Triangles
Lesson 3: Trigonometry Review
Focus

National Capital Commission
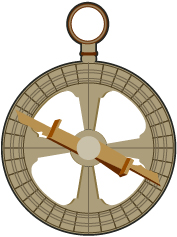
At Nepean Point in Ottawa, there is a statue of Samuel de Champlain, the seventeenth-century French explorer, mapmaker, and “father of New France” (Québec). Champlain is shown holding an astrolabe. An astrolabe is an instrument used by mariners to determine location. An astrolabe is used to measure angles of elevation of the Sun or the North Star. From these measurements, and using mathematical tables based on trigonometry, the user could determine latitude or time. The astrolabe is an ancient form of GPS.
The mathematics of trigonometry is even more important to Canadian society today than it was four centuries ago. In this lesson you will review the basic concepts of right-triangle trigonometry. You explored these concepts in previous mathematics courses.
By the way, if you look carefully at de Champlain’s statue, you will notice he is holding the astrolabe upside down.
Lesson Questions
In this lesson you will investigate the following questions:
- How is right-triangle trigonometry applied in problem situations?
- What is the relationship between slope, angle of elevation, and the tangent ratio?
Assessment
Your assessment for this lesson may include a combination of the following:
- course folder submissions from the Try This and Share sections of the lesson
- your contribution to the Mathematics 20-3: Glossary Terms
- Lesson 3 Assignment (Save a copy of your lesson assignment to your course folder now.)
Materials and Equipment
- stiff paper or cardboard the size of printer paper
- scissors
- tape
- glue stick
- drinking straw
- a weight (such as a bolt or large washer)
- 30 cm of strong thread or fishing line
- tape measure (metric or imperial)
- calculator
1.1. Launch
Module 4: The Right Kind Of Triangles
Launch
This section checks to see if you have the necessary background knowledge and skills required to successfully complete Lesson 3.
Launch will review the following topics:
- basic trigonometry terminology
- using a calculator with the trigonometric functions
- angles of elevation and depression
Complete the following Are You Ready? questions. If you have difficulty or any questions, visit Refresher for a review or contact your teacher.
1.2. Are You Ready?
Module 4: The Right Kind Of Triangles
Are You Ready?
Before doing any trigonometric calculations, you must make sure that your calculator is in degree mode. Refer to the user manual or ask your teacher if you are not sure how to check.
- Identify the hypotenuse, opposite, and adjacent sides in right triangles in Exploring Trigonometry Interactive.
- Define angles of elevation and angles of depression. Answer
- Answer the following questions. Round to four decimal places. Make sure your calculator is in degree mode.
- Answer the following questions. Round to the nearest degree. Make sure your calculator is in degree mode.
1.3. Refresher
Module 4: The Right Kind Of Triangles
Refresher
If you don’t know the answers in Are You Ready?, or require more information, review these topics.
Opposite Side (Right Triangle) |
|
Using a Calculator with the Trigonometry Functions
|
tan 34° =
tan θ = 1.2743
|
Angle of Elevation |
Go back to Are You Ready? and try the questions again. Contact your teacher if you continue to have difficulty with the questions.
1.4. Discover
Module 4: The Right Kind Of Triangles
Discover
In this section you will make and use a clinometer. A clinometer can be used to measure angles of elevation and depression. If you happen to have a clinometer from a previous mathematics course, feel free to use it.
Try This 1
Work with a partner or with a group to complete this activity. You will need the following materials:
- stiff paper or cardboard the size of printer paper
- scissors
- tape
- glue stick
- drinking straw
- a weight (such as a bolt or large washer)
- 30 cm of strong thread or fishing line
- tape measure
Follow Steps 1 through 5 in the instructions from Lesson 1 of Mathematics 10-3: Module 7 to create your clinometer.
Now, use your clinometer to determine the height of a tall object, such as a tree or a flag pole.
Step 6: Select a tall object standing on level ground.
Step 7: Choose a convenient spot on the ground near the tall object. Make sure that this spot is level with the base of the object you chose. Measure the distance from this spot to the object using a tape measure.
Step 8: With the help of a partner, use your clinometer to measure the angle of elevation to the object's top from this position.
Step 9: Measure the height of your eye where you took the measurement.
Step 10: Sketch and record your measurements on a diagram similar to the following.
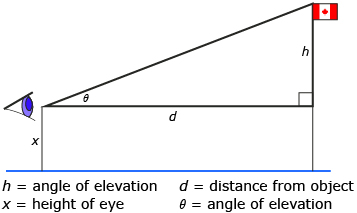
Now, answer the following questions:
- What object did you choose?
- Substitute your measurements into the formula
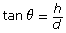 to determine how high the top of the object is above eye level.
to determine how high the top of the object is above eye level.
- Determine the total height of the object.
- Did you round your answer? If so, why?
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.5. Explore
Module 4: The Right Kind Of Triangles
Explore
In Discover you may have noticed that you used the tangent ratio to determine the height of a tall object. Later in this lesson you will become aware of the relationship between the tangent ratio and angles of elevation and depression.
You may recall from previous mathematics courses that there are three basic trigonometric ratios:
- tangent ratio
- sine ratio
- cosine ratio
If θ is the measure of an acute angle of a right triangle, the sides in reference to this angle would be labelled as shown in the diagram. The sine, cosine, and tangent ratios for θ are also shown.
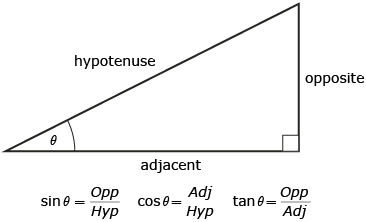
The memory aid SOH-CAH-TOA can be used to help remember these ratios.
Sin is Opposite over Hypotenuse; Cos is Adjacent over Hypotenuse; Tan is Opposite over Adjacent.
Try This 2
Work through Exploring Trig Ratios – Use It to review how the trigonometry ratios are used to calculate missing sides and angles.
1.6. Explore 2
Module 4: The Right Kind Of Triangles
Self-Check 1
- Determine the value of x. Round to one decimal place.
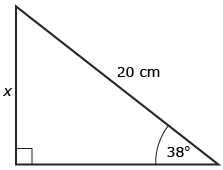
Answer
- Determine the value of θ. Round to the nearest degree.
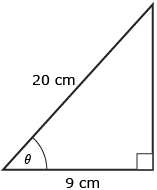
Answer
Next, you will apply the trigonometric ratios in various problem situations. In Try This 3 you will explore the relationship between slope, angle of elevation, and the tangent ratio.
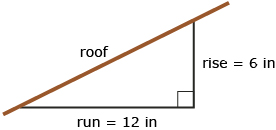
Try This 3
In areas of Canada with high snowfall, the minimum pitch (slope) for new construction is 6:12, which is said “six twelve.” To the nearest degree, what angle of elevation does the roof make with the horizontal?

iStockphoto/Thinkstock
- A pitch or slope of 6 to 12 means the roof rises 6 in to a run of 12 in. Use this information to sketch and label a diagram.

- Use the slope formula to find the slope of the roof.

- In the diagram, label the angle of elevation as θ.
- Label the adjacent, opposite, and hypotenuse sides in reference to the angle of elevation.
- Choose the correct trig ratio to help find θ, the angle of elevation.

- Compare the tangent ratio you found in question 5 to the slope ratio you found in question 2. What do you notice?
- Continue to solve for θ.

Share 1
Discuss the following question with a partner or with a group of people:
- Based on question 6 from Try This 3, how would you explain the relationship between slope, angle of elevation, and the tangent ratio?
Create a short paragraph to explain this relationship.
1.7. Explore 3
Module 4: The Right Kind Of Triangles

Digital Vision/Thinkstock
You discussed angle of elevation with your partner in Share 1. Here is an example of solving a problem involving an angle of elevation.
Example
A hot-air balloon is 100 m higher than an observer on the ground. From the observer’s vantage point, the angle of elevation of the balloon is 37°. What is the straight-line distance from the observer to the balloon? Round your answer to the nearest metre.
Solution
Draw and label a diagram. Let x be the distance from the balloon to the observer.
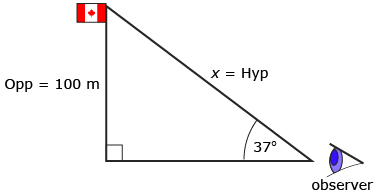
From SOH-CAH-TOA, sine is the appropriate ratio.
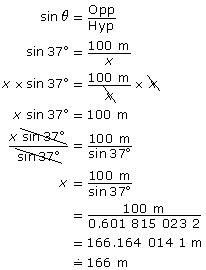
The balloon is approximately 166 m from the observer.
Example
When Canada’s first transcontinental railroad was completed in 1885, the highest point on the line was at Kicking Horse Pass near Field, British Columbia. For trains headed west through the pass, there was a dangerous descent to the foot of Mt. Stephen. There the grade was 4.5%, which was more than four times the usual grade. The steep grade on Mt. Stephen, referred to as the Big Hill, led to numerous accidents.

iStockphoto/Thinkstock
A grade (slope) of 4.5% means the rail line rises 4.5 m for every 100 m it travels horizontally. With this grade, what is the angle that the rail line is inclined to the horizontal? Round your answer to the nearest tenth of a degree.
Solution
Sketch and label a diagram. Let θ be the angle of elevation.
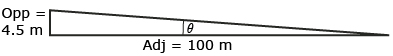
From SOH-CAH-TOA, tangent is the appropriate ratio.

The angle that the rail line is inclined to the horizontal is approximately 2.6°.
1.8. Explore 4
Module 4: The Right Kind Of Triangles

iStockphoto/Thinkstock
Self-Check 2
- An airplane being flown at a vertical height of 100 m is approaching the runway of the local airport. From the cockpit, the angle of depression to the start of the runway is 5°. To the nearest 10 m, calculate the horizontal distance between the plane and the start of the runway. Answer
- A 16-ft ladder rests against a building and makes an angle of 76° with the ground. How far is the foot of the ladder from the wall? Round your answer to one decimal place. Answer
- At noon in Whitehorse on June 21, a 5-m flagpole cast a 3.5-m shadow. To the nearest degree, what was the angle of elevation of the Sun? Answer
- A loading ramp makes an angle of 20° with the ground. One end of the ramp rests on the ground. The other end leans against a storage platform that is 1 m high. How long is the ramp? Round your answer to one-tenth of a metre. Answer
- Think back to the Kicking Horse Pass from the previous example. The Big Hill line had to be replaced. By 1909 the CPR, using a design from engineer John Schwitzer, completed a pair of spiral tunnels that reduced the grade to 2.2%. Each spiral tunnel makes a three-quarter turn. The lower tunnel was constructed under Mt. Ogden, and the upper tunnel was made under Cathedral Mountain.

© Parks Canada
The upper tunnel under Cathedral Mountain is inclined at 0.983° to the horizontal. The change in elevation is 17 m. To the nearest metre, what is the length of this tunnel? Answer
It is now time to add new math terms to Mathematics 20-3: Glossary Terms.
In this lesson the new terms you will add are
- opposite side
- adjacent side
- angle of elevation
- angle of depression
1.9. Connect
Module 4: The Right Kind Of Triangles
Connect

iStockphoto/Thinkstock
Going Beyond
If you're at a second-storey window or balcony, you can use your clinometer to determine the height of the window you are looking through. You can also measure a nearby tall object, such as a building, a tree, or a flagpole. You will also need a tape measure and your calculator.
Step 1: Use your tape measure to determine the horizontal distance from the window to the tall object.
Step 2: From the window or balcony, first measure the angle of elevation to the object's top. Then, measure the angle of depression to the object's bottom.
Step 3: To determine the height above ground of your window and the height of the tall object, answer the following questions.
- Identify the object you chose.
- Draw a diagram similar to the following one. Record the measurements.
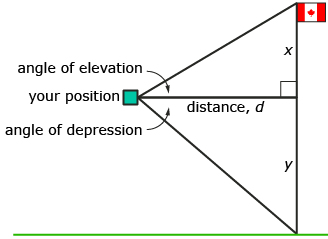
- Determine x, y (the height of your window), and the total height of the object.
Lesson 3 Assignment
Your lesson assignment contains some problems for you to solve using knowledge gained during the lesson. Now you will have the chance to apply the concepts and strategies learned to a new situation. Show work to support your answers.
Open the Lesson 3 Assignment that you saved to your course folder and complete the questions.
1.10. Lesson 3 Summary
Module 4: The Right Kind Of Triangles

David Hiller/Photodisc/Thinkstock
Lesson 3 Summary
The astrolabe used by Samuel de Champlain and the transit used by surveyors make use of very similar mathematics. Both use trigonometry and right angles to find locations.
People who work in other trades use trigonometry as well. These trades include electricians, road builders, carpenters, and plumbers. Check to see what type of mathematics is used in your chosen occupation.
In this lesson you reviewed right-triangle trigonometry and its application. One application included the slope—sometimes called gradient, pitch, or grade depending on the person applying slope on the job.