Lesson 3
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-3 SS |
| Book: | Lesson 3 |
| Printed by: | Guest user |
| Date: | Tuesday, 2 December 2025, 6:58 AM |
Description
Created by IMSreader
1. Lesson 3
Module 6: Surface Area
Lesson 3: Working with Formulas for Surface Area
Focus

iStockphoto/Thinkstock
Spherical tanks are often used to store volatile petroleum products. One advantage of a spherical tank is that it minimizes the surface area for a given volume, which in turn minimizes the transfer of heat from the outside of the tank to its contents. Another advantage of this design is that spherical tanks have no built-in weak spots; the pressure from the contents is distributed equally across the tank’s interior, making this design ideal for high-pressure storage.
In this lesson you will explore formulas for determining surface areas of various geometric shapes, including spheres, and you will apply these formulas to solve a variety of real-world problems.
Lesson Questions
- What are the common formulas for surface area, including the formula for the sphere?
- How can surface area formulas be manipulated to solve for other dimensions?
Assessment
Your assessment for this lesson may include a combination of the following:
- course folder submissions from the Try This and Share sections of the lesson
- your contribution to the Mathematics 20-3: Glossary Terms and the Formula Sheet
- Lesson 3 Assignment (Save a copy of your lesson assignment to your course folder now.)
Materials and Equipment
- calculator
1.1. Launch
Module 6: Surface Area
Launch
This section checks to see if you have the necessary background knowledge and skills required to successfully complete Lesson 3.
Complete the following Are You Ready? questions. If you have difficulty or any questions, visit Refresher for a review or contact your teacher.
1.2. Are You Ready?
Module 6: Surface Area
Are You Ready?
In previous mathematics courses, you found the areas of various two-dimensional shapes using the following formulas. Not only did you use these formulas to find areas, you used them to find a missing dimension if you knew the area.

Find the missing dimension in each of the following questions.
- The square area of the top of a sugar cube is 0.25 in2. How long is each edge? Answer

iStockphoto/Thinkstock
- According to the building code in Calgary, the minimum area for a basement bedroom window is 0.35 m2. If a rectangular window is 70 cm long, what is the minimum width the window can have? Answer

iStockphoto/Thinkstock
- The area of a circular utility-hole cover is 0.385 m2. To the nearest centimetre, what is the diameter? Answer

iStockphoto/Thinkstock
If you answered the Are You Ready? questions without any issues, move on to Discover.
If you had some difficulty with the Are You Ready? questions, complete Refresher.
1.3. Refresher
Module 6: Surface Area
Refresher
If you don’t know the answers in Are You Ready?, or if you require more information, work through the following activities to review square roots and area formulas.
 |
Square Root
|
|
© 2007 Copeman Photography |
Area Formulas
|
Go back to Are You Ready? and try the questions again. Contact your teacher if you continue to have difficulty with the questions.
1.4. Discover
Module 6: Surface Area
Discover
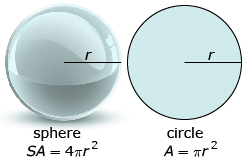
In this Discovery you will investigate the relationship between the area of a circle and the surface area of a sphere.
Try This 1
Click the button on the left to open Investigation: Area of a Circle and Surface Area of a Sphere.
![]() Save a copy of your answers in your course folder.
Save a copy of your answers in your course folder.
Share 1
With a classmate or a group of people, share your responses to the investigation questions from Try This 1. How do your formlas for the surface area of a sphere compare? Once you have compared answers, discuss the following question:
- What is the relationship between the area of a circle and the surface area of a sphere with the same radius?
![]() If required, save a copy of your discussion to your course folder.
If required, save a copy of your discussion to your course folder.
1.5. Explore
Module 6: Surface Area
iStockphoto/Thinkstock
Explore
In Discover, you developed the formula for the surface area of a sphere and found that the surface area is exactly 4 times the area of a circle with the same radius.
In Explore, you will apply surface area formulas to solve a variety of problems. You will also manipulate these formulas to calculate dimensions of three-dimensional objects when given the surface area.

Photos.com/Thinkstock
Archimedes of Syracruse (287–212 BCE) was one of the greatest mathematicians and inventors of all time. Legend has it that he leapt from his bath crying “Eureka” (Greek for “I discovered it”) when he realized that the buoyancy of submerged objects could be used to determine whether the King of Syracruse’s crown was pure gold.
A brilliant and inventive mind, Archimedes considered his work with the sphere, including a proof of the formula for its surface area, his greatest accomplishment.
The following example gives you an opportunity to use the formula for the surface area of a sphere that you determined in Discover.
Example

iStockphoto/Thinkstock
An NBA basketball is approximately 24 cm in diameter. What is the surface area? Round your answer to the nearest cm2.
Solution
The diameter of the ball is 24 cm, but you need the radius for the surface area formula.
The radius, r, is equal to 24 cm ÷ 2, or 12 cm.
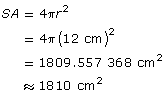
The surface area of the basketball is approximately 1810 cm2.
1.6. Explore 2
Module 6: Surface Area
Self-Check 1

Hemera/Thinkstock
In previous mathematics courses, you explored several formulas for surface area. These formulas included the surface areas of cubes, rectangular prisms, cones, and cylinders. The following chart summarizes these formulas. You may find these formulas helpful for the following problems.
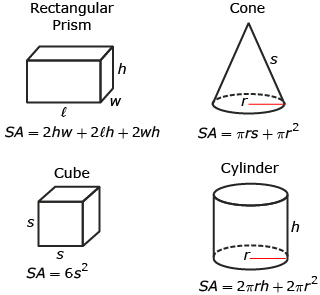

Hemera/Thinkstock
Air vents, climate-control ducts, roofing, siding for houses, machinery, traffic and warning signs, car bumpers, railway cars, manufacturing equipment, and many other items use sheet metal. Workers are given a certain surface area and may be asked to determine maximum dimensions with an allotted amount of sheet metal.
Manipulating surface area formulas is a useful concept for sheet-metal workers.
Try This 2
Ross, a sheet-metal worker, makes a closed rectangular duct that is 32 in long, 15 in wide, and 16 in high, as shown.
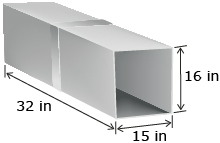
- Draw a net of the duct. How many sides does the net have?

- Calculate the area of each side in the net.

- Since there are no ends to the duct, how would you change the formula for the surface area of a rectangular prism to find the surface area for this duct?

- Ross has the same amount of metal as you calculated in question 2. He is to make a duct that is also 32 in long, but that has a width of 8 in. Sketch a net of the duct Ross is to fabricate.
- Calculate the height of the new duct.


![]() Save all your work and calculations from Try This 2 in your course folder.
Save all your work and calculations from Try This 2 in your course folder.
1.7. Explore 3
Module 6: Surface Area
In the next example, you will see one way that the formula for surface area of a sphere can be manipulated. Even though the formula has r2 in it, you can find a value for the variable r.
Example
A cube is 2 in on each side. To the nearest tenth of an inch, what is the diameter of a sphere with the same surface area? ![]()
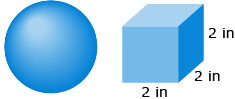
Solution
First, determine the surface area of the cube.
Each side of the cube (s) is 2 in. |
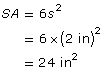 |
| Since the sphere has the same surface area as the cube, substitute the 24 in2 into the surface area formula for a sphere. |  |
The question asks for the diameter of the sphere.
The diameter is twice the radius. Therefore, the diameter of the sphere is about 2.8 in. |
2 × 1.4 in = 2.8 in |
Example

iStockphoto/Thinkstock
Dowels are small, cylindrical pieces of wood that fit into holes at the joint of two larger pieces of wood to add stability to the joint. Using dowels to fasten wood works well in making shelves, cabinets, and small pieces of wooden furniture.
- A cylindrical dowel is 0.25 inches in diameter and its length is 1 in. To keep the dowel in place, glue is spread over its entire surface. What is the surface area of each dowel, to the nearest hundredth of an inch?
- How long would a dowel with the same diameter be if its surface area was exactly 2 in2? Round your answer to the nearest hundredth of an inch.
Solution
Click the button on the left to watch the “Cylindrical Dowel Solution” to see a possible way to solve this problem.
1.8. Explore 4
Module 6: Surface Area
Self-Check 2
- A conical paper cup has a slant height of 10 cm. The amount of paper needed to manufacture this cup depends on its surface area, which is 110 cm2. To the nearest tenth of a cm, calculate the radius of the paper cup.
 Answer
Answer

iStockphoto/Thinkstock
- Turn to page 135 of “Extend Your Thinking” in MathWorks 11, and do question 6. Answer
It is now time to add new math terms to Mathematics 20-3: Glossary Terms.
In this lesson the new term you will add is
- sphere
1.9. Connect
Module 6: Surface Area
Connect
Lesson 3 Assignment
Your lesson assignment contains some problems for you to solve using knowledge gained during the lesson. Now you will have the chance to apply the concepts and strategies that you have learned to a new situation. Show work to support your answers.
Open the Lesson 3 Assignment that you saved to your course folder and complete the questions.
1.10. Lesson 3 Summary
Module 6: Surface Area
Lesson 3 Summary

Hemera/Thinkstock
Hopper-style grain bins are cylindrical with conical tops and bottoms. After this lesson you should be able to calculate the amount of material used in their construction. The amount of material is a function of surface area.
In this lesson you explored surface area formulas and their application in a variety of practical problem situations.